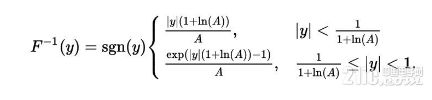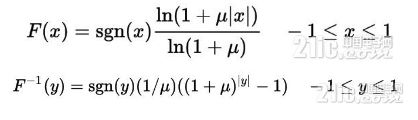这么讲音频算法,真是人人都能懂
这一章开始介绍一些算法相关的内容.前面有几章对播放强调较多,这期本来想写录音方面的内容.但是普通的麦克风电路主要是模拟电路,独立做一章来写觉得内容有点少,所以会在其他章节穿插介绍.至于MEMS麦克风,因为涉及到PDM解码,可以在后面做独立一章来写.
点击链接加入群【嵌入式音频信号处理】:https://jq.qq.com/?_wv=1027&k=45wk8Ks
嵌入式音频专用资料代码分享:https://pan.baidu.com/s/1dFh5pWd
本期活动地址:-pls wt
---
前言
本章这里说的算法,主要是指的编码解码的算法,就是所谓的CODEC(Encode/Decode).语音识别,语音合成,环境音效等技术属于另外不同的算法,这些算法主要针对原始(raw)的音频数据进行.而在实际工程实践中,编解码算法是研究的最多的内容.原因以前也说过,原始音频内容太多,对存储传输的带宽要求过大,而音频数据本身又有相当大的冗余,故此这一方面的研究可以说在个人电脑诞生之前就开始了.早期的电信行业与计算机行业属于不同的两个行业,电信行业资格要老些.电报,电话,广播这些技术在一次世界大战之前就应用很广泛了.当然真正跟现代电信业有直接关系的技术则是二战之后才迅速发展的.
简介: ITU音频标准G711
ITU(国际电信联盟)是由国际电报联盟发展而来的一个国际组织,1865年在法国巴黎创建. 1947年成为联合国的一个下属机构,总部设在日内瓦.主要从事电信行业的各种技术的标准化,推进等活动.大概跟ISO,IEC,EIA,IEEE这些机构齐名.其中负责标准制定的机构原称做CCITT,1993改名为ITU-T.近几年因为呼吁加强互联网管制而跟各大垄断公司,强权国家发生了一些争吵.不过这跟本文没有啥关系,只是说到ITU,带一笔交代一下.
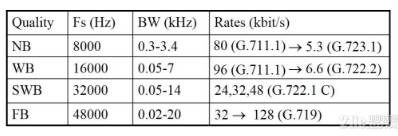
关于音频算法,ITU出了很多标准,主要着重于语音领域,因为ITU老本行就是研究电话语音传输的.因为ITU发布的语音算法标准很多,一一介绍就有点过于繁琐.所以挑一两个出来介绍,其余的标准感兴趣的读者可以自行研究.这里先给出一个概览,ITU对于标准化的音频算法,是按照带宽来分类的:
图 ITU音频算法分类
NB就是NarrowBand,即窄带
WB就是WideBand,即宽带
SWB就是SuperWideBand,即超宽带
FB就是FullBand,即全带宽
这些所谓的宽与窄都是约定俗成的,从采样率,编解码的算法等角度综合衡量的.
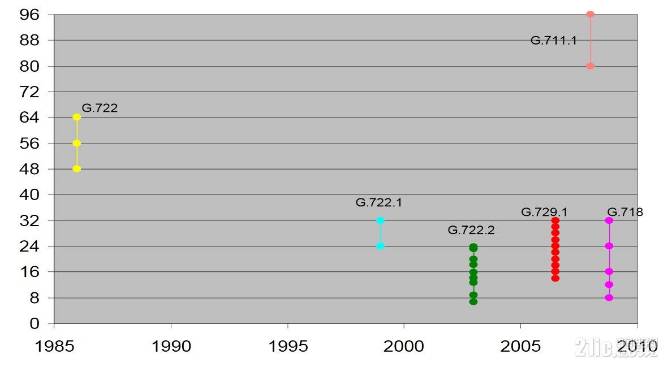
图 ITU窄带音频算法标准
图 ITU宽带音频算法标准
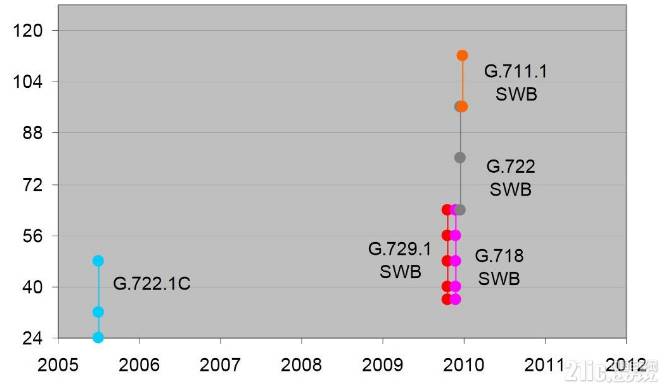
图 ITU超宽带音频算法
对于全带宽,目前只有G.729. 某些标准算法有多个版本,分属不同带宽需求类型. 这一大波算法中,G711属于历史最悠久的.本文主要介绍G711,计划后面文章还写一个G726.其余算法暂时不打算专门分出章节来写.
G711的内容是将14bit或者13bit采样的PCM音频数据编码成8bit的数据流,播放的时候将此8bit的数据还原成14bit或者13bit进行播放.不同于MPEG这种对整体或者一段音频数据进行考虑再进行编解码的做法,G711是波形编解码算法,就是一个sample对应一个编码.所以压缩比是固定的,为
8/14 = 57% (uLaw)或者
8/13 = 62% (aLaw).
因为主要用于语音音频,采样率一般使用8KHz,这样带宽为8bit乘以8KHz = 64Kbps.这个64Kbps也常常被称作"一路数字电话"作为非正式的带宽计算单位.
之所以取这些看起来比较低端的参数,是因为早期硬件能力有限,且此技术当初主要用于电话语音传输所致.G711是1972年制定的标准,专利早就过期了,所以现在属于Public Domain的内容,任何人都能任意使用.
G711主要的两种版本称之为uLaw(u律,14bit版本)与ALaw(a律,13bit版本).
uLaw主要用于日本和北美地区,除了日本和北美地区世界上基本上所有地方都用ALaw.从技术的角度来讲, ALaw因为提供了更大的动态范围,同时对硬件要求高一点.uLaw则对音量较低的信号提供更好的量化分辨率.一般来讲,如果两个国家的数字电话对接,如果有一方使用A-Law,另一方使用u-Law,那么就会采用A-Law.
有人会问,直接将14bit和13bit的PCM采样进行移位,丢掉低位得到8bit结果,岂不是更简单.但是音频数据的特点不适合这样的线性编码,直接移位的结果会丢弃音频的主要变化的部分(低位部分)从而导致直接移位的结果是音频质量大大降低.不管是ALaw还是uLaw,其核心思想是,音频的大多数变化发生在整个动态范围的低部分.而且人耳对音频幅度的感觉成对数关系.从这个角度来讲,说G711是前PC时代的MP3算法也有点道理.
下面分别介绍两种版本算法的详细情况.
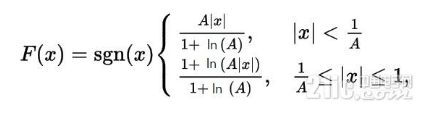
A-Law详解
A-Law的编码公式如下:
其中x为输入,F(x)为编码结果,A为压缩参数一般取值为87.6 .
A-Law解码公式,也就上述函数的反函数如下:
其中y为上述函数的结果编码.
现在动手来做一个编码与解码的程序来观察一下子整个过程.Python 3脚本.
【验证】1:ALaw算法分析验证
# ALaw Encode Decode Test
# Author: zhanzr21 @ 21ic BBS
#
# If you just want to do G711 A-Law encode/decode, use the audioop package,
# This is just for analysis and study of the algorithm itself.
#
import math
#Byte format test
LineData =[i for i in range(-4096,4096)]
#normalization
NormaData = [i/4096 for i in LineData]
A = 87.6
A_1 = (1/A)
f_test = open('g711_alaw_test.csv',mode='w')
for x in NormaData:
#Encode
if(abs(x)
y = A*abs(x)/(1+math.log(A))
y = math.copysign(y, x)
elif((abs(x)<=1) and (abs(x)>=A_1)):
y = (1+math.log(A*abs(x)))/(1+math.log(A))
y = math.copysign(y, x)
else:
#Should not come here
print("ErrorEn %f", x)
yQ = (int(y*128))/128
res = 0
resQ = 0
#Decode
if(abs(y)<(1/(1+math.log(A)))):
res = abs(y)*(1+math.log(A))/A
res = math.copysign(res, y)
elif((abs(y)<=1) and ( abs(y)>=(1/(1+math.log(A))) ) ):
res = math.exp(abs(y)*(1+math.log(A))-1)/A
res = math.copysign(res, y)
else:
#Should not come here
print("ErrorDe %f", y)
#Decode(Quantization)
if(abs(yQ)<(1/(1+math.log(A)))):
resQ = abs(yQ)*(1+math.log(A))/A
resQ = math.copysign(resQ, yQ)
elif((abs(yQ)<=1) and ( abs(yQ)>=(1/(1+math.log(A))) ) ):
resQ = math.exp(abs(yQ)*(1+math.log(A))-1)/A
resQ = math.copysign(resQ, yQ)
else:
#Should not come here
print("ErrorDeQ %f", yQ)
#for debug
f_test.write('%f,%f,%f,%f,%fn' % (x, y, yQ, res, resQ))
f_test.close()
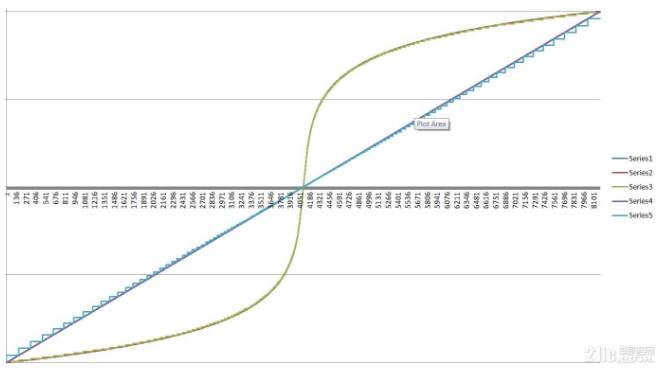
将结果画成图表以便观察(Excel):
图 从-1至1的PCM数据的ALaw编解码曲线
其中:
Series1为原始13bit的PCM采样数据[-4096,4096),归一化到[-1,1)的范围
Series2为连续编码
Series3为量化后的编码,可以看出在信号幅度高时误差较大
Series4为连续解码结果几乎没有失真
Series5为量化编码的解码结果,幅度大的时后误差较大
可以看出ALaw对0附近的数据的编码分辨率较高,而对于幅度较大的信号则分辨率较低.当然,实际使用的的时候,不管什么语言都有现成的库函数可供调用,这是个非常常见的算法.对于Python而言,使用audioop库函数(https://docs.python.org/3/library/audioop.html)即可.对于C/C++,ITU给出了参考代码,本文后面会进一步说明.
u-Law详解
uLaw的编解码公式分别如下:
其中u通常取值255.
还是动手来做一个编码与解码的程序来观察一下子整个过程.Python 3脚本.
【验证】2:uLaw算法分析验证
# uLaw Encode Decode Test
# Author: zhanzr21 @ 21ic BBS
#
# If you just want to do G711 u-Law encode/decode, use the audioop package,
# This is just for analysis and study of the algorithm itself.
#
import math
#Byte format test
LineData =[i for i in range(-4096,4096)]
#normalization
NormaData = [i/4096 for i in LineData]
U = 255
U_1 = (1/U)
f_test = open('g711_ulaw_test.csv',mode='w')
for x in NormaData:
#Encode
y = math.log(1 + U*abs(x))/math.log(1 + U)
y = math.copysign(y, x)
yQ = (int(y*128))/128
res = 0
resQ = 0
#Decode
res = U_1*((1+U)**abs(y) - 1)
res = math.copysign(res, y)
#Decode(Quantization)
resQ = U_1*((1+U)**abs(yQ) - 1)
resQ = math.copysign(resQ, yQ)
#for debug
f_test.write('%f,%f,%f,%f,%fn' % (x, y, yQ, res, resQ))
f_test.close()
这个代码比ALaw的代码要简单一些,但是因为有中间结果的幂函数运算,对硬件的要求要严格一些的.
图 uLaw的编解码数据曲线
此图与ALaw的类似,只是因为原始采样多了1bit,故此数据多了一倍.本贴的共享目录中有所有脚本与实验数据,感兴趣的同学可以下载到电脑上仔细品味一番.与ALaw相同,此处的代码仅为研究内部信号过程,实际使用中有现成的库函数可用(从标准符合度,优化度等方面考虑).
在电脑上制作/验证G711数据
两种方式,一种使用工具制作,一种使用程序来编码.实际工作当中当然使用工具制作,用程序来编码是为了验证我们对算法的理解.工具还是老熟人:Audacity.
【实验】1:Audacity操作转音频
打开一个2ch/16bit的音频文件.
图 原始16bit/2ch/11.025K的音频文件
为了更清楚理解,我们把它处理成单通道8K,16bit的数据,具体之前的章节讲过,也不赘述.结果是这样的.
点File/Export Audio在格式中选择ALaw/uLaw分别导出两个文件出来.
这样,制作就完成了,我们可以先重新打开工具,导入这两个文件看看波形试听一下子以验证上述操作无误.
图 导入的时候选格式
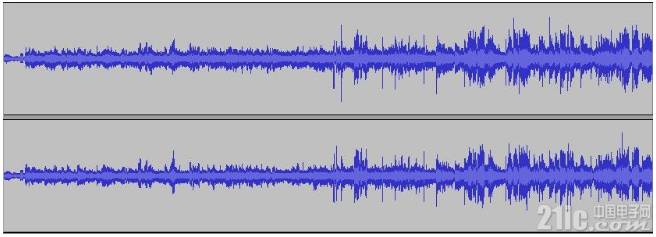
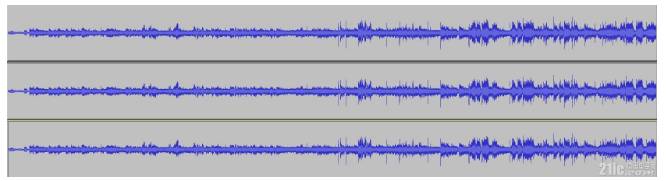
图 从上到下分别是ALaw还原,uLaw还原,原始16bit的PCM波形,肉眼看不出差别来的.后面我们会用程序来计算SNR.
至于文件大小,原始文件是1100248 bytes, 两个G711编码的文件都是550124 bytes.压缩比看起来是2:1,但是如同前文所言,ALaw仅仅使用了13bit的数据,uLaw使用了14bit的数据,都是取的数据的MSB开始的部分.所以压缩比其实没有这么大的.
现在开始用程序来对这个原始文件分别进行ALaw/uLaw的编码/解码.为了更好的兼容性,直接使用python的标准库函数audioop,ALaw/uLaw的代码分别如下:
【实验】2:Python制作ALaw和uLaw数据
ALaw测试代码:
# ALaw Encode Test using the audioop package
# Author: zhanzr21 @ 21ic BBS
#
import math
import sys
import audioop
DEFAULT_INPUT = 'test_8k16bitmono.bin'
DEFAULT_OUTPUT = 'test_8k16bitmono.alaw'
DEFAULT_BACK = 'test_8k16bitmono.aback'
raw_name = ''
alaw_name = ''
back_name = ''
def alaw_encode(in_name, out_name):
fin = open(in_name, mode='rb')
fout = open(out_name, mode='wb')
raw_data = fin.read()
fin.close()
test_ba = audioop.lin2alaw(raw_data, 2)
fout.write(test_ba)
fout.close()
return
def alaw_decode(in_name, out_name):
fin = open(in_name, mode='rb')
fout = open(out_name, mode='wb')
raw_data = fin.read()
fin.close()
test_ba = audioop.alaw2lin(raw_data, 2)
fout.write(test_ba)
fout.close()
return
if __name__ == "__main__":
if(2 <= len(sys.argv)):
raw_name = sys.argv[1]
else:
raw_name = DEFAULT_INPUT
if(3 <= len(sys.argv)):
alaw_name = sys.argv[2]
else:
alaw_name = DEFAULT_OUTPUT
if(4 <= len(sys.argv)):
back_name = sys.argv[3]
else:
back_name = DEFAULT_BACK
alaw_encode(raw_name, alaw_name)
#for verification
alaw_decode(alaw_name, back_name)
#for compare with Audacity
alaw_decode('test_8k16bitmono_ref.alaw', 'test_8k16bitmono_ref.aback')
uLaw测试代码:
# uLaw Encode Test using the audioop package
# Author: zhanzr21 @ 21ic BBS
#
import math
import sys
import audioop
DEFAULT_INPUT = 'test_8k16bitmono.bin'
DEFAULT_OUTPUT = 'test_8k16bitmono.ulaw'
DEFAULT_BACK = 'test_8k16bitmono.uback'
raw_name = ''
ulaw_name = ''
back_name = ''
def ulaw_encode(in_name, out_name):
fin = open(in_name, mode='rb')
fout = open(out_name, mode='wb')
raw_data = fin.read()
fin.close()
test_ba = audioop.lin2ulaw(raw_data, 2)
fout.write(test_ba)
fout.close()
return
def ulaw_decode(in_name, out_name):
fin = open(in_name, mode='rb')
fout = open(out_name, mode='wb')
raw_data = fin.read()
fin.close()
test_ba = audioop.ulaw2lin(raw_data, 2)
fout.write(test_ba)
fout.close()
return
if __name__ == "__main__":
if(2 <= len(sys.argv)):
raw_name = sys.argv[1]
else:
raw_name = DEFAULT_INPUT
if(3 <= len(sys.argv)):
ulaw_name = sys.argv[2]
else:
ulaw_name = DEFAULT_OUTPUT
if(4 <= len(sys.argv)):
back_name = sys.argv[3]
else:
back_name = DEFAULT_BACK
ulaw_encode(raw_name, ulaw_name)
#for verification
ulaw_decode(ulaw_name, back_name)
#for compare with Audacity
ulaw_decode('test_8k16bitmono_ref.ulaw', 'test_8k16bitmono_ref.uback')
【实验】3:SNR计算
SNR计算代码:
#SNR Test for 16bit PCM data
#Author: zhanzr21 @ 21ic BBS
import math
import sys
import audioop
EFAULT_INPUT_A = 'test_8k16bitmono.aback'
EFAULT_INPUT_U = 'test_8k16bitmono.Uback'
DEFAULT_REF = 'test_8k16bitmono.bin'
inA_name = ''
inU_name = ''
ref_name = ''
def SNR_S16(input16, ref16):
EnergySignal = 0.0
EnergyError = 0.0
SNR = 0.0
temp = 0
for i in range(len(input16)//2):
#input value
u16_sample = input16[i*2] + input16[1 + i*2] * 256
#unsigned to signed
if(u16_sample>32767):
test_sample = u16_sample - 65536
else:
test_sample = u16_sample
#normalization
test = test_sample / 32768
#Ref value
u16_sample = ref16[i*2] + ref16[1 + i*2] * 256
#unsigned to signed
if(u16_sample>32767):
test_sample = u16_sample - 65536
else:
test_sample = u16_sample
#normalization
ref = test_sample / 32768
EnergySignal = EnergySignal + ref * ref
EnergyError = EnergyError + (ref - test) * (ref - test)
try:
SNR = 10 * math.log10 (EnergySignal / EnergyError);
except ZeroDivisi:
SNR = math.inf
return (SNR)
def SNR_S16_FILE(inF, refF):
fin = open(inF, mode='rb')
ba_in = fin.read()
fin.close()
fref = open(refF, mode='rb')
ba_ref = fref.read()
fref.close()
if(len(ba_in) != len(ba_ref)):
print("Size Not Equal %s,%s" % inF, refF)
return 0
else:
return SNR_S16(ba_in, ba_ref)
if __name__ == "__main__":
if(2 <= len(sys.argv)):
inA_name = sys.argv[1]
else:
inA_name = EFAULT_INPUT_A
if(3 <= len(sys.argv)):
inU_name = sys.argv[2]
else:
inU_name = EFAULT_INPUT_U
if(4 <= len(sys.argv)):
ref_name = sys.argv[3]
else:
ref_name = DEFAULT_REF
print('Ref SNR:%f' % SNR_S16_FILE(ref_name, ref_name))
print('alaw SNR:%f' % SNR_S16_FILE(inA_name, ref_name))
print('ulaw SNR:%f' % SNR_S16_FILE(inU_name, ref_name))
#for comparign with Audacity result
print('Audicatiy alaw SNR:%f' % SNR_S16_FILE('test_8k16bitmono_ref.aback', ref_name))
print('Audicatiy ulaw SNR:%f' % SNR_S16_FILE('test_8k16bitmono_ref.uback', ref_name))
分别运行以上三个脚本,就能得到ALaw编码,uLaw编码文件,以及同library解码的文件,另外为了参考,把Audacity的编码文件也使用audioop进行了解码.
SNR计算的结果:
Ref SNR:inf
alaw SNR:37.544108
ulaw SNR:37.150272
Audicatiy alaw SNR:37.523572
Audicatiy ulaw SNR:37.166987
可以看出audioop编码的SNR要比Audacity的效果有小小差别,也有可能是两者对原始数据的量化取舍方法不同导致.另外ALaw在我们这个例子中取得SNR稍稍好于uLaw的结果.这是因为这段音频的本身特点决定的.
在板子上播放G711数据
【训练】:板子播放
(以GD32F105开发板为例)
C语言解码G711,已经有非常多的例子,优化也很成熟了.这里参考已有的SpanDSP工程中的代码给出解码代码片段.其余代码因为跟之前的文章重复较多请参考共享文件夹中的工程.总体来说,把原理搞懂之后,G711是非常简单的算法,一个sample对应一个sample.可以说G711是常用的算法中,最简单的音频编解码算法.
C语言解码ALaw/uLaw代码:
#define ULAW_BIAS 0x84 /* Bias for linear code. */
#define ALAW_AMI_MASK 0x55
static __inline int16_t alaw_to_linear(uint8_t alaw) {
int i;
int seg;
alaw ^= ALAW_AMI_MASK;
i = ((alaw & 0x0F) << 4);
seg = (((int) alaw & 0x70) >> 4);
if (seg)
i = (i + 0x108) << (seg - 1);
else
i += 8;
return (int16_t)((alaw & 0x80) ? i : -i);
}
/*! brief Decode an u-law sample to a linear value.
param ulaw The u-law sample to decode.
return The linear value.
*/
static __inline int16_t ulaw_to_linear(uint8_t ulaw) {
int t;
/* Complement to obtain normal u-law value. */
ulaw = ~ulaw;
/*
* Extract and bias the quantization bits. Then
* shift up by the segment number and subtract out the bias.
*/
t = (((ulaw & 0x0F) << 3) + ULAW_BIAS) << (((int) ulaw & 0x70) >> 4);
return (int16_t)((ulaw & 0x80) ? (ULAW_BIAS - t) : (t - ULAW_BIAS));
}
相比较而言,ITU官方给出的代码使用浮点计算的思路,代码显得臃肿一点.
ITU的ALaw解码参考代码:
void alaw_expand(lseg, logbuf, linbuf)
long lseg;
short *linbuf;
short *logbuf;
{
short ix, mant, iexp;
long n;
for (n = 0; n < lseg; n++)
{
ix = logbuf[n] ^ (0x0055); /* re-toggle toggled bits */
ix &= (0x007F); /* remove sign bit */
iexp = ix >> 4; /* extract exponent */
mant = ix & (0x000F); /* now get mantissa */
if (iexp > 0)
mant = mant + 16; /* add leading '1', if exponent > 0 */
mant = (mant << 4) + (0x0008); /* now mantissa left justified and */
/* 1/2 quantization step added */
if (iexp > 1) /* now left shift according exponent */
mant = mant << (iexp - 1);
linbuf[n] = logbuf[n] > 127 /* invert, if negative sample */
? mant
: -mant;
}
}
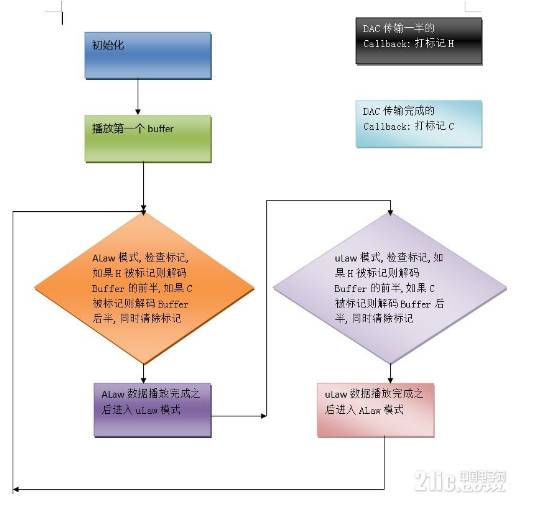
程序流程:
图 软件流程图
F105播放ALaw/uLaw的图片:
图 F105播放G711音频
关于GD32F105开发板:
此开发板是作者专门为嵌入式音频处理学习所制作的,或许不久之后即可开开放领取,请大家期待!
G711的扩展
截止本文写作时,G711标准有两个扩展:G711.0与G711.1.G711.0也称作G711 LLC,也就是无损压缩扩展.因为经过了进一步的压缩,带宽又可降低一半左右.G711.1则是对原G711的64Kbps的扩展.可以选择80,96Kbps的带宽来提高传输的质量.因为目前带宽资源的发展较快,可以预见G711.1的采用会有比较快的进展.因为篇幅原因,本文不对这两个扩展作展开讨论,感兴趣的同学可以参考ITU官方文档以了解更多细节.
总结
G711是最简单的音频编解码算法,但是应用非常广泛.从数字电话到网络语音会议,都能见到他的影子.原因在于其标准化的历史悠久,另外因为其算法简单,能在几乎所有处理器上轻易实现.了解了G711,可以说对数字电话入了门,也算是怀了一把旧.美中不足的是,如果不算上还没有广泛应用的G711.0的压缩扩展,G711的压缩比还是比较寒酸的.压缩比更加高的算法将在后面的章节陆续登场,敬请期待!