BitMap C++实现
1. Bit Map算法简介
来自于《编程珠玑》。所谓的Bit-map就是用一个bit位来标记某个元素对应的Value, 而Key即是该元素。由于采用了Bit为单位来存储数据,因此在存储空间方面,可以大大节省。
2、 Bit Map的基本思想
我们先来看一个具体的例子,假设我们要对0-7内的5个元素(4,7,2,5,3)排序(这里假设这些元素没有重复)。那么我们就可以采用Bit-map的方法来达到排序的目的。要表示8个数,我们就只需要8个Bit(1Bytes),首先我们开辟1Byte的空间,将这些空间的所有Bit位都置为0,如下图:
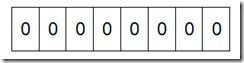
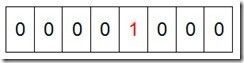
然后遍历这5个元素,首先第一个元素是4,那么就把4对应的位置为1(可以这样操作 p+(i/8)|(0x01<<(i%8)) 当然了这里的操作涉及到Big-ending和Little-ending的情况,这里默认为Big-ending),因为是从零开始的,所以要把第五位置为一(如下图):
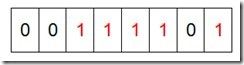
然后再处理第二个元素7,将第八位置为1,,接着再处理第三个元素,一直到最后处理完所有的元素,将相应的位置为1,这时候的内存的Bit位的状态如下:
然后我们现在遍历一遍Bit区域,将该位是一的位的编号输出(2,3,4,5,7),这样就达到了排序的目的。
优点:
1.运算效率高,不许进行比较和移位;
2.占用内存少,比如N=10000000;只需占用内存为N/8=1250000Byte=1.25M。
缺点:
所有的数据不能重复。即不可对重复的数据进行排序和查找。
算法思想比较简单,但关键是如何确定十进制的数映射到二进制bit位的map图。
3、 Map映射表
假设需要排序或者查找的总数N=10000000,那么我们需要申请内存空间的大小为int a[1 + N/32],其中:a[0]在内存中占32为可以对应十进制数0-31,依次类推:bitmap表为:
a[0]--------->0-31
a[1]--------->32-63
a[2]--------->64-95
a[3]--------->96-127
..........
那么十进制数如何转换为对应的bit位,下面介绍用位移将十进制数转换为对应的bit位。
3、 位移转换
申请一个int一维数组,那么可以当作为列为32位的二维数组,
| 32位 |
int a[0] |0000000000000000000000000000000000000|
int a[1] |0000000000000000000000000000000000000|
………………
int a[N] |0000000000000000000000000000000000000|
例如十进制0,对应在a[0]所占的bit为中的第一位: 00000000000000000000000000000001
0-31:对应在a[0]中
i =0 00000000000000000000000000000000
temp=0 00000000000000000000000000000000
answer=1 00000000000000000000000000000001
i =1 00000000000000000000000000000001
temp=1 00000000000000000000000000000001
answer=2 00000000000000000000000000000010
i =2 00000000000000000000000000000010
temp=2 00000000000000000000000000000010
answer=4 00000000000000000000000000000100
i =30 00000000000000000000000000011110
temp=30 00000000000000000000000000011110
answer=1073741824 01000000000000000000000000000000
i =31 00000000000000000000000000011111
temp=31 00000000000000000000000000011111
answer=-2147483648 10000000000000000000000000000000
32-63:对应在a[1]中
i =32 00000000000000000000000000100000
temp=0 00000000000000000000000000000000
answer=1 00000000000000000000000000000001
i =33 00000000000000000000000000100001
temp=1 00000000000000000000000000000001
answer=2 00000000000000000000000000000010
i =34 00000000000000000000000000100010
temp=2 00000000000000000000000000000010
answer=4 00000000000000000000000000000100
i =61 00000000000000000000000000111101
temp=29 00000000000000000000000000011101
answer=536870912 00100000000000000000000000000000
i =62 00000000000000000000000000111110
temp=30 00000000000000000000000000011110
answer=1073741824 01000000000000000000000000000000
i =63 00000000000000000000000000111111
temp=31 00000000000000000000000000011111
answer=-2147483648 10000000000000000000000000000000
浅析上面的对应表,分三步:
1.求十进制0-N对应在数组a中的下标:
十进制0-31,对应在a[0]中,先由十进制数n转换为与32的余可转化为对应在数组a中的下标。比如n=24,那么 n/32=0,则24对应在数组a中的下标为0。又比如n=60,那么n/32=1,则60对应在数组a中的下标为1,同理可以计算0-N在数组a中的下标。
2.求0-N对应0-31中的数:
十进制0-31就对应0-31,而32-63则对应也是0-31,即给定一个数n可以通过模32求得对应0-31中的数。
3.利用移位0-31使得对应32bit位为1.
找到对应0-31的数为M, 左移M位:即2^M. 然后置1.
由此我们计算10000000个bit占用的空间:
1byte = 8bit
1kb = 1024byte
1mb = 1024kb
占用的空间为:10000000/8/1024/1024mb。
大概为1mb多一些。
3、 扩展
Bloom filter可以看做是对bit-map的扩展
4、 Bit-Map的应用
1)可进行数据的快速查找,判重,删除,一般来说数据范围是int的10倍以下。
2)去重数据而达到压缩数据
5、 Bit-Map的具体实现
|
1
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 |
#include #include #include using namespace std; class BitMap { public: //功能:初始化bitmap //参数: size:bitmap的大小,即bit位的个数 // start:起始值 //返回值:0表示失败,1表示成功 BitMap( int size, int start): g_bitmap( NULL), g_size(size / 8 + 1) { g_bitmap = new char[g_size](); if(g_bitmap == NULL) { throw "new[] error"; } // memset(g_bitmap, 0x0, g_size); } ~BitMap() { delete [] g_bitmap; } //功能:将值index的对应位设为1 //index:要设的值 //返回值:0表示失败,1表示成功 int bitmap_set( int index) { int quo = (index) / 8 ; //确定所在的字节 int remainder = (index) % 8; //字节内的偏移 unsigned char x = (0x1 << remainder); if( quo > g_size) return 0; g_bitmap[quo] |= x; //所在字节内的特定位置为1 return 1; } //功能:取bitmap第i位的值 //i:待取位 //返回值:-1表示失败,否则返回对应位的值 int bitmap_get( int i) { int quo = (i) / 8 ; int remainder = (i) % 8; unsigned char x = (0x1 << remainder); unsigned char res; if( quo > g_size) return - 1; res = g_bitmap[quo] & x; return res > 0 ? 1 : 0; } //功能:返回index位对应的值 int bitmap_data( int index) { return (index); } private: char *g_bitmap; int g_size; }; class TwoBitMap { public: //功能:初始化bitmap //参数: size:bitmap的大小,即bit位的个数 // start:起始值 //返回值:0表示失败,1表示成功 TwoBitMap( int size): g_bitmap( NULL), g_size(size / 4 + 1) { g_bitmap = new char[g_size](); if(g_bitmap == NULL) { throw "new[] error"; } // memset(g_bitmap, 0x0, g_size); } ~TwoBitMap() { delete [] g_bitmap; } //x表示一个整数,num表示bitmap中已经拥有x的个数 //由于我们只能用2个bit来存储x的个数,所以num的个数最多为3 int set( int x, int num) { if(x > (g_size - 1) * 4) return - 1; int m = x >> 2; int n = x & 3; //将x对于为值上的个数值先清零,但是有要保证其他位置上的数不变 g_bitmap[m] &= ~((0x3 << ( 2 * n)) & 0xFF); //重新对x的个数赋值 g_bitmap[m] |= ((num & 3) << ( 2 * n) & 0xFF); return 0; } /* 对X位进行置零处理 */ int clear( int x) { if(x > (g_size - 1) * 4) return - 1; int m = x >> 2; int n = x & 3; g_bitmap[m] &= ~((0x3 << ( 2 * n)) & 0xFF); return 0; } /* 获取X为的数字 */ int get( int x) { if(x > (g_size - 1) * 4) return - 1; int m = x >> 2; int n = x & 3; return (g_bitmap[m] & (0x3 << ( 2 * n))) >> ( 2 * n); return 0; } /* 对X位进行加1处理 */ int add( int x) { if(x > (g_size - 1) * 4) return - 1; int num = get(x); set(x, num + 1); return 0; } private: char *g_bitmap; int g_size; }; int main() { int a[] = { 5, 8, 7, 6, 3, 1, 10, 78, 56, 34, 23, 12, 43, 54, 65, 76, 87, 98, 89, 100}; int i; TwoBitMap s( 100); for(i = 0; i < 20; i++) { s.set(a[i], 1); } for(i = 0; i <= 100; i++) { int m = s.get(i); cout << m << ","; } cout << endl; return 0; } |