使用Tensorflow处理Mnist手写数据集
使用Tensorflow处理Mnist手写数据集
Mnist手写数据集是一个入门级的计算机视觉数据集,何谓入门呢?可以这样说,MNIST 问题就相当于图像处理的 Hello World 程序。下面我将使用Tensorflow搭建CNN卷积神经网络来处理MNIST数据集,来一步步的熟悉Tensorflow和CNN。
MNIST数据集介绍
MNIST数据集是一个手写体数据集,简单说就是一堆这样东西:
MNIST的官网地址是MNIST; 通过阅读官网我们可以知道,这个数据集由四部分组成,分别是
;

当然下载下来的数据集被分成两部分:60000行的训练数据集(mnist.train)和10000行的测试数据集(mnist.test)。这样的切分很重要,在机器学习模型设计时必须有一个单独的测试数据集不用于训练而是用来评估这个模型的性能,从而更加容易把设计的模型推广到其他数据集上(泛化)。
我们可以看出这个其实并不是普通的文本文件或是图片文件,而是一个压缩文件,下载并解压出来,里面看到的是二进制文件。
一张图片包含28像素X28像素。我们可以用一个数字数组来表示这张图片:
我们把这个数组展开成一个向量,长度是 28x28 = 784。如何展开这个数组(数字间的顺序)不重要,只要保持各个图片采用相同的方式展开。从这个角度来看,MNIST数据集的图片就是在784维向量空间里面的点。
因此,在MNIST训练数据集中,mnist.train.images 是一个形状为 [60000, 784] 的张量,第一个维度数字用来索引图片,第二个维度数字用来索引每张图片中的像素点。在此张量里的每一个元素,都表示某张图片里的某个像素的强度值,值介于0和1之间。
相对应的MNIST数据集的标签是介于0到9的数字,用来描述给定图片里表示的数字。比如,标签0将表示成([1,0,0,0,0,0,0,0,0,0,0])。因此, mnist.train.labels 是一个 [60000, 10] 的数字矩阵。
输入集
得到数据集可以直接使用下面代码,程序会直接下载代码到MNIST_data文件夹中,或者在MNIST数据集的官网Yann LeCun’s website下载。
import input_data
mnist = input_data.read_data_sets("MNIST_data/", one_hot=True)
使用卷积神经网络处理数据集
卷积神经网络介绍
神经网络由大量的神经元相互连接而成。每个神经元接受线性组合的输入后,最开始只是简单的线性加权,后来给每个神经元加上了非线性的激活函数,从而进行非线性变换后输出。每两个神经元之间的连接代表加权值,称之为权重(weight)。不同的权重和激活函数,则会导致神经网络不同的输出。
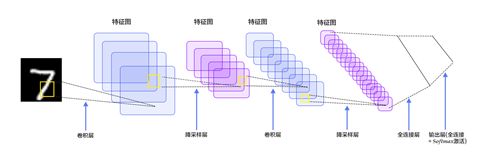
给定一个未知数字,让神经网络识别是什么数字。此时的神经网络的输入由一组被输入图像的像素所激活的输入神经元所定义。在通过非线性激活函数进行非线性变换后,神经元被激活然后被传递到其他神经元。重复这一过程,直到最后一个输出神经元被激活。从而识别当前数字是什么字,如下图结构所示:
下面推荐一篇博文,我认为介绍神经网络介绍的很详细:通俗理解卷积神经网络
定义计算图
使用 TensorFlow, 你必须明白 TensorFlow:
- 使用图 (graph) 来表示计算任务.
- 在被称之为
会话 (Session)的上下文 (context) 中执行图. - 使用 tensor 表示数据.
- 通过
变量 (Variable)维护状态. - 使用 feed 和 fetch 可以为任意的操作(arbitrary operation) 赋值或者从其中获取数据.
下面我们将定义一个多层卷积网络
权重初始化
为了创建这个模型,我们需要创建大量的权重和偏置项。这个模型中的权重在初始化时应该加入少量的噪声来打破对称性以及避免0梯度。由于我们使用的是ReLU神经元,因此比较好的做法是用一个较小的正数来初始化偏置项,以避免神经元节点输出恒为0的问题(dead neurons)。为了不在建立模型的时候反复做初始化操作,我们定义两个函数用于初始化。
# 定义一个函数,用于初始化所有的权值 W
def weight_variable(shape):
initial = tf.truncated_normal(shape, stddev=0.1)
return tf.Variable(initial)
# 定义一个函数,用于初始化所有的偏置项 b
def bias_variabls(shape):
initial = tf.constant(0.1, shape=shape)
return tf.Variable(initial)
卷积和池化
TensorFlow在卷积和池化上有很强的灵活性。我们怎么处理边界?步长应该设多大?在这个实例里,我们会一直使用vanilla版本。我们的卷积使用1步长(stride size),0边距(padding size)的模板,保证输出和输入是同一个大小。我们的池化用简单传统的2x2大小的模板做max pooling。为了代码更简洁,我们把这部分抽象成一个函数。
# 定义一个函数,用于构建卷积层,我们的卷积使用1步长(stride size),0边距(padding size)的模板,保证输出和输入是同一个大小。
def conv2d(x, W):
return tf.nn.conv2d(x, W, [1, 1, 1, 1], padding='SAME')
# 定义一个函数,用于构建池化层,我们的池化用简单传统的2x2大小的模板做max pooling。
def max_pool_2x2(x):
return tf.nn.max_pool(x, ksize=[1, 2, 2, 1], strides=[1, 2, 2, 1], padding='SAME')
第一层卷积
现在我们可以开始实现第一层了。它由一个卷积接一个max pooling完成。卷积在每个5x5的patch中算出32个特征。卷积的权重张量形状是[5, 5, 1, 32],前两个维度是patch的大小,接着是输入的通道数目,最后是输出的通道数目。 而对于每一个输出通道都有一个对应的偏置量。
# 构建网络
x_image = tf.reshape(x, [-1, 28, 28, 1]) # -1表示任意数量的样本数,大小为28x28深度为一的张量(变成一个4d向量,其第2、第3维对应图片的宽、高,最后一维代表图片的颜色通道数(
# 因为是灰度图所以这里的通道数为1,如果是rgb彩色图,则为3))
W_conv1 = weight_variable([5, 5, 1, 32]) # 将一个灰度图像映射到32个特征图,卷积核是 5*5*1 的,一共 32 个卷积核(
# 前两个维度是patch的大小,接着是输入的通道数目,最后是输出的通道数目。 而对于每一个输出通道都有一个对应的偏置量。)
b_conv1 = bias_variabls([32])
h_conv1 = tf.nn.relu(conv2d(x_image, W_conv1) + b_conv1) # 第一个卷积层
h_pool1 = max_pool_2x2(h_conv1) # 第一个池化层
第二层卷积
为了构建一个更深的网络,我们会把几个类似的层堆叠起来。第二层中,每个5x5的patch会得到64个特征。
W_conv2 = weight_variable([5, 5, 32, 64])
b_conv2 = bias_variabls([64])
h_conv2 = tf.nn.relu(conv2d(h_pool1, W_conv2) + b_conv2) # 第二个卷积层
h_pool2 = max_pool_2x2(h_conv2) # 第二个池化层
连接层
现在,图片尺寸减小到7x7,我们加入一个有1024个神经元的全连接层,用于处理整个图片。我们把池化层输出的张量reshape成一些向量,乘上权重矩阵,加上偏置,然后对其使用ReLU。
# full connection,图片尺寸减小到7x7,我们加入一个有1024个神经元的全连接层,用于处理整个图片。我们把池化层输出的张量reshape成一些向量,乘上权重矩阵,加上偏置,然后对其使用ReLU。
W_fc1 = weight_variable([7 * 7 * 64, 1024])
b_fc1 = bias_variabls([1024])
h_pool2_flat = tf.reshape(h_pool2, [-1, 7*7*64]) # reshape成向量
h_fc1 = tf.nn.relu(tf.matmul(h_pool2_flat, W_fc1) + b_fc1) # 第一个全连接层
Dropout
为了减少过拟合,我们在输出层之前加入dropout。我们用一个placeholder来代表一个神经元的输出在dropout中保持不变的概率。这样我们可以在训练过程中启用dropout,在测试过程中关闭dropout。 TensorFlow的tf.nn.dropout操作除了可以屏蔽神经元的输出外,还会自动处理神经元输出值的scale。所以用dropout的时候可以不用考虑scale。
h_fc1_drop = tf.nn.dropout(h_fc1, keep_prob) # dropout层(为了减少过拟合,我们在输出层之前加入dropout)
输出层
最后,我们添加一个softmax层,就像前面的单层softmax regression一样。
W_fc2 = weight_variable([1024, 10])
b_fc2 = bias_variabls([10])
y = tf.nn.softmax(tf.matmul(h_fc1_drop, W_fc2) + b_fc2) # softmax层
训练和评估模型
这个模型的效果如何呢?
为了进行训练和评估,我们使用与之前简单的单层SoftMax神经网络模型几乎相同的一套代码,只是我们会用更加复杂的ADAM优化器来做梯度最速下降,在feed_dict中加入额外的参数keep_prob来控制dropout比例。然后每100次迭代输出一次日志。
# train
y_ = tf.placeholder(tf.float32, [None, 10], name='y')
cross_entropy = -tf.reduce_sum(y_ * tf.log(y)) # 为训练过程指定最小化误差用的损失函数,我们的损失函数是目标类别和预测类别之间的交叉熵
train_step = tf.train.AdamOptimizer(1e-4).minimize(cross_entropy) # 梯度下降法,即学习率为1e-4的速度最小化损失函数 cross_entropy,
# 每次参数的变化值为1e-4
correct_prediction = tf.equal(tf.argmax(y, 1), tf.argmax(y_, 1))
accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32)) # 精确度计算
saver = tf.train.Saver(variables)
with tf.Session() as sess:
merged_summary_op = tf.summary.merge_all()
summay_writer = tf.summary.FileWriter('mnist_log/1', sess.graph)
summay_writer.add_graph(sess.graph)
sess.run(tf.global_variables_initializer())
# for i in range(20000):
for i in range(1000):
batch = data.train.next_batch(50)
if i % 100 == 0: # 训练100次,验证一次
train_accuracy = accuracy.eval(feed_dict={x: batch[0], y_: batch[1], keep_prob: 1.0})
print("step %d, training accuracy %g" % (i, train_accuracy))
sess.run(train_step, feed_dict={x: batch[0], y_: batch[1], keep_prob: 0.5})
print(sess.run(accuracy, feed_dict={x: data.test.images, y_: data.test.labels, keep_prob: 1.0}))
path = saver.save(
sess, os.path.join(os.path.dirname(__file__), 'data', 'convalutional.ckpt'),
write_meta_graph=False, write_state=False)
print("path:", path)
我们这里简单的训练的一千次,并且每隔100次打印一下正确率,可以得到如下输出结果:
step 0, training accuracy 0.04
step 100, training accuracy 0.82
step 200, training accuracy 0.92
step 300, training accuracy 0.98
step 400, training accuracy 0.94
step 500, training accuracy 0.94
step 600, training accuracy 0.98
step 700, training accuracy 0.98…
可以看到随着训练次数的提升,正确率不断提高。
图像化显示
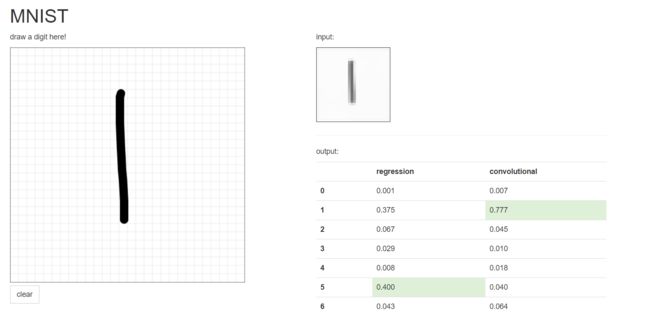
当然我们可以用一个前端图像化手写界面来形象的体现手写数字识别。
界面是使用的如下地址:
https://github.com/sugyan/tensorflow-mnist