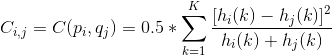图像形状特征(八)--SC形状上下文
形状上下文特征是一种很流行的形状描述子,多用于形状匹配,目标识别,它采用一种基于形状轮廓的特征描述方法,其在对数极坐标系下利用直方图描述形状特征能够很好地反映轮廓上采样点的分布情况。
形状上下文的基本原理如下:
Step1:对于给定的一个形状,通过边缘检测算子(如:canny算子)获取轮廓边缘 ,对轮廓边缘采样得到一组离散的点集P={p1,p2,p3,..pn},如图1中的字母A。
Step2:计算形状上下文。以其中任意一点pi为参考点,在pi为圆心、R为半径的局域内按对数距离间隔建立N个同心圆。将此区域沿圆周方向M等分,形成如图1所示的靶状模板。点pi到其它各点的向量相对位置简化为模板上各扇区内的点分布数。这些点的统计分布直方图hi(k),称为点pi的形状上下文,其计算公式为:
其中,k={1,2,……,K},K=M*N;
图1
图2
采用对数距离分割可以使形状上下文描述子对邻近的采样点比远离点更敏感,能强化局部特征。轮廓不同点处的形状上下文是不同的,但相似轮廓的对应点处趋于有相似的形状上下文,如图2。
对于整个点集P ,分别以其n个点 p1,p2,p3,..pn作参考点,依次计算与剩下的n-1个点构成的形状直方图,最终得到 n个形状直方图。以n*(n-1)大小的矩阵存储。这样,对于任一目标,可用n*(n-1)大小的矩阵表示其形状信息,n*(n-1)大小的矩阵就是点集P的形状上下文,它描述了整个轮廓形状的特征。采样点越多,形状表达也越精细,计算量也会成倍加大。
利用步骤1,2得到每个目标的形状上下文后,接下来需要计算这两个目标的形状上下文的相似度,从而得到相似与否的结论。形状上下文之间的相似度计算方法叙述如下:
Step3:计算代价矩阵cost
计算一个目标的形状直方图与另一目标的形状直方图之间的匹配代价,代价函数如下:
其中,hi(k)为目标P的点pi的形状直方图;hj(k)为目标Q的点qi的形状直方图。
按照公式,即可得到两个目标之间的代价矩阵C,大小为n*n。
Step4:
然后,基于计算得到的代价矩阵C,进行点的匹配操作,使公式(2)获得最小值。
![]() (2)
(2)
经分析,上述点的匹配问题即为典型的双向图的匹配问题。利用匈牙利算法,该问题得到解决。
至此,该方法以一个非矢量的数值表示两个目标的相似度。由于是基于代价矩阵进行计算。所以结果越大表示越不相似,结果越小表示越相似。
优点:
充分利用上下文信息,在非刚性物体匹配中,具有很好的鲁棒性。
主要缺点:
1、标准的形状上下文不能很好地解决物体类内部之间的变形,后期改进的基于内部距离的形状上下文改善了一点;
2、对于有背景、噪声点过多的情况,匹配效果很不好。
参考:
http://blog.csdn.net/aivin24/article/details/8846293?reload
http://blog.csdn.net/u012507022/article/details/52437149
《shapematch-Belongie-Pami-ByContext》