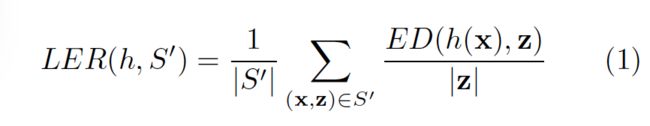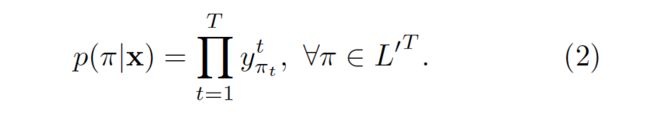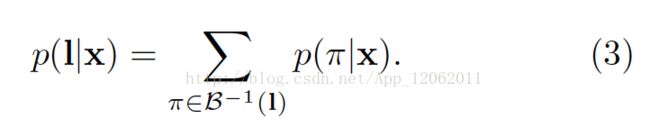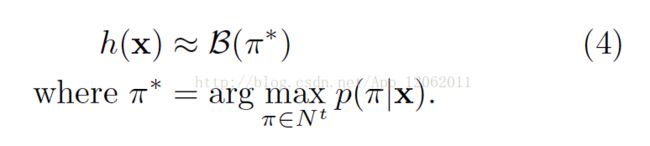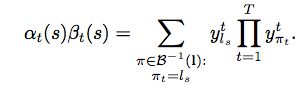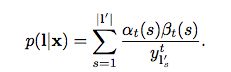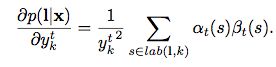系统学习深度学习(二十七)--CTC
论文:
Connectionist Temporal Classification: Labelling Unsegmented Sequence Data with Recurrent Neural Networks
Offline Arabic Handwriting Recognition with Multidimensional Neural Networks
Supervised Sequence Labelling with Recurrent Neural Networks
转自:http://blog.csdn.net/wqzghost/article/details/53044057
转自:http://www.jianshu.com/p/8406618e940f
转自:http://blog.csdn.net/xmdxcsj/article/details/51763886
理解这个之前,先推导一边HMM的三大问题,看这个相对来说比较简单。
许多真实世界中的序列学习任务,往往需要从噪声和未格式化的数据上,预测序列的label。例如,在语音识别中,一个声音信号被转换成words或者是sub-word单元。RNN是序列学习的一个强大的模型。但是,它要求预先分割(pre-segmented)的训练数据,通过后处理将模型输出转换为label序列,因此它的应用受到较大的限制。这篇文章提出了一个新的RNN训练方法,支持直接对未分割的序列上预测label。在TIMIT语料上,对比了HMM和HMM-RNN构成Baseline的效果。
一、介绍
label未分割的序列数据是一个普遍存在序列学习任务。尤其是在感知任务中,比如手写识别、语音识别、手势识别等,这些场景中噪声、真实输入数据流将被离散字符label表达,例如letters或者words。
目前,图模型例如HMM、CRF以及它们的变体,在序列label领域都是很有影响力的框架。虽然在很多问题上,这些方法都得到了很好的证明,但是他们仍然存在缺陷:
1)他们往往需要大量的任务相关的知识,例如涉及HMM的状态模型,或者选择CRF的输入特征。
2)他们往往依赖显示的模型假设,来保证推理inference容易处理,例如HMM的观察独立性假设。
3)对于标准的HMM,训练是生成式的,但是序列标注任务是判别式的。
在另外一方面,RNN模型在输入和输出的表达选择外,对数据不需要任何的先验知识prior knowledge。并且,通过判别式的方式训练,内部internal状态提供了强大且通用的机制来建模时间序列。此外,它对时间temporal和空间spatial上的噪声表现出鲁棒性。
但是,到目前为止,我们还不能将RNN直接应用到序列标注任务上。问题在于,标准的neural network的目标函数,是在训练序列的每个节点上,单独定义的。换句话说,RNN只能被用来处理一系列独立label分类任务。这意味着,训练数据必须是预先分割的,网络输出必须经过后处理来给出最终的label序列。
目前,序列label任务里最有效的使用RNN的方法,是与HMM结合在一起,构成所谓的Hybrid方法(Bourlard&Morgan;Bengio)。Hybrid系统使用HMM来建模数据中的long-range序列结构,使用neural nets来提供局部分类能力。HMM部分可以在训练过程中自动的分割segment序列,将网络分类转换成标签序列label sequence。但是,同样继承了HMM的缺点,hybrid系统没有充分利用RNN在序列模型上的潜力。
这篇文章提出了使用RNN标注序列数据的新方法,避免了对训练数据预先分隔以及输出后处理的要求,仅采用一个单独的网络架构建模对序列的全部方面进行建模。最基本的思路是将网络输出解释为,在给定输入下,所有可能对应的label序列上的一个概率分布。给定这个分布,目标函数可以是直接最大化正确label的概率。因为目标函数是可导的,网络可以通过标准的BP方法来训练(Werbos,1990)。
文章后续章节中,我们把未分割的数据序列的label任务,看成是时序分类temporal classification(Kadous,2002),把RNN的使用称为CTC(connectionist temporal classification)。与之相比,把输入序列上each time-step或者frame的独立label任务,称为framewise classification。
下一个章节给出了temporal分类的数据公式,定义了本文使用的误差度量方法。第3节描述了输出表示,允许使用RNN完成temporal 分类。第4节中解释了CTC网络如何训练。第5节比较了CTC和hybrid以及HMM系统。第6节讨论了CTC与其他temporal分类的一些关键区别,以及未来工作的规划。第7节是论文结尾。
二、时序分类Temporal classification
S代表训练集合,符合分布Dx×z。输入空间X=(Rm)*,代表m维具有真实值的向量,构成的序列的集合。目标空间Z=L*,代表标签Label的有限字符集合构成的序列的集合。一般来说,我们把L*中的元素看做是label序列或标签。S中的每个样本构成一个序列对(x,z)。目标序列Z=(z1,..zu)的长度至多与输入序列X=(x1,…,xt)等长,即U≤T。由于输入和目标序列一般都是不等长的,因此没有先验的方法可以对齐。
我们的目的是利用S来训练一个时序分类h:X->X,对未知的输入序列分类,最小化一些任务对应的误差量化指标。
1、标签错误率Label Error Rate
在这篇论文中,错误率的度量是比较关键的。考虑一个测试集合S`∈Dx×z,定义时序分类h的标签错误率LER(Label error rate)为:分类结果和目标的平均归一化编辑距离
ED(p,q)表示p和q两个序列的编辑距离。例如,将p变为q需要的最小的插入、替换和删除数。
LER是对于目标是减少转换错误率的任务(比如语音和手写识别)来说是最自然的度量方法。
三、CTC——Connectionist Temporal Classification
本节将描述使RNN支持CTC模型所需要的输出表示。关键步骤是将网络输出转换为一个在label序列上的条件概率分布。之后对于给定输入,网络通过选择最可能的label来完成分类。
1、从网络输出到Labellings
一个CTC网络具有softmax 输出层,该层比label集合L多出一个unit。对于|L|个units的触发被解释为在特定的时刻观察到对应的label的概率,对于多余的unit的出发被看做观察到空格或者no label的概率。总的来说,这些输出定义了将label序列对齐到输入序列的全部可能方法的概率。任何一个label序列的总概率,可以看做是它的不同对齐形式对应的全部概率累加。
更加正式的,对于一个给定的输入序列X,长度为T,定义一个RNN网络,m个输入,n个输出,权重向量w是一个连续映射Nw:(R^m)^T -> (R^n)^T。设Y=Nw(x)为网络的输出序列,y(k,t)表示输出单元k在t时刻被触发,被解释为在t时刻观察到label k的概率,这个观察定义了在字符集合L`=L∪{blank}的长度为T的序列的集合L`^T的概率分布。
其中 π=(π1,π1,...,πT) 表示的是选择的Label,π 也称为「路径」,可以发现路径的种数是指数级的L'^T
现在,我们把L`^T中的元素看做路径paths并且用π表示。公式(2)的假设是,给定网络的中间状态(internal state),在不同时刻的网络输出是条件独立的。这保证了输出层不存在到它自身或者网络的反馈链接。
在现实之中,多个路径会对应一个正确的序列,并且这个序列长度往往小于路径长度,那么序列最终的概率可以使用路径的概率之和表示.
下一步是定义一个多对一的映射β:L`^T -> L^≤T,其中后者是可能的label序列的集合。我们可以简单通过删除全部的blank和重复路径path中的label来实现,例如β(a-ab-)=β(-aa—abb)=aab
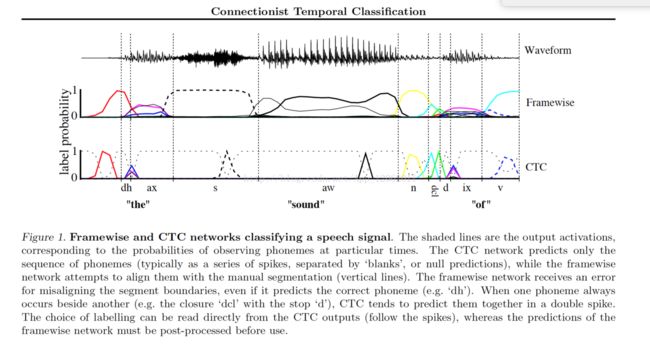
直觉地,这等价于输出一个新的label,从预测no label变为预测a label,或者从预测a label到预测另外一个label。参考Figure1
最终,我们用映射β来定义给定一个label序列l∈L^≤T的条件概率:与它对应的全部paths的概率和
2、设计分类器Constructing the Classifier
考虑上述公式,分类器的输出是对于输入序列最可能的label序列:
按照HMM的术语,发现label序列的任务被称为解码Decoding。很遗憾,对于我们的系统,找不到一个通用的、易处理的解码算法。但是下面的两个近似算法在实际工作中取得了不错的效果。
1)Best path decoding
假设:the most probable path π will correspond to the most probable labelling h
这种简化的方式是:找到路径中概率最大的,然后其对应的序列 I I 就是最优序列,这个方法被称为「Best path decoding」。
这个方法相当于是假设,最优序列的最优路径也是全局最优的(最优表示概率最大),形式化表示为
π*只是在每个时间片上最活跃输出的串联。但是,这个方法不保证能找到the most probable labelling。其实,实际就是DP的方式,与HMM解码类似。
2)Prefix search decoding
prefix search decoding是一种剪枝的算法,剪枝主要在两个方面,一是同路径不重复计算,二是不可能状态不再搜索,下图中第一层的Y不搜索就是因为同层的X和下层的Y概率都比他高。这是一种启发式搜索算法。
通过修改section 4.1里的forward-backward算法,我们可以高效的计算对于labelling prefixes的连续扩展(successive extensions)的概率。
只要给足够的时间,prefix search decoding 方法总能找到the most probable labelling。但是,随着输入数列长度的增加,需要扩展的最大的前缀prefix数量会指数性的增加。如果输出概率分布在mode周围足够的peak,这个方法会在合理的时间内收敛。在本文的实验中,需要一个启发式方法来保证这个方法可以应用。
观察到CTC网络的输出倾向于被blank分隔开的峰值spikes,我们根据以blank开始和结束,将输出序列分割成片段。通过选择边界点(观察到blank label的概率大于一定的阈值)来实现上面的分割。之后,我们为每个片段,独立的计算the most probable labelling,并且将它们串联在一起得到最后的分类结果。
在实际中,prefix search 方法与这个启发式方法配合的比较好,通常效果超过best path decoding。但是在一些情况下,它确实会失败,例如当同样的label在边界点两边出现时。
四、网络训练Training the Network
前期准备
- 输入 x ,长度为T
- 输出集合
A 表示正常的输出
A ′ =A⋃{blank} 表示输出全集
A ′T 表示输入x对应的输出元素集合 - 输出序列
π 表示输出路径
l 表示输出label序列
F 表示路径到label序列的映射关系 - 概率
y t k 表示时间t输出k的概率
p(π|x)=∏ t=1 T y t π t 表示基于输入x的输出π 路径的概率
p(l|x)=∑ π∈F −1 (l) p(π|x) 表示输出label序列的概率是多条路径的概率和。
前后向算法

考虑到计算p(l|x) 需要计算很多条路径的概率,随着输入长度呈指数化增加,可以引入类似于HMM的前后向算法来计算该概率值。
为了引入blank节点,在label首尾以及中间插入blank节点,如果label序列原来的长度为U,那么现在变为U’=2U+1。
前向
前向变量为α(t,u) ,表示t时刻在节点u的前向概率值,其中u∈[1,2U+1] .
初始化值如下:
α(1,1)=y 1 b
α(1,2)=y 1 l 1
α(1,u)=0,∀u>2
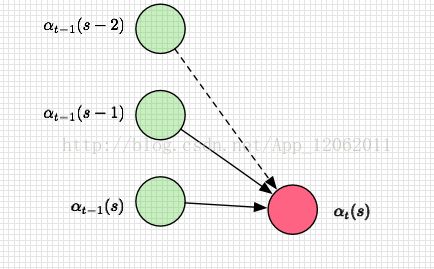
递推关系(也就是状态转移方程):
α(t,u)=y t l ′ u ∑ i=f(u) u α(t−1,i)
其中
f(u)={u−1u−2 if l ′ u =blank or l ′ u−2 =l ′ u otherwise
注:如果l表示{c,a,t},那么l’表示为{b,c,b,a,b,t,b},所以原来在l中的下标u为2,在l’中的下标u变为4。
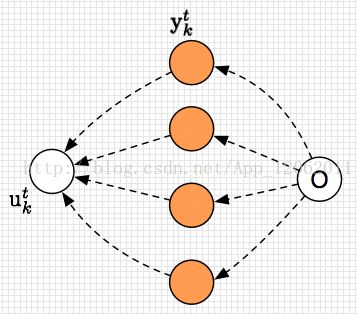
α(t,u)=0∀u 对应于上图中的右上角部分,因为时间的限制,有些节点不可能到达最后的终止节点。 初始化值: β(T,U ′ )=1 β(T,U ′ −1)=1 β(T,u)=0,∀u α(1,u)=0,∀u>2 β(t,u)=∑ i=u g(u) β(t+1,i)y t+1 l ′ i g(u)={u+1u+2 if l ′ u =blank or l ′ u+2 =l ′ u otherwise 概率计算在log计算,避免underflow,其中log加可以通过以下形式转化: ln(a+b)=lna+ln(1+e lnb−lna ) CTC的loss function使用最大似然: L(S)=∑ (x,z)∈S L(x,z) L(x,z)=−lnp(z|x) p(z|x)=∑ u=1 |z ′ | α(t,u)β(t,u) L(x,z)=−ln∑ u=1 |z ′ | α(t,u)β(t,u) 这里介绍一种快速计算(上文p(z|x)少除了一个ykt),如果保证t时刻生成 ls ,那么整个label生成的概率是多少?首先理解一下下面式子的物理意义: 用一个图形象表示一下,可以表示为: 这个计算过程,将 y t s yst 计算了两次,所以除以 y t s yst 表示的就是t时刻生成 l s ls 的约束下,整条label生成的概率: 这里就容易推导出来,表示整个样本生成的概率公式了,穷举所有可切割位置,将他们加和到一起即可: y t k 表示t时刻输出k的概率 ∂L(x,z)∂y t k =−1p(z|x) ∂p(z|x)∂y t k ∂p(z|x)∂y t k =∑ u∈B(z,k) ∂α(t,u)β(t,u)∂y t k α(t,u)β(t,u)=∑ π∈X(t,u) ∏ t=1 T y t π t ∂p(z|x)∂y t k =∑ u∈B(z,k) α(t,u)β(t,u)y t k ∂L(x,z)∂y t k =−1p(z|x)y t k ∑ u∈B(z,k) α(t,u)β(t,u) ∂L(x,z)∂a t k =y t k −1p(z|x) ∑ u∈B(z,k) α(t,u)β(t,u) 我们的目标是希望得到路径上面每一个点的梯度,损失函数是极大似然的前提下,如何将梯度简化的表示(求解)是需要考虑的问题。具体计算的时候,梯度需要沿着每一个时刻的每一个分类往后传,所以需要对y t k ykt 求偏导数, y t k ykt 的 k k 表示的是第k个分类,具体偏导为: 需要好好理解一下 s∈lab(l,k) s∈lab(l,k) ,表达的意思是所有 l s =k ls=k 的 s s 的集合,因为满足条件的地方都是潜在的 y t k ykt 的概率贡献方。 整个似然函数对softmax未归一化之前的变量求偏导数得到(下面有链接详细介绍这个推导过程): 梯度反向传播的过程如下图: https://github.com/baidu-research/warp-ctc/blob/master/README.zh_cn.md
根据上图,很容易理解前向的递推关系。f(u)条件表示在空格处,和相同label情况下,不能转移。另外一份图解:后向
递推关系:
其中取log
训练
loss function
根据前后向变量,可以求得:
|z ′ | 表示z对应的label长度的U’,α(t,u)β(t,u) 表示t时刻经过节点u的所有路径的概率和。bp训练
a t k 表示t时刻对应输出节点k在做softmax转换之前的值
只需要考虑t时刻经过k节点的路径即可
其中B(z,k) 表示节点为k的集合
考虑到
其中X(t,u) 表示所有在t时刻经过节点u的路径。
所以
可以到损失函数对y t k 偏导数
同时可以得到损失函数对于a t k 偏导数
关于Uk推导:https://www.zhihu.com/question/53399706