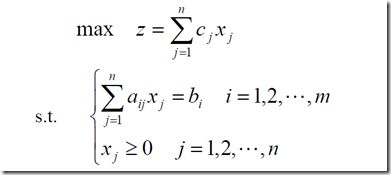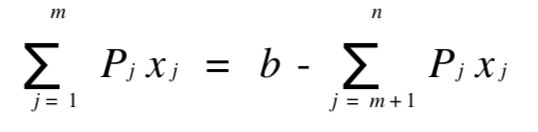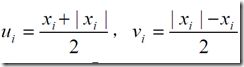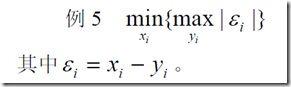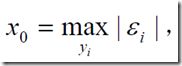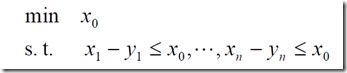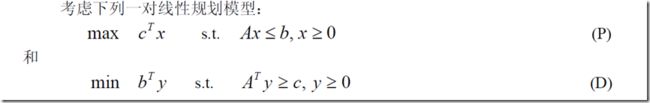运筹优化（二）--线性规划概念及应用模型

一、解决问题

     线性规划问题是在一组线性约束下，求线性目标函数的最大最小值的问题。

二、数学模型

1、一般数学模型

2、矩阵表示

其中c,x都是列向量，A，Aeq是一个合适的矩阵，b,beq是合适的列向量。然后lb和ub是下限和上限（但是请注意lb是一个变量的名字）。

注意：这里针对变量类型约束增加上下限的约束，其目的在于减少主要约束Ax=b中的行数，从而简化计算。本质上，跟标准的非负类型约束一致。

实际碰到各种线性规划问题的数学模型都应变换为标准型式后求解。

以下讨论如何变换为标准型的问题。

(1 ) 若要求目标函数实现最小化, 即 min z = CX。这时只需将目标函数最小化变换求目标函数最大化 , 即令z′= -z , 于是得到max z′= -CX。 这就同标准型的目标函数的形式一致了。

(2) 约束方程为不等式。这里有两种情况: 一种是约束方程为“≤”不等式, 则可在 “≤”不等式的左端加入非负松弛变量, 把原“≤”不等式变为等式; 另一种是约束方程为 “ ≥ ”不等式 , 则可在“ ≥ ”不等式的左端减去一个非负剩余变量 (也可称松弛变量）, 把不等式约束条件变为等式约束条件。

(3) 若存在取值无约束的变量xk ,可令xk = x′k - x′′k ,其中 x′k , x′′k ≥0。

线性规划问题的解的概念

在讨论线性规划问题的求解前, 先要了解线性规划问题的解的概念。我们针对线性规划的一般数学模型来说明：

1. 可行解

满足约束条件的解X=(x1 ,x2 ,⋯,xn)T ,称为线性规划问题的可行解 , 其中使目标函数达到最大值的可行解称为最优解。

2. 基

设 A是约束方程组的 m×n维系数矩阵,其秩为 m。B是矩阵 A中 m×m阶非奇异子矩阵( | B| ≠0) ,则称B是线性规划问题的一个基。这就是说, 矩阵B是由 m个线性独立的列向量组成。为不失一般性 , 可设：

称 Pj (j=1,2,⋯,m)为基向量,与基向量 Pj 相应的变量 xj (j=1,2,⋯,m)为基变量,否则称为非基变量 , 为了进一步讨论线性规划问题的 解, 下面研究约束方程组(1-5 ) 的 求 解 问题。假设该方程组系数矩阵 A 的秩为 m , 因 m < n, 故它有无穷多个解。假设前 m 个变 量的系数列向量是线性独立的。这时(1 -5)式可写成：

设 XB 是对应于这个基的基变量：XB =(x1,x2,⋯,xm)T ，

现若令上式的非基变量 xm + 1 = xm + 2 = ⋯ = xn = 0, 这时变量的个数等于线性方程的个数。用高斯消去法 , 求出一个解：

X=(x1 ,x2 ,⋯,xm ,0,⋯,0)T

该解的非零分量的数目不大于方程个数 m, 称 X 为基解。由此可见 , 有一个基 , 就可以求出一个基解。

3. 基可行解
同时满足非负条件的可行解和基解的解,称为基可行解。

4. 可行基

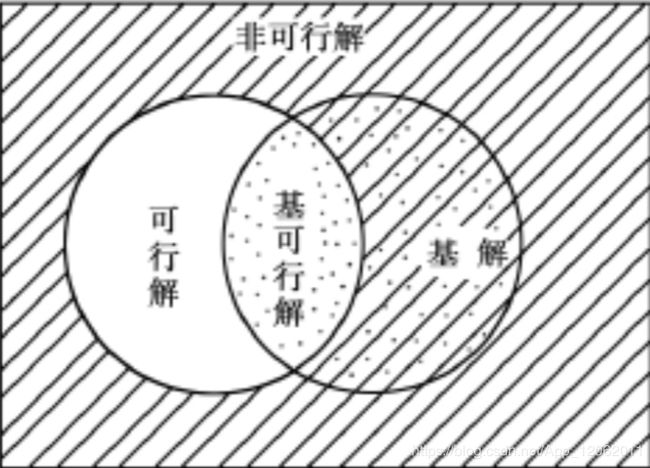
对应于基可行解的基 , 称为可行基。约束方程组(1-5)具有基解的数目最多是 Cnm （组合）个。一般基可行解的数目要小于基解的数目。以上提到 的几种解的概念, 它们之间的关系可用下图表明。另外还要说明一点 , 基解中的非零分量的个数小于m 个时, 该基解是退化解。在以下讨论 时 , 假设不出现退化的 情况。以上给出了线性规划问题的解的概念和定义 , 它们将有助于用来分析线性规划问题的求解过程。

三、相关方程解法

1、图解法，画出可行域，这个可以进行编程进行实现、

2、直接使用MATLAB的相关方法进行解题、

[x,fval]=linprog(c,A,b,Aeq,beq,LB,UB,Xo,OPTIONS)

     其中fval返回的是目标函数的值，然后x则是返回取到fval时x的对应的值，然后LB和UB是对应x的上界和下界（可以省略），x0是x的初始值（暂时可以忽略）

OPTIONS是控制参数。

其他还有专门的线性规划求解算法，后面单独介绍。

四、一些其他问题转换成线性规划

1、绝对值之和最小

在这里我们就可以令，就可以满足，这样子这个问题就变成了

2、两个数的差的绝对值，在xi固定时，取得max，之后在去定yi

我们取，就可以转换问题了

五、一些线性规划可以解决的实际问题

1、生产力有限，要求取得最大收益，更一般性的说法，是资源分配模型，用来解决在资源有限的情况下，如何将资源分配给彼此竞争的需求，从而实现资源的优化配置。

2、运输问题（产销问题）

      要求运输费用最小

          在这里需要记得有一个很重要的等式，就是所有产地送出去的等于所有销售地收到的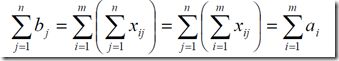

3、指派问题

     要求花费的工作时间要最短

             

（2）求解指派问题的匈牙利算法、

     首先我们要知道对与系数矩阵C由这样的性质，同时对每一行（列）加上或者减去同样的一个数，得到的新矩阵和原矩阵的指派问题具有相同的最优指派。

一般步骤是：

a、每行每列消除最小的数字，使得出现能够出现N(与矩阵大小相同）个位于不同行不同列的零元素，选定就是最优解。

b、如果上一步骤没办法直接完成，则、

4、对偶理论（与反函数相比较）

最重要的是掌握其性质，可以用来检验是不是最优解、、

5、投资的收益和风险（主要多目标函数如何并成一个目标函数）

      下一步主要是设立变量（这是数学建模中一步很关键的地方，你指标选的好，方程就好列好解，否则。。。。）

      之后就是加入限定，一些理想化的假设

      然后写出方程

     其中第一个目标函数为收益，第二个为风险。

     下一步就是化简目标函数

（1）固定风险水平，优化收益

（2）固定盈利水平，极小化风险

（3）同时考虑两个，这样的话需要加入一个权重s。

6.混料模型

资源分配模型是将各种资源分配给不同的需求，混料模型是把零散的资源整合起来，简而言之，混料模型解决的是决策各种成分的组合以最好的满足生产的需要。

7.运营规划模型

用以决策生产工作的安排以有效的使用可用资源。

8.排班和人员规划模型

在工作量给定的前提下，我们需要规划完成这些工作的资源投入，特别的，我们必须决定不同类型的员工人数和排班数量，以保证完成所有的工作量。

9.多阶段模型

用来建模动态的，随时间变化的，或者多个时间段执行的。