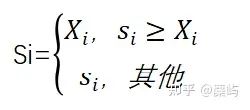2023数模国赛C 题 蔬菜类商品的自动定价与补货决策-完整版创新多思路详解（含代码）

题目简评：看下来C题是三道题目里简单一些的，考察的点比较综合，偏数据分析。涉及预测模型和运筹优化(线性规划)，还设了一问开放型问题，适合新手入门，发挥空间大。

题目分析与思路：

背景：在生鲜商超中，一般蔬菜类商品的保鲜期都比较短，且品相随销售时间的增加而变差， 大部分品种如当日未售出，隔日就无法再售。因此，商超通常会根据各商品的历史销售和需求情况每天进行补货。

由于商超销售的蔬菜品种众多、产地不尽相同，而蔬菜的进货交易时间通常在凌3:00-4:00，为此商家须在不确切知道具体单品和进货价格的情况下，做出当日各蔬菜品类的补货决策。蔬菜的定价一般采用“成本加成定价”方法，商超对运损和品相变差的商品通常进行打折销售。可靠的市场需求分析，对补货决策和定价决策尤为重要。从需求侧来看，蔬菜类商品的销售量与时间往往存在一定的关联关系；从供给侧来看，蔬菜的供应品种在 4 月至 10月较为丰富，商超销售空间的限制使得合理的销售组合变得极为重要。

附件 1 给出了某商超经销的 6 个蔬菜品类的商品信息；

附件 2 和附件 3 分别给出了该商超 2020 年 7 月 1 日至 2023 年 6 月 30 日各商品的销售流水明细与批发价格的相关数据；

附件 4 给出了各商品近期的损耗率数据。

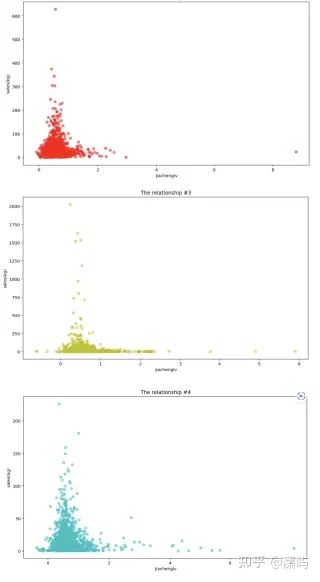
问题一：蔬菜类商品不同品类或不同单品之间可能存在一定的关联关系，请分析蔬菜各品类及单品销售量的分布规律及相互关系。

思路概要：该问需要我们利用附件1和附件2中给出的数据进行数据分析，计算各品类销量以及各单品销量的相关系数以判断相关关系，进行合理的回归拟合以进一步判断具体的相互关系。同时该问可以进行丰富的可视化操作（如热力图、频率图、分布图、回归拟合图等）。

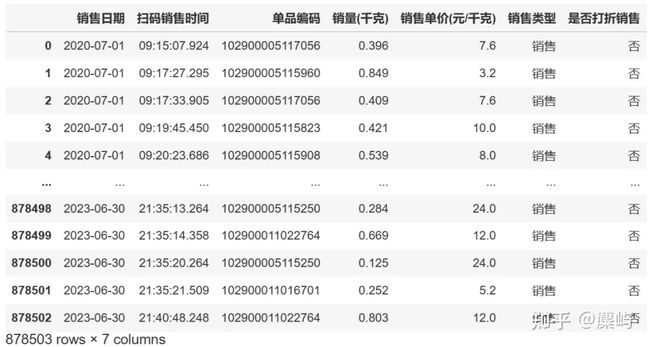
思路详解：首先提取附件1附件2中的相关变量进行初步的数据查看：(代码使用python，软件为Jupiter）

import pandas as pd
import numpy as np
df1=pd.read_excel('附件1.xlsx')
df2=pd.read_excel('附件2.xlsx')
print(df2)
print(df2)   

Df1：

Df2：

对于海量数据的dataframe表格，需要首先进行空白值检查。

print(np.any(df1.isnull()))  # 只要有一个空值便会返回True，否则返回False
print(np.any(df2.isnull()))  # 只要有一个空值便会返回True，否则返回False    

输出结果为：

False，False

故不存在缺失值，可以直接进行分析。

·首先针对附件2的数据，分析各单品的销售量数据分布规律。

由于数据集为各单品的明细数据，需要进行同单品合并：

single_item=df2['单品编码'].unique().tolist() #记录不重复的单品编码
df_singlesales=pd.DataFrame(columns=['单品编码','销量'])#创建新的空dataframe
for item in single_item:
    sales=df2[df2['单品编码']==item]['销量(千克)'].sum()
    df_singlesales.loc[len(df_singlesales)] = [item, sales]
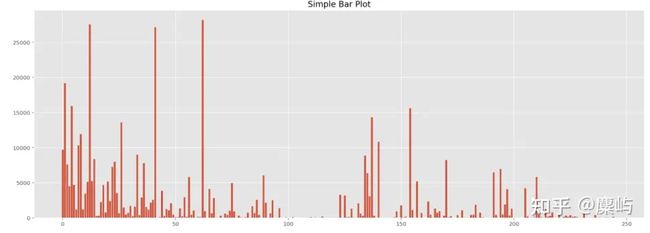
print(df_singlesales)   

直接对各个单品的销量分布进行可视化：

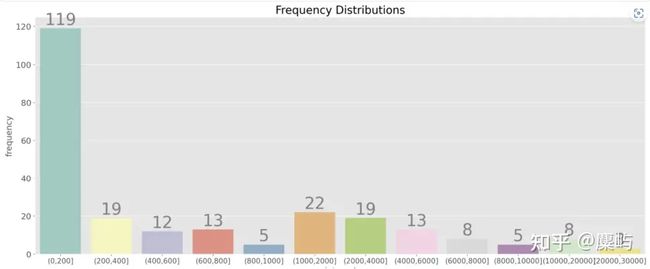
于数据集的数量巨大，难以直接进行数据统计分析规律，不妨针对销量列数据的数据范围进行合理的数值分组，针对每个区间的单品数目进行统计，以归纳销售数据的分布规律。

接着针对附件1给出的品类进行合并分析：

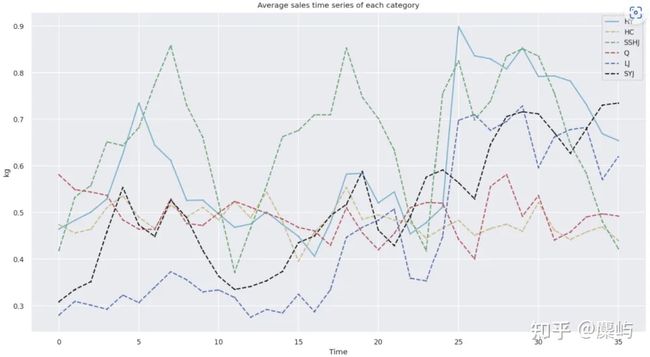
·在探究完各单品及品类销售量的分布规律之后，还需要分析之间的相互关系。

比较重要的是6个品类的销售数据相关关系。想要分析数据相关关系，需要建立相关的时间序列。

问题2：考虑商超以品类为单位做补货计划，请分析各蔬菜品类的销售总量与成本加成定价的关系，并给出各蔬菜品类未来一周(2023 年 7 月 1-7 日)的日补货总量和定价策略，使得商超收益最大。

思路概要：该问需要我们利用附件2和附件3中给出的数据进行数据分析，合并同品类以及同日期的销售数据，并分析品类内销量与定价（加成率）的关系，根据分析结果选择适当的模型（线性、二次等）进行拟合，注意不同品类应存在不同的拟合关系。在得到具体的销量与成本加成定价关系之后，需要根据历史销售流水数据预测出未来一周的销量（预测方法可以采用任意的时间序列预测方法），并根据预测的销量和得到的销量定价关系制定合适的定价策略，获得最大收益。

思路详解：成本加成定价法公式是指： 定价=基本成本×（1+加成率）......

散点图

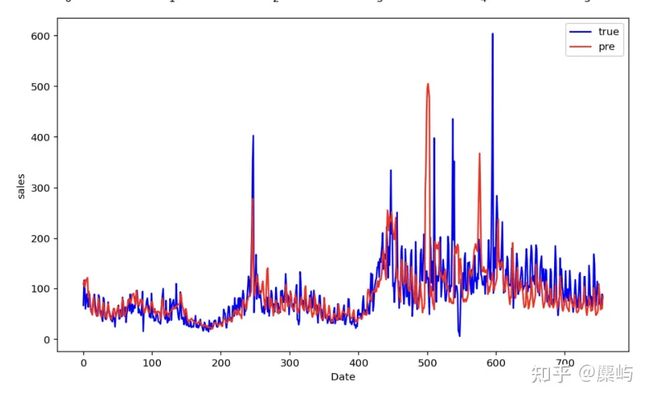
LSTM预测

问题三：因蔬菜类商品的销售空间有限，商超希望进一步制定单品的补货计划，要求可售单品总数控制在 27-33 个，且各单品订购量满足最小陈列量 2.5 千克的要求。根据 2023年 6 月 24-30 日的可售品种，给出 7 月 1 日的单品补货量和定价策略，在尽量满足市场对各品类蔬菜商品需求的前提下，使得商超收益最大。

思路概要：该问需要我们在给定的各项约束限制下，构建非线性规划模型，求取最大收益。其中问题三给出了各项约束，问题二中得到的各品类销量与加成率关系函数作为给定定价策略下的实际销量计算函数。

首先求出2023年6.24-6.30的可销售商品种类，记为集合Cavailable：

import pandas as pdimport numpy as npdf2=pd.read_excel('附件2.xlsx')C_available=df2[(df2['销售日期']>='2023-06-24')&(df2['销售日期']<='2023-06-30')&(df2['销售类型'])]['单品编码'].unique().tolist() #6.24-6.30可销售品种n=len(C_available)#可销售单品数目

其中n为集合的元素数目，也即可销售的商品种类个数。

求得为49，而实际需要限制出售总个数m∈[27,33] （1）。

设每个单品进货量为Xi，i=1,2,3，...m

有Xi≥2.5（2） 每个单品的编号IDi∈Cavailable （3）

（1）（2）（3）构成了本题的约束条件

设每个单品的 加成率为αi，则对应单品的六个种类，加成率与最大销量的关系：

F1（s）=α 花叶类

F2（s）=α 花菜类

F3（s）=α 水生根厥

F4（s ）=α 茄类

F5（s）=α 辣椒类

F6（s）=α 食用菌

设实际销量为Si，则Si的计算规则 如下：

代码：......

问题四：为了更好地制定蔬菜商品的补货和定价决策，商超还需要采集哪些相关数据，这些数据对解决上述问题有何帮助，请给出你们的意见和理由。

思路概要：该问需要我们进一步探讨问题，通过补充相关数据的方法来使得补货与定价策略更加完善。这里需要重点考虑前述解题中没有使用到的数据，如损耗率(%)以及打折的情况。其次，题目中提到的商品空间也并没有给出实际的库存限制信息（问题3只给出了限制的单品数目，并没有给出具体的可承受库存空间）。

可以从问题1~3的计算过程入手，查看每个计算过程是否还可以利用其他的可获得的数据。

完整思路代码已整理好，见网pan链接，如失效请私信~

链接：https://pan.baidu.com/s/1_Rmh1UZS6uuM_ETvMVC5EA 提取码：n64s