LeetCode 514. Freedom Trail

一、题目描述

In the video game Fallout 4, the quest “Road to Freedom” requires players to reach a metal dial called the “Freedom Trail Ring”, and use the dial to spell a specific keyword in order to open the door.

Given a string ring, which represents the code engraved on the outer ring and another string key, which represents the keyword needs to be spelled. You need to find the minimum number of steps in order to spell all the characters in the keyword.

Initially, the first character of the ring is aligned at 12:00 direction. You need to spell all the characters in the string key one by one by rotating the ring clockwise or anticlockwise to make each character of the string key aligned at 12:00 direction and then by pressing the center button.

At the stage of rotating the ring to spell the key character key[i]:

1. You can rotate the ring clockwise or anticlockwise one place, which counts as 1 step. The final purpose of the rotation is to align one of the string ring’s characters at the 12:00 direction, where this character must equal to the character key[i].
2. If the character key[i] has been aligned at the 12:00 direction, you need to press the center button to spell, which also counts as 1 step. After the pressing, you could begin to spell the next character in the key (next stage), otherwise, you’ve finished all the spelling.

Example:

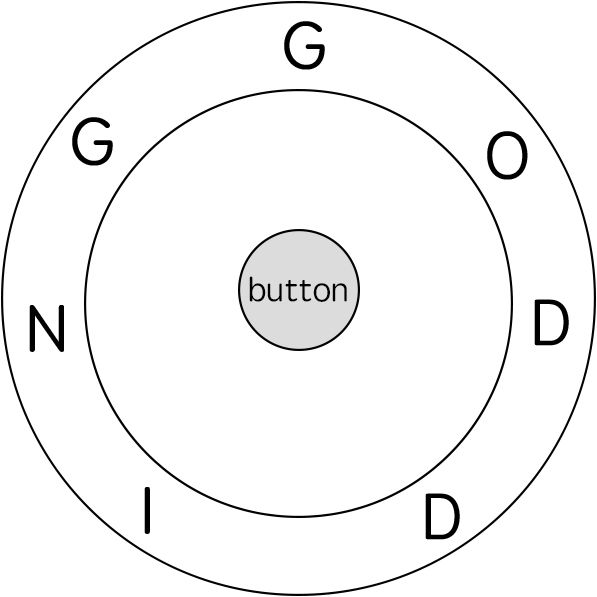
Input: ring = “godding”, key = “gd”
Output: 4
Explanation:
For the first key character ‘g’, since it is already in place, we just need 1 step to spell this character.
For the second key character ‘d’, we need to rotate the ring “godding” anticlockwise by two steps to make it become “ddinggo”.
Also, we need 1 more step for spelling.
So the final output is 4.

Note:

1. Length of both ring and key will be in range 1 to 100.
2. There are only lowercase letters in both strings and might be some duplcate characters in both strings.
3. It’s guaranteed that string key could always be spelled by rotating the string ring.

 

---

 

二、题目分析

  根据题意，我们需要使用给出的 ring 字符串拼出目标 key 字符串，求出所需的操作步数。虽然按题目所说，按下按钮即 spell 也算一个操作步数，但这部分总的步数就是 key.size() ，在最后加上即可，所以以下讨论就忽略这个步骤。

  顾名思义，我们可以将 ring 字符串看成一个简单的环形图，从一个字符转到其他字符所需操作步数即为它们之间的距离，这里用 $a_i{b}_j$ 表示 ring 中其中一个 a 字符到其中一个 b 字符的距离；并使用 $abc$ 表示拼成 "abc" 字符串所需的最小操作数。
  为了方便说明，这里暂且使用字符串 "abcd" 作为 key。考虑到最初的起点 ring[0] ，用 X 来代表，则 key 为 "Xabcd" 。

  先来看 key 的前两个字符 Xa，若我们要求拼成它的最小操作数，那么很简单，只要取 $Xa=min(X{a}_0,X{a}_1,X{a}_2,...,X{a}_n)$ 即可。
  若我们再加上第三个字符 b ，在 ring 中有n个字符 b 的情况下，我们分两步操作，①对于每一个“终点” $b_i$ ，求出从 X 出发到达该位置的 b 字符的距离，②再从它们之中选出一个最小的即可。在步骤①中我们要使用到 $X{a}_0,X{a}_1,...,X{a}_n$ 的数据，即到 $b_i$ 的距离为 $min(X{a}_0+a_0{b}_i,X{a}_1+a_1{b}_i,X{a}_2+a_2{b}_i,...,X{a}_n+a_n{b}_i)$，表示为 $Xa{b}_i$ ，最后在这些最小值之中再求它们的最小值即可，即 $Xab=min(Xa{b}_0,Xa{b}_1,...,Xa{b}_n)$ 。
  同理，若再加上第四个字符 c ，①对于每一个“终点” $c_i$ ，求出从 X 出发到达该位置的 c 字符的距离，②再从它们之中选出一个最小的即可。而在步骤①中同样要用到 $Xa{b}_0,Xa{b}_1,...,Xa{b}_n$ 的数据，即到 $c_i$ 的距离为 $Xab{c}_i=min(Xa{b}_0+b_0{c}_i,Xa{b}_1+b_1{c}_i,Xa{b}_2+b_2{c}_i,...,Xa{b}_n+b_n{c}_i)$ 。
  最后一个字符也是相同步骤，不再赘述。最终我们就可求得需要的 $Xabcd$ 。

  从以上分析可看出，这是一个自底向上的动态规划问题。对于其他字符串，也是相同的步骤求解。

 

---

 

三、具体实现

  按照分析，总的复杂度为$O(N{L}^2)$ ，其中 $N$ 为 key 的长度，$L$ 为 ring 的长度。
  使用哈希表 unordered_map 存储 ring 中各个字母的下标（同个字母的不同位置），使用 vector> 存储类似 $X{a}_0,X{a}_1,...,X{a}_n,Xa{b}_0,Xa{b}_1,...,Xa{b}_n$ 这些数据。

class Solution
{
  public:
    int findRotateSteps( string ring, string key )
    {
        int **distance = new int*[ring.size()];
        for ( size_t i = 0; i < ring.size(); ++i )
            distance[i] = new int[ring.size()]();

        for ( int i = 0; i < ring.size(); ++i ) {
            for ( int j = 0; j < ring.size(); ++j ) {
                distance[i][j] = abs( j - i );
                if ( distance[i][j] > ring.size() / 2 )
                    distance[i][j] = ring.size() - distance[i][j];
            }
        }

        unordered_map<char, vector<int>> indexTable;
        for ( size_t i = 0; i < ring.size(); ++i )
            indexTable[ring.at( i )].push_back( i );

        vector<unordered_map<int, int>> result( key.size() );
        for ( int n : indexTable.at( key.at( 0 ) ) ) {
            result[0][n] = distance[0][n];
        }

        int minStep = INT_MAX;

        for ( size_t i = 1; i < key.size(); ++i ) {
            for ( int n : indexTable.at( key.at( i ) ) ) {

                int thisMin = INT_MAX;
                for ( auto p : result.at( i - 1 ) ) {
                    thisMin = min( thisMin, p.second + distance[p.first][n] );
                }
                result[i][n] = thisMin;

                if ( i == key.size() - 1 )
                    minStep = min( minStep, thisMin );

            }
        }

        for ( size_t i = 0; i < ring.size(); ++i )
            delete [] distance[i];
        delete [] distance;

        return minStep + key.size();
    }
};