如何用分布式Pollard-Rho法对椭圆曲线离散对数问题（ECDLP）进行攻击（下）

 在上一篇中，我主要介绍了对赛题的初步攻击——单机Pollard-Rho。接下来介绍分布式算法。
 让多个机子，从点集合G中不同的起点进行出发，用QD法记录的桩点会被记录到一个公共表里，然后每个机子共享数据，也就是说每个机子可以知道一个桩点，是否曾经被自己或者其它机子产生出来过。
 这里面有一些隐含的信息。首先，并不是有n台机子，产生答案的时间就会缩短到原来的1/n，事实上，随机产生的Rho图数量非常巨大，基本上而言每个起点会落在不同的Rho图中，然后产生答案的时间会是它们各自工作的最小值。这样的话分布式意义就不会很大。因此有不少人提出了更好的迭代函数，以及提出迭代一定步数后重新开始，增加起点落在相同图中的概率。
 这方面的理论，我拿捏得并不是很清楚，因此只是保守地去实现基本化的分布式Rho法，至于改进，可以交给各位读者了。
 接下来是需要一个类似分布式的解决方案。一开始完全不了解这一块，开始学习hadoop，不过难度太大放弃了，而且像是杀鸡用牛刀的感觉。之后查了很多资料也百思不得其解。后来向一位经管的学长提了这方面的需求问题，他向我建议了Redis（太感谢了），Redis是一个比较傻瓜式的软件。它支持在一个服务器上部署Redis的Server服务，对一些诸如列表，集合，映射进行记录，然后多个Client可以访问服务器，对这些记录进行修改和查询。
 Redis相关的命令网络上资料已经很丰富，不再详述。
 使用Redis的一个好处是很方便，弱点在于毕竟是通过网络交互，速度会比真正的分布式集群要慢，当然成本也就更小啦。考虑到我们效率的瓶颈并不是在于映射表的修改和查询，因此我觉得Redis是一个完全可以接受的方案。
 第二个问题是选机子。根据我的估计，无论在阿里云，腾讯云还是其他的平台上租机子都是一笔可怕的开销（穷人的哀伤）。我产生了一个大胆的想法，只租用搭载Redis的服务器，而运算端则可以靠身边有心人们发动自己的算力进行支持。因此我选择了在华为云上租了一个Redis3.0的单机，存储是2GB，由于是新用户正好是免费的。注：当时只有Redis3.0能用购买的弹性公网IP，使得外网能够访问这个服务器，更高版本的Redis只能从华为云内部的机子来访问了。
 又遇到了一个小难题，Redis对于C++的API似乎不是很友好，我花了一阵子又去下载了国人开发的一个网络框架库ACL（万分感谢）https://www.oschina.net/news/60340/ace-redis-cpp，学习了一下，终于能够用C++来操纵Redis了。给出运算端源代码。

//Milo: 正式程序
#include
#include
#include "lib_acl.hpp"
#include "ecn.h"
using namespace std;

const int sz = 2;
const int csz = 3;
const int check_mod = 100003;

Miracl precision(20, 0);
miracl *mip = &precision;
Big mo = "604462909807314587353111";
Big a = mo-3;
Big b = 95;
Big r = "604462909807750541909849";
Big A1, B1, A2, B2, x, y;
ECn P, R, Fm;
ECn stp[sz];
Big da[sz], db[sz];
Big seeda = "1655165156177", seedb = "384864864613";

acl::redis O;
char bufx[200], bufy[200];
int len;
big temp = mirvar(0);

inline int Block(ECn &num)
{
	num.getx(x);
	return x[0] % csz;
}

inline void F(Big &A, Big &B, ECn &Tmp)
{
	register int i = Block(Tmp);
	if (i < sz)
	{
		A += da[i];
		B += db[i];
		Tmp += stp[i];
	}
	else
	{
		A <<= 1;
		B <<= 1;
		Tmp += Tmp;
	}
	if (A >= r)
		A -= r;
	if (B >= r)
		B -= r;
}

inline bool check(ECn &Fm)
{
	Fm.getx(x);
	return x[0] % check_mod == 0;
}

//向Redis映射表中插入内容
//注意映射表只支持字符串，所以先解析字符数组里，然后再调用set函数

inline void insert(ECn &key, Big &va, Big &vb)
{
	len = cotstr(va.getbig(), bufx), bufx[len] = ' ';
	cotstr(vb.getbig(), bufx + len + 1);
	key.getxy(x, y);
	len = cotstr(x.getbig(), bufy), bufy[len] = ' ';
	cotstr(y.getbig(), bufy + len + 1);
	O.set(bufy, bufx);
	O.clear();
}

//如果发现桩点，那么在映射表中查询，如果无则返回false，有则返回true，同时求出表中点对应的A,B系数

inline bool count_and_query(ECn &c)
{
	c.getxy(x, y);
	len = cotstr(x.getbig(), bufx), bufx[len] = ' ';
	cotstr(y.getbig(), bufx + len + 1);
	if (!O.exists(bufx))
	{
		O.clear();
		return false;
	}
	acl::string val;
	O.get(bufx, val);
	O.clear();
	char *res1 = val.c_str(), *res2 = res1;
	while (*res2 != ' ')
		++res2;
	*res2 = '\0';
	cinstr(temp, res1);
	A2 = temp;
	cinstr(temp, res2 + 1);
	B2 = temp;
	return true;
}

Big pollard_rho()
{
	register long long cnt = 0, msz = 0;
	for (;; F(A1, B1, Fm))
	{
		normalise(Fm);
		if (check(Fm))
			if (count_and_query(Fm))
			{
				if (B1 != B2)
					break;
				A1 = rand(r);
				B1 = rand(r);
				Fm = mul(A1, P, B1, R);
			}
			else
				insert(Fm, A1, B1);
		if (++cnt % 100000 == 0)
		{
			cout << "step " <<cnt / 100000<< ':' << A1 << ' ' << B1 << ' ' << Fm << ' ' << endl;
			//每100000步检测一次是否有人已经发现了答案
			if (O.scard("$"))  //注意，网络中断时，一段时间后同样也会变成true
			{
				O.clear();
				return Big(-1);
			}
			O.clear();
		}
	}
	return moddiv(A2 - A1 + r, B1 - B2 + r, r);
}

int main()
{
	ios::sync_with_stdio(false);
	cout << "Start your chasing...Hope you're lucky enough!" << endl;
	ecurve(a, b, mo, MR_PROJECTIVE);
	P = ECn("428432040100075198254744", "95025782588400118295756");
	R = ECn("472138605558837378507194", "138148835226095728614736");

	irand(time(0));
	for (int i = 0; i < sz; i++)
	{
		da[i] = !i ? seeda : pow(da[i - 1], 2, r);
		db[i] = !i ? seedb : pow(db[i - 1], 2, r);
		stp[i] = mul(da[i], P, db[i], R);
		cout << stp[i] << endl;
	}
	A1 = rand(r);
	B1 = rand(r);
	Fm = mul(A1, P, B1, R);
	cout << "Your initial point is " << Fm << endl;
	mip->IOBASE = 64;  //传送信息是Base-64，尽量减少网络传输字节量

	acl::acl_cpp_init();  //这个函数一定要调用！，一开始一直没写，被坑了好久。
	const char* redis_addr = "*******:6379";  //这里面填写的是当时的公网IP地址
	int conn_timeout = 10, rw_timeout = 10;  //时间延迟上限
	acl::redis_client conn(redis_addr, conn_timeout, rw_timeout);
	conn.set_password("********");//"这里面填写的是当时服务器的访问密码"
	O.set_client(&conn);
	O.clear();

	long long sta = clock();
	Big result = pollard_rho();
	mip->IOBASE = 10;
	if (result > -1)
	{
		cout << "Ans: " << result << " Congratulations!" << endl;  //求出答案
		cotstr(result.getbig(),bufx);
		O.sadd("$", vector<acl::string>{bufx});  //向服务器，写入答案，“$”是答案标志符号，作为新建集合名
		O.clear();
	}
	else
		cout << "Sorry, the answer has been dug by others. Thanks for your joining." << endl;
	cout << (double)(clock() - sta) / CLOCKS_PER_SEC << endl;
	conn.close();
	getchar(), getchar(), getchar();


	//check
	//cout <<(Big)"151136586324959103432352"*P;
	return 0;
}

 基本机制就是每个机子从随机起点开始奔跑，（注意，此时迭代步进应该统一，要不然不同机子图的结构都不一样了），（不统一或许也可以？），然后如果有人找到对撞，就会往服务器发送标记符号和答案，此时每100000步每个终端检测一次是否有人发现答案，有则立即退出，不用继续迭代。
 我们的期望是，轻微有偿地利用个人闲置算力，所以，如果有人发现了Ans，可以向联系我们汇报，此时正确答案已经发送到我们手中，我们只需两相比较，即可对发现者进行奖励。（哇咔咔被自己聪明了一次）。
 后来发现一个小bug，如果断网的话，一段时间后也会显示“Sorry, the answer has been dug by others. Thanks for your joining.”这句话。后来我只好通知大家，找到答案我们会有信息，请大家重新运行。（忽然发现这样也是间接达到了运行一段时间后从新起点出发的效果？！）
 程序本身不难理解，但是测试和调试真是花了我不少心血。首先因为对库的不了解，调试通已经很不容易。接着是对之前的小数据进行尝试，估计运行的时间以及调整各个参数的大小。最后对第二级别的数据尝试跑了一下，当时在小班群里向大家解释了我们的工作，鼓励大家帮忙运行终端。当时持续运行的机子大概七八台吧，三个多小时之后成功找到了答案并且成功验证（小插曲：一开始还以为答案错了，调了一晚上bug，发现是自己之前的答案弄混了，WTF）。
 做了最后的细致检查，包括效率和网络流量之后，我花了一天写了一份文案。如下：




 可以看出很沙雕和中二。当然当时目的是吸引人，所以言辞夸张一点可以理解。
 接下来截图几张我当时的朋友圈。

 可以说这些文案的画风几乎有点毁我本人的形象了QwQ。
 通过在各种各样的群里的广泛宣传，以及同学帮忙的推广。一开始参与的同学还是挺多的，但是一两天之后就逐渐热情减退。其实也可以理解，于是我就专门负责给大家每天加油打气，鼓励大家发动各自身边的人来参加进来，充满希望不要放弃。但其实我当时也没有底气，毕竟从来没有要等待过这么长时间。一开始还乐观估计了一阵，到第四天之后心里就觉得压力越来越大。在和群里的同学们乐呵呵地相处时，别提有多担心。有两次做梦都梦到朋友找到答案来向我报喜，梦醒来之后又觉得很无奈。
 中途2G的Redis不够用，只好花了七十块钱给2G扩容成4G。其实真的感谢大家，扩容的时候所有终端都下线了，当我说更新完毕的时候，大家又纷纷主动地运行上来。
 在人数比较少的时候，我也不得不花钱买了一些云主机帮助运算。
 基本上平均情况下会在20个终端昼夜持续不停运算，白天最多可以达到四十多个。其中一位学弟，除了扩容那一次之外甚至就没有停下来过。
 终于到了第六天，我们的努力没有白费。
 感觉我那一刻是真正的幸福

 当时真的感觉超级幸福！
 一个遗憾：不知为何，求出解的同学一直没能联系我。最后只好把红包砸给群友了2333。

---

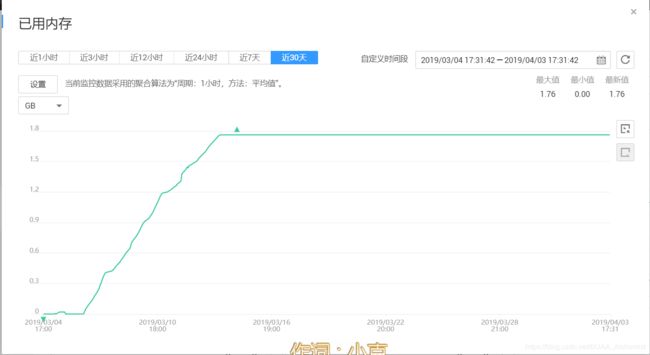
 总计一万一千亿次单步迭代，Redis存储数据达到1.76G，找到了答案。

 然而，因为某些原因，我们无法有进一步进展。
 主要原因是，我对于底层优化不得要领，Miracl库的文档中叙述如何采用comba等方法来得到一个更快速的库，但尝试多次均失败，另外的尝试包括在linux环境下运行，通过__int128作为基础类型等等。也尝试过学习汇编，不了了之。
 另外，队友对于比赛也不是很上心。其实三组数据，我专攻的Pollard-Rho法主要会针对第三组，而前两组属于有一些特征的椭圆曲线，应该是用其他特殊算法来攻击的。但他们最后也因为阅读不懂得论文放弃了。
 因此，后来虽然老师对于我们的阶段性成果很欣喜，一段时间后也就逐渐失望了。我们最后也放弃了本次比赛。
 但总的来说，这次经历还是让我提高了很多，尤其是设计分布式Pollard-Rho法，这可以说是这学期我写过的比较自豪的一段代码。

 附：已得到的答案

第一部分
139189752582973
7989691388346524583
第二部分
9102849376754
460749542374704902
第三部分
58891866538906
3504954937854331487
151136586324959103432352