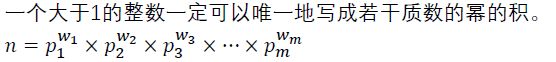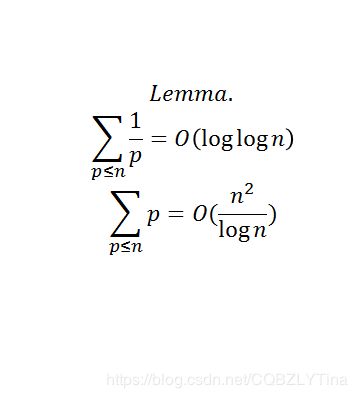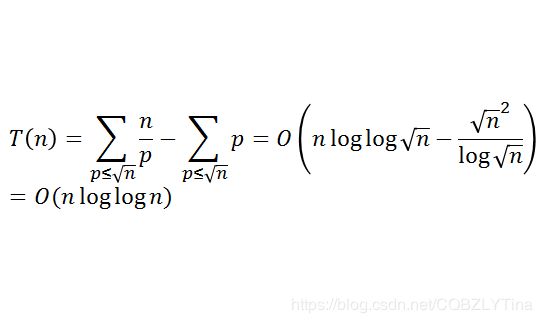数论---整除与素数---筛法（素数筛，约数个数筛，约数和筛）

素数定理

整数的标准分解（唯一分解）

#include
int p[105],w[105],k;
void factorize(int n)
{
	for(int i=2;i*i<=n;i++)
		if(n%i==0)
		{
			p[++k]=i;
			while(n%i==0)
				n/=i,w[k]++;
		}
	if(n!=1)
		p[++k]=n,w[k]=1;
}
int main()
{
	int n;
	scanf("%d",&n);
	factorize(n);
	for(int i=1;i<k;i++)
		printf("%d^%d*",p[i],w[i]);
	printf("%d^%d",p[k],w[k]);
}

互质：

互质（Coprime）：两个数没有公共的因数（除1以外），则这两个数互质。
将互质的两个数分别唯一分解后，两个积式中不会出现相同的质数。

gcd与lcm

gcd与lcm

积性函数

例题 codevs6899倒数和分解

这里有个在数学上比较常用的操作 当a-n的形式出现在分母 不好操作，可以进行还原

关于“一一对应”的理解：n已知，是常数，而要使等式成立，显然不存在一个b的取值时有多个a，所以一定是一一对应的。

※筛法(Sieve Method)※

主要有两类：埃拉托斯特尼筛法（埃筛）和欧拉筛（线性筛），相对来说，欧拉筛的效率更高但理解起来相对困难一点。

埃筛

埃筛是用一个数组标记是否为素数，然后依次筛去这个素数的倍数，代码也比较好理解。

bool sieve()
{
	for(int i=2;i<=n;i++)
		if(!vis[i])
		{
			prime[++pn]=i;
			for(int j=i*i;j<=n;j+=i)
				vis[j]=1;
		}
}

值得一提的是，第11行的for循环可以从i * i开始而非i * 2（算是一个小优化）吧，因为i * 比i小的数的情况已经在之前的那个数处理过了

比如说i== 7时，可以从7 * 7开始 因为6 * 7,5 * 7的情况都已经分别在i ==6和i ==5的情况中被处理过。

---

时间复杂度的分析

显然，一些数被重复筛去，所以不是线性的。

---

筛约数个数，约数和

bool sieve()
{
	for(int i=1;i<=n;i++)
		for(int j=i;j<=n;j+=i)
			d[j]++,s[j]+=i;
}

欧拉筛

在埃筛的基础上，让每一个合数都只被他的最小质因子筛去，从而减小时间。

先看一波代码

bool sieve()
{
	for(int i=2;i<=n;i++)
	{	
		if(!vis[i])
			prime[++pn]=i;
		for(int j=1;j<=pn&&prime[j]*i<=n;j++)
		{
			vis[i*prime[j]]=1;
			if(i%prime[j]==0) break;
		}
	}
}

理解

关于vis[i * prime[j]]=1的理解：
这里不是乘上i的多少多少倍，而是把prime数组里面的所有质数当做i * prime[j]的最小质因子来做 也就是消去这个质数的i倍

关于if(i%prime[j]==0) break;的理解：
如果满足i%prime[j]==0，设i=prime[j]*k
那么下一次j++的时候 我们就会筛去s=prime[j+1] ＊i=prime[j+1] * prime[j] * k ，而这与我们想要让每个数都被他的最小质因子筛去的愿望不符合，因为这个数会在i=prime[j+1]*k 的时候被筛去。

综上，我们可以发现，i*prime[j]的最小质因子为prime[j]，当i%prime[j]时，由于prime数组是有序的，i的最小质因子也是prime[j]

欧拉筛求约数个数

$d(n)$表示n的约数个数（约数个数函数）
我们先复习一下约数个数的计算方法
$n=p_1^{w_1}{p}_2^{w_2}{p}_3^{w_3}\cdot \cdot \cdot p_m^{w_m}$
$d(n)=(w_1+1)(w_2+1)(w_3+1)\cdot \cdot \cdot (w_m+1)$
满足$d(n)=d(p_1^{w_1})d(p_2^{w_2})d(p_3^{w_3})\cdot \cdot \cdot d(p_m^{w_m})$，显然d(n)是积性函数

以下$i$的意义与上文的欧拉筛中的$i$意义相同，从2到n进行枚举 我们新定义一个$num[i]$表示i的最小质因子的次数
显然$d[1]=1$
分类讨论如下：
①若i是素数 $d[i]=2$
②若$i\%prime[j]̸=0$
i不包含prime[j] i*prime[j]只含有prime[j]的一次方
我们之前已经得到了d[i] 现在加入prime[j]这个新的因子即可

---

$d[i\ast prime[j]]=d[i]\ast 2$
$num[i\ast prime[j]]=1$

---

③若$i\%prime[j]=0$
i包含prime[j]的至少一次方
并且i的最小质因子就是prime[j]
相当于$i\ast prime[j]$跟$i$比起来，就是多了一个最小质因子
$d[i]=(num[i]+1)(w_2+1)(w_3+1)\cdot \cdot \cdot (w_m+1)$
$d[i\ast prime[j]]=(num[i]+1+1)(w_2+1)(w_3+1)\cdot \cdot \cdot (w_m+1)$
所以

---

$d[i\ast prime[j]]=\frac{d[i]}{num[i]+1}\ast (num[i]+2)$
同时，不难看出num的更新：$num[i\ast prime[j]]=num[i]+1$

---

int d[MAXN],prime[MAXN],num[MAXN],vis[MAXN],pn;
void sieve(int n)
{
	d[1]=1;
	for(int i=2;i<=n;i++)
	{
		if(!vis[i])
		{
			prime[++pn]=i;
			num[i]=1;
			d[i]=2;
		}
		for(int j=1;j<=pn&&i*prime[j]<=n;j++)
		{
			vis[i*prime[j]]=1;
			if(i%prime[j]==0)
			{
				num[i*prime[j]]=num[i]+1;
				d[i*prime[j]]=d[i]/(num[i]+1)*(num[i]+2);
				break;
			}
			d[i*prime[j]]=d[i]*2;
			num[i*prime[j]]=1;
		}
	}
	
}

欧拉筛求约数和

首先我们还是先复习一下约数和的计算方法
$$n=p_1^{w_1}{p}_2^{w_2}{p}_3^{w_3}\cdot \cdot \cdot p_m^{w_m}$$
$$s(n)=(1+p_1+p_1^2+\cdot \cdot \cdot +p_1^{w1})(1+p_2+p_2^2+\cdot \cdot \cdot +p_2^{w2})(1+p_3+p_3^2+\cdot \cdot \cdot +p_3^{w3})\cdot \cdot \cdot (1+p_m+p_m^2+\cdot \cdot \cdot +p_m^{wm})$$

这个也非常好理解 我们如果把它们全部乘开，那么这个多项式的每一项都是n的一个约数

s(n)满足$$s(n)=s(1+p_1+p_1^2+\cdot \cdot \cdot +p_1^{w1})s(1+p_2+p_2^2+\cdot \cdot \cdot +p_2^{w2})s(1+p_3+p_3^2+\cdot \cdot \cdot +p_3^{w3})\cdot \cdot \cdot s(1+p_m+p_m^2+\cdot \cdot \cdot +p_m^{wm})$$，显然s(n)也是积性函数

同上，仍然定义以下$i$的意义与上文的欧拉筛中的$i$意义相同，从2到n进行枚举 我们新定义一个$psum[i]$表示关于i的最小质因子p的等比数列求和式
$1+p+p^2+p^3+\cdot \cdot \cdot +p^w$

显然$s[1]=1$
分类讨论如下：
①若i是素数 ，显然：$s[i]=i+1,psum[i]=i+1$
②若$i\%prime[j]̸=0$
则i不包含$prime[j]$ ，同上，$prime[j]$ 一定是$i\ast prime[j]$的最小质因子

$$s(i)=(1+p_1+p_1^2+\cdot \cdot \cdot +p_1^{w1})(1+p_2+p_2^2+\cdot \cdot \cdot +p_2^{w2})\cdot \cdot \cdot (1+p_m+p_m^2+\cdot \cdot \cdot +p_m^{wm})$$
$$s(i\ast prime[j])=(1+p_1+p_1^2+\cdot \cdot \cdot +p_1^{w1})(1+p_2+p_2^2+\cdot \cdot \cdot +p_2^{w2})\cdot \cdot \cdot (1+p_m+p_m^2+\cdot \cdot \cdot +p_m^{wm})\ast (1+prime[j])$$

---

则$s[i\ast prime[j]]=s[i]\ast (1+prime[j])$
$psum[i\ast prime[j]]=prime[j]+1$

---

③若$i\%prime[j]=0$
同上分析（和求约数个数的分析一样）
$$s(i)=(1+p_1+p_1^2+\cdot \cdot \cdot +p_1^{w1})(1+p_2+p_2^2+\cdot \cdot \cdot +p_2^{w2})\cdot \cdot \cdot (1+p_m+p_m^2+\cdot \cdot \cdot +p_m^{wm})$$
$$s(i\ast prime[j])=(1+p_1+p_1^2+\cdot \cdot \cdot +p_1^{w1}+p_1^{w1+1})(1+p_2+p_2^2+\cdot \cdot \cdot +p_2^{w2})\cdot \cdot \cdot (1+p_m+p_m^2+\cdot \cdot \cdot +p_m^{wm})$$

对比观察这两个式子：
$s[i\ast prime[j]]=s[i]/(1+p_1+p_1^2+\cdot \cdot \cdot +p_1^{w1})\ast (1+p_1+p_1^2+\cdot \cdot \cdot +p_1^{w1}+p_1^{w1+1})$
即：

---

$s[i\ast prime[j]]=\frac{s[i]}{psum[i]}\ast (psum[i]\ast prime[j]+1)$
$psum[i\ast prime[j]]=psum[i]\ast prime[j]+1$

---

写程序的时候可以先更新psum 再算（调整一下顺序 看起来简洁一些）

#include
#define MAXN 1005
int s[MAXN],prime[MAXN],psum[MAXN],pn;
bool vis[MAXN];
void sieve(int n)
{
	s[1]=1;
	for(int i=2;i<=n;i++)
	{
		if(!vis[i])
		{
			prime[++pn]=i;
			psum[i]=s[i]=i+1;
		}
		for(int j=1;j<=pn&&i*prime[j]<=n;j++)
		{
			vis[i*prime[j]]=1;
			if(i%prime[j]==0)
			{
				psum[i*prime[j]]=psum[i]*prime[j]+1;
				s[i*prime[j]]=s[i]/psum[i]*psum[i*prime[j]];
				break;
			}
			s[i*prime[j]]=s[i]*(prime[j]+1);
			psum[i*prime[j]]=1+prime[j];
		}
	}	
}
int main()
{
	
}

---

以下非战斗人员请撤离

完结撒花

这篇文章写了我好久啊 数论的版块确实需要多加思考
（说得好像其他版块就不需要多加思考似的（大雾
好吧 确实值得推敲的地方比较多 虽然想的时间长了点 但也还是值得
（我扯来扯去都扯了些什么啊）

---

水调数声持酒听。午醉醒来愁未醒。送春春去几时回。临晚镜。伤流景。往事后期空jx。
沙上并禽池上暝。云破月来花弄影。重重帘幕密遮灯，风不定。人初静。明日落红应满径。

---

少年何妨梦摘星，敢挽桑弓射玉衡。