背包问题基础模型深度总结-文长慎入（01背包，完全背包，多重背包）

先等一下，字多预警，密集恐惧症慎入，喂，你，就是你，小板凳搬好了吗，站久了可是会腿酸的

无节操地王婆卖瓜一下， 本文 深度好文

目录

先扯两句

0-1背包

其它类似的状态定义

1

2

小结

3  记忆化搜索

滚动数组（优化空间复杂度）

初始化

完全背包

递推关系

优化时间

滚动数组

简单有效的常数优化

多重背包

状态转移

转化为01背包问题

二进制优化

可行性问题

混合三种背包问题

最后再扯两句

 

 

---

先扯两句

本篇博文中的数组默认都从1开始。

题目说扯2句，那上一句还不够加上这一句应该够了吧。

---

0-1背包

之前写过一个0-1背包的博客，总结得还是比较清楚。0-1背包总结

0-1背包是所有背包问题的基础，在0-1背包的基础上有许多变体，许多背包问题也是由它引申而来的，所以很重要（貌似这句话才是重点）

定义dp[i][j]为前i种物品重量恰好为j的最大价值 w[i]为重量 c[i]为价值,则：

也很好理解，分别对应当前物品不取和取两种状态

当然这个状态要注意时，dp[i][j]只能转移到

其它类似的状态定义

1

定义dp[i][j]为前i件物品重量不超过j的最大价值

咦，怎么看起来跟之前的转移一模一样啊，但是这两个都是对的_(:з」∠)_

区别在于初始化的不同处理 这里先卖个关子，后面马上说 qwq

2

定义dp[i][j]为从第i个物品开始挑选重量小于j的最大价值

小结

写递推方式的dp是，不同的状态定义需要用不同的顺序，也就是规划方向。

我们在进行状态转移的时候一定要保证被用来转移的状态已经被计算过

如果顺序不好确定或者无法确定，我们可以用记忆化搜索

对，记忆化搜索，我怎么把它给忘了

3  记忆化搜索

与dp一样也需要一个数组存储 但是在函数中如果这个值已经被计算过，就直接返回 所以一般没有计算过的dp初始化为-1

以《挑战程序设计竞赛》p51-53为例

注意：在需要剪枝的情况下，可能会把各种参数都写在函数上，但是这样会使记忆化搜索难以实现

滚动数组（优化空间复杂度）

有时候数据范围比较大的时候数组会愉快地爆掉

这个时候就需要把二维数组滚成一维，但是这样就不能愉快地求方案，只能求一个答案

实际上就是开一个一维数组，每次覆盖上一行

但是这种写法j的枚举要倒序

因为如果正序的话，在状态转移的时候，会先于计算出来，就相当于中的值存储的是而不是，然后就凉凉了。

初始化

好的这就是之前卖的那个关子

先说不超过j的那个状态

对于所有的dp[0][j]都应该初始化成0，因为一件物品也不装，重量就为0，是肯定小于等于j的，状态合法，而一件也没有其价值当然也为0

再说恰好为j的那个状态

对于所有的dp[0][j]除了dp[0][0]应该初始化成0，其它都要初始化成 极小值  因为一件物品都不放的重量为0，而0是肯定不会恰好为j的，所以这个状态是不合法 的。

这个思想在dp问题中非常非常非常的重要，应当熟练掌握，很多时候差的就是这一点细节。

完全背包

其它的与0-1背包一样，完全背包的物品有无限多个。

则它对于每一件物品的决策就不止是0-1状态 还有取2件，3件……

递推关系

定义为前i种物品中取总重量不超过j的最大价值，则

k则是枚举当前物品取的件数。   

这里的k实际上是有上限的，在每个循环内 k*w[i]<=j

优化时间

以上的算法就是的时间复杂度，十分脆弱，于是我们有必要优化一下。

不难看出，选k个（k>=1）的情况与中选择k+1个的情况是相同的。（敲黑板！！！~~请记住这句话，认真理解并背诵全文）

滚动数组

有了上面的推导，一维的转移也显而易见：

和0-1背包一样？

不不不，循环顺序并不一样，完全背包的第二维是顺序枚举的

如果直接看这个方程，可以发现：顺序的枚举方式使得转移的时候第二个位置实际上是，而这个状态是取了n(n>=0)个第i件物品的状态，这次再取一件，而后面又继续枚举，就达到了取n多件的目的！

简单有效的常数优化

• 如果存在两种物品，有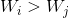而且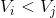，那么可以去掉物品i。这个优化的正确性显然，对于随机生成的数据，可以减小物品的件数从而提高速度，然而并不能改变最坏情况的复杂度，因为这个优化对设计过的数据可能无用，一件物品也去不掉。可以用的复杂度做这个操作，可以在输入的时候顺便做。
• 另外“背包九讲”中还有一个优化，先将物品中 w[i]>W的物品全部去掉，然后使用类似计数排序的做 法，计算出费用相同的物品中价值最高的是哪个，可以用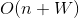来实现

多重背包

状态转移

显而易见地，我们很容易地可以想到借鉴完全背包之前的套路

定义为前i种物品中取总重量不超过j的最大价值，则

 

k则是枚举当前物品取的件数。 

与之不同的是由于个数的限制，k有了新的上限： a[i]表示第i件物品的数量

转化为01背包问题

0-1背包是所有背包问题中的老大——鲁迅（我真没说过）

由于上述算法时间复杂度高到飞起，所以我们要优化。

可以把每一件物品拆成一件一件的，用0-1背包做（0-1背包不排斥相同的物品）

（所以我用这个方法骗了许多题）然而这个时间复杂度在数据大的时候还是卡不过呀，比如 51Nod 1086 背包问题 V2 

所以？？？

二进制优化

所以我们要用神奇的二进制 优化

显而易见 ，如果我们把一个数拆分成多个2的幂的和，那么用这些2的幂一定可以凑出1~n的所有的数

这个我们可以从二进制数来理解。

然后，如果我们把一个数分成 1,2,4,8······直到不能再分的时候，还剩一个n 那么用这些书也一定可以凑出1~n的所有的数

但是我不会严谨的数学证明_(:з」∠)_

但是我们可以举个栗子：

eg: 13=1+2+4+6

1=1

2=2

3=1+2

4=4

5=1+4

6=6

7=1+6

8=2+6

9=1+2+6

10=4+6

11=1+4+6

12=2+4+6

13=1+2+4+6

说这么多其实就是要证明：如果我们把m件物品拆成 1,2,4,8······直到不能再分的时候，还剩一个n 件物品  而这些拆分的正确性与拆成一件一件的是一样的（误，正确性一样好像有些奇怪，是都正确的意思啦）

而可以把复杂度降到log级别

还是贴个代码吧 

while(k<=c)
		{
			w[++n]=ww*k;
			p[n]=pp*k;
			c-=k;
			k<<=1;
		}
		if(c>0)
		{
			w[++n]=ww*c;
			p[n]=pp*c;
		}

可行性问题

这个其实我之前还没有想到过，最初是在“背包九讲”上看到的，判断可行性的话我一般比较喜欢直接让dp[j]表示恰好装满j的价值最小，然后判断dp[W]是不是INF

但是人家有比我更快的方法诶

（来源：背包问题九讲）

混合三种背包问题

困难的问题是由简单的问题堆积而来的，前面的三种基本模型都是板儿啊~~~ 博大精深的OI怎么可能只有板儿啊对吧，所以我们要把简单的问题复杂化，把三种背包结合在一起看它们会碰撞出怎样的火花！_(:з」∠)_（好牵强qwq）

其实我觉得混合背包也不难，就是有的物品只有一件，有的物品有无数件，有的物品有有限件

做法吧，还是先把有限件的拆成0-1背包，然后考虑到0-1背包和完全背包就是第二维的枚举顺序不同，就可以用一个for然后判断这件物品是哪种背包里的。

然后就是根据题目要求进行背包，有的题目不止背包物品，比如这个：The Fewest Coins POJ - 3260

---

最后再扯两句

比较基础的几种背包模型就是这里了

思路和部分资料借鉴自“背包九讲”  ，都有标注 博文中其它部分均为原创 转载请说明或留言！

如果博文有什么问题可以 call me at: [email protected]   我会尽量答复

嘢，好像三句了，不对加上这句有四句了，哎呀不管了