美团2017编程题—拼凑钱币&大富翁游戏&最大矩形面积&最长公共连续子串

拼凑钱币

题目描述

给你六种面额 1、5、10、20、50、100 元的纸币，假设每种币值的数量都足够多，编写程序求组成N元（N为0~10000的非负整数）的不同组合的个数。

输入描述:

输入包括一个整数n(1 ≤ n ≤ 10000)

输出描述:

输出一个整数,表示不同的组合方案数

输入例子1:

1

输出例子1:

1

思路

完全背包问题

代码

#include
using namespace std;
#define MAX_N 10001
#define M 6
int main(){
    int n;
    cin >> n;
    int coins[M] = { 1, 5, 10, 20, 50, 100 };   //6种纸币所对应的面值
    long long dp[MAX_N][M]; //dp[i][j]表示用前j+1种纸币组成i元的不同组合个数
    /*for (int j = 0; j < M; j++)
        dp[1][j] = 1;*/
    for (int i = 0; i <= n; i++)//i从0开始，即用1元的组成0元，也有1中组合方案，就是不拿
        dp[i][0] = 1;
    for (int i = 1; i <= n; i++){
        for (int j = 1; j < M; j++){
            dp[i][j] = 0;
            int m = i / coins[j];   //对于第j+1种纸币，面值为coins[j],可以用m张coins[j]组成i元
            for (int k = 0; k <= m; k++){
                dp[i][j] = dp[i][j] + dp[i - k*coins[j]][j - 1];
            }
        }
    }
    cout << dp[n][5];
    system("pause");
    return 0;
}

大富翁游戏

题目描述

大富翁游戏，玩家根据骰子的点数决定走的步数，即骰子点数为1时可以走一步，点数为2时可以走两步，点数为n时可以走n步。求玩家走到第n步（n<=骰子最大点数且是方法的唯一入参）时，总共有多少种投骰子的方法。

输入描述:

输入包括一个整数n,(1 ≤ n ≤ 6)

输出描述:

输出一个整数,表示投骰子的方法

输入例子1:

6

输出例子1:

32

代码

#include
using namespace std;

int main(){
    int n;
    cin >> n;

    int dp[7] = {0};
    dp[1] = 1; dp[2] = 2;
    for(int i =0; i <= n; i++){
        dp[i] = 1;
        for(int j = 1; j < i; j++)
            dp[i] += dp[j];
    }

    cout << dp[n] <"pause");
    return 0;
}

最大矩形面积

题目描述

给定一组非负整数组成的数组h，代表一组柱状图的高度，其中每个柱子的宽度都为1。 在这组柱状图中找到能组成的最大矩形的面积（如图所示）。 入参h为一个整型数组，代表每个柱子的高度，返回面积的值。

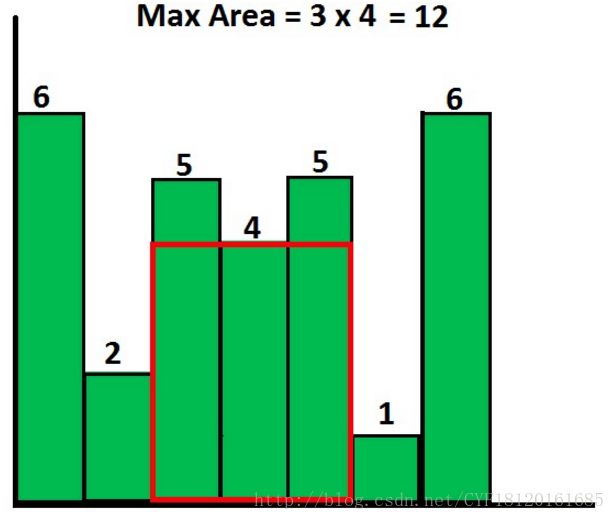
输入描述:

输入包括两行,第一行包含一个整数n(1 ≤ n ≤ 10000)
第二行包括n个整数,表示h数组中的每个值,h_i(1 ≤ h_i ≤ 1,000,000)

输出描述:

输出一个整数,表示最大的矩阵面积。

输入例子1:

6
2 1 5 6 2 3

输出例子1:

10

代码

#include
#include

using namespace std;
int main(){
    int n;
    cin >> n;
    vector<long> h(n+1);
    for (int i = 1; i <= n; i++)
        cin >> h[i];
    vector<vector<long>> dp(n+1, vector<long>(n+1));
    for (int i = 1; i <= n; i++)
        dp[i][i] = h[i];

    int min_h;
    for (int i = n-1; i >= 1; i--){
        for (int j = i; j <= n; j++){
            min_h = h[i];
            for (int k = i; k <= j; k++)
                min_h = min_h < h[k] ? min_h : h[k];
            dp[i][j] = (min_h *(j - i + 1)) > dp[i][j - 1] ? (min_h *(j - i + 1)) : dp[i][j - 1];

            dp[j][i] = dp[i][j] = dp[i][j] > dp[i + 1][j] ? dp[i][j] : dp[i + 1][j];
        }
    }
    cout << dp[1][n] << endl;
    system("pause");
    return 0;
}

最长公共连续子串

题目描述

给出两个字符串（可能包含空格）,找出其中最长的公共连续子串,输出其长度。

输入描述:

输入为两行字符串（可能包含空格），长度均小于等于50.

输出描述:

输出为一个整数，表示最长公共连续子串的长度。

输入例子1:

abcde
abgde

输出例子1:

2

代码

最长公共子序列

#include
#include
#include
using namespace std;

int main(){
    string s1,s2;
    cin >> s1;
    cin >> s2;
    int len1 = s1.length();
    int len2 = s2.length();

    int res = 0;
    vector<vector<int>> dp(len1+1,vector<int>(len2+1));
    //初始化
    for(int i=0; ifor(int j=0; j0;
        }
    }
    for(int i=1; i<=len1; i++){
        for(int j=1; j<=len2; j++){
            if(s1[i-1]==s2[j-1])
                dp[i][j] = dp[i-1][j-1]+1;
            else
                dp[i][j] = dp[i-1][j] > dp[i][j-1] ? dp[i-1][j] : dp[i][j-1];
        }
    }
    cout << dp[len1][len2] << endl;
    system("pause");
    return 0;
}

最长公共连续子序列

#include
#include
#include
using namespace std;

int main(){
    string s1,s2;
    getline(cin, s1);//读取一行字符串（包括空格）
    getline(cin, s2);
    int len1 = s1.length();
    int len2 = s2.length();

    vector<vector<int>> dp(len1+1,vector<int>(len2+1));
    //初始化
    for(int i=0; i<=len1; i++){
        for(int j=0; j<=len2; j++){
            dp[i][j] = 0;
        }
    }
    int res = 0;
    for(int i=1; i<=len1; i++){
        for(int j=1; j<=len2; j++){
            if(s1[i-1]==s2[j-1]){
                dp[i][j] = dp[i-1][j-1]+1;
                res = res > dp[i][j] ? res : dp[i][j];
            }
            else
                dp[i][j] = 0;

        }
    }
    cout << res << endl;
    system("pause");
    return 0;
}