特征离散化系列(一)方法综述

致谢老婆大人为本期博客创作配图，你的支持是我坚持下去的动力

特征离散化系列一方法综述

数值离散化在数据挖掘和发现知识(data mining and knowledge discovery)方面扮演者重要的角色。许多研究表明归纳任务(induction tasks)能从离散化(discretization)中获益：有离散值的规则通常是更简短，更容易理解，并且离散化能改善预测精度(predictive accuracy)。文献中提到的很多归纳算(induction algorithms)法都需要离散特征。所有的这些特点促进研究人员和实践人员(researchers and practitioners)在开展机器学习或者数据挖掘任务之前都要进行连续特征离散化。在文献中能查到很多离散化的方法。本文旨在对离散化方法做一个系统性的研究，追溯它们发展的历史，以及这些方法对分类的影响，速度和精度之间的权衡(trade-off)。本文也给出了不同方法间的对比实验，并对结果进行了分析。本文的贡献主要有：对现存的离散化方法进行概述总结，对现有离散化方法进行归类的层次化结构描述(hierarchical framework)，为进一步发展铺路(pave the way)，对典型的离散化方法(representative discretization methods)的简要讨论，大量的试验和分析，在不同的应用环境下选择离散化方法的原则。同时也发现了一些需要去解决的问题，以及对离散化的进一步研究。

关键词：discretization; continuous feature; data mining; classification

本文内容结构安排如下：

• 1 概述Introduction
• 2 当前状态current status
• 3 离散化过程discretization process
• 4 离散化框架discretization framework
• 5 实验和分析experiments and analysis
• 6 结论和下一步工作conclusion and future work

1.概述Introduction

数据通常以混合的形式出现：nominal，discrete，continuous。离散或者连续型数据属于定序数据类型(ordinal data types)，数据之间有次序，然而对于定类数据类型(nominal data types)，数据之间并不拥有次序。对于连续型属性其取值个数是无限大的，离散属性取值通常是有限的。这两种数据类型在学习分类树/规则时是不一样的。相比于连续属性值，离散属性值有一下优点：①通过离散化数据将被简化并且减少；② 离散特征更容易被理解，使用和解释；③ 离散化使学习更加准确，快速；④使用离散特征获得的结果(decision trees,induction rules)更加紧凑，简短，准确，结果更容易进行检查，比较，使用和重复使用；⑤ 很多分类学习算法只能处理离散数据。离散化是量化(quantizing)连续属性的过程。离散化的成功可以很大程度上扩展(extend the borders)许多学习算法的使用领域。

本文回顾了现存的离散化方法，标准化了离散化过程，以一个简要的框架总结了它们，并且为进一步研究和发展提供了一些方便的参考。本文余下的工作按照如下结构组织。Section 2总结了离散化方法的当前状态；Section 3以统一的词汇(unified vocabulary)讨论了不同的离散化方法，定义了离散化的通用处理过程，考虑了不同的离散化结果评价方法，Section 4提出了新的用于离散化方法的层次框架(hierarchical framework)，简洁的描述了典型的方法。当描述每一个典型的方法时，我们基于基准数据集(benchmark data set)Iris给出了离散化结果。该数据集是一个小型数据集，通常用于离散化和分类工作，在这里使用是为了说明不同的算法的工作过程。Section 5比较了不同方法的实验结果，并对结果进行了分析。Section 6给出了选择离散化方法的直到准则和下一步工作。

2.当前状态current status

早期，诸如等宽(equal-width)，等频(equal-frequency)等技术用于离散化。伴随着精确度的需求以及有效的分类算法的发展，离散化的技术得到了快速发展。过去几年间，提出了许多离散化技术。试验表明离散化在减小数据大小、甚至改善预测精度方面都有着很大的潜力。离散化方法朝着不同的主线发展来满足不同的需求：监督与无监督(supervised vs, unsupervised)；动态与静态(dynamic vs. static)；全局与局部(global vs. local)；自顶向下与自底向上(splitting(top-down) vs. merging(bottom-up))；直接与增量(direct vs. incremental)。

监督与无监督(supervised vs, unsupervised)：离散化是监督或者无监督，取决于离散化过程中离散化方法是否使用了分类信息。监督离散化使用了分类信息去指导离散化过程；然而无监督离散化却没有。没有分类信息的离散化方法类似于早期的等宽(equal-width)，等频(equal-frequency)技术：根据用户预先指定的宽度(range of values)或者频率(number of instances in each interval)将连续的范围(continuous ranges)划分成各个子范围(subranges)。

对于连续属性值的分布不是均匀分布时，这可能不会给出好的结果。因此它对于异常值(outliers)是弱小的(vulnerale)，因为他们明显影响了取值范围。为了克服这个缺点，引入了监督离散化方法，分类信息用于找到合适的用分割点(cut-points)定义的间隔(intervals)。已经设计(devised)了不同的使用分类信息的方法去在连续属性上寻找有意义的间隔。如果没有分类信息可以利用，无监督离散化方法是唯一选择。没有太多的无监督离散化方法在文献中提到，可能归因于(attribute to)离散化通常与分类任务有关。

动态与静态(dynamic vs. static)：离散化方法的应用可能是动态的，也有可能是静态的。所谓动态方法就是指离散化连续值是在分类器正在被建立的时候，诸如C4.5，静态离散化先于分类任务完成。[文献][9]对动态和静态方法做了比较。作者也报道了当测试C4.5时使用和不使用离散化特征时的混合性能。

全局与局部(global vs. local)：另一个分法(dichotomy)是全局与局部。局部离散化方法是在实例空间(instance space/subset of instances)的局部区域(localized region)进行的离散化。然而全局离散化使用了全体实例空间进行离散化。当实例空间的一个区域被用来离散化时局部方法通常与动态离散化方法有关。

自顶向下与自底向上(splitting(top-down) vs. merging(bottom-up))：离散化方法也可以根据自顶向下与自底向上进行划分。自顶向下方法以一个空的分割点(cut-points/split-points)列表开始，在离散化进程中一直不断的往这个列表中通过splitting intervals添加新的分割点。自底向上以完整的列表开始，该列表用所有的连续特征值作为分割点，在离散化进程中一直不断的给这个列表中通过merging intervals移除的分割点。

直接与增量(direct vs. incremental)：直接方法同时划分K个间隔的范围(例如equal-width，equal-frequency，K-means)，需要一个额外的输入来决定间隔的个数。增量方法以一个简单的离散化开始，并伴随着改善或者提纯(refinement)过程，需要停止准则来终止下一步的离散化。

综上所述，有许多离散化方法，并以不同的维度对它们进行分组。有时对用户而言对于手头的数据很难找到一个合适的方法。[文献][9,4]给出了几种减轻这种困难的方法。我们继续对这些关键问题进行全面的研究，包括：离散化过程的定义(definition of a discretization process)，性能度量(performance measure)，广泛的对比(extensive comparison)。

本文的贡献主要有：
1) 典型的离散化过程的简要描述；
2) 新的层次化框架去分类文献中提到的现存的离散化方法；
3) 对不同的离散化方法使用基准数据集对其结果进行系统论述；
4) 对从这个框架下沿着基于公开数据集的分类学习算法的时间消耗和错误率这两个维度选出的9个代表性的离散化方法进行对比；
5) 对对比结果进行详细检查；
6) 对不同的使用环境选用何种方法给出指导准则，给出下一步研究的方向；

3.离散化过程discretization process

首先我们阐明(clarify)几个术语(terms)，以对典型的离散化过程进行简要描述。

3.1术语和符号terms and notations

特征feature
特征(feature)，属性(attribute)，变量(variable)是数据的一方面。通常在收集数据之前，特征应该被指定或选择。特征可能是离散的、连续的、定类的。本文我们的兴趣主要在离散连续特征的过程。接下来用M表示数据集中特征的个数。

实例instance
实例(instance)、元组(tuple)、记录(recor)、数据点(data point)是一次数据记录所有特征的特征值。实例的集合产生数据集。通常数据集每行代表一个实例，每列代表一个特征。用N表示数据中实例的个数。

分割点cut-point
术语分割点(cut-point)指的是连续值范围中的一个实数值，它将这个范围分割成两个间隔。一个间隔是小于等于这个分割点的，另一个是大于分割点的。例如，一个连续的间隔[a,b]被分割成[a,c]和[c,b]，值c就是分割点。分割点(cut-point)也被叫做分离点(split-point)。

元数arity
术语元数(arity)在离散化环境中就是间隔或者划分的个数。在离散化连续特征之前，元数被设置成k-连续特征的划分数。最大的分割点数是k-1。离散化过程减小了元数，但是在元数和分类或其他任务的性能之间做了折中。元数太大，会使学习过程变得更长，但是元数太小，会影响预测的精度。

3.2典型离散化过程a typical discretization process

使用“典型”，指的是单变量离散化。离散化可能是单变量的，也可能是多变量的。单变量离散化(univariate discretization)一次只离散化一个连续特征，然而多变量离散化(multivariate discretization)同时考虑多个特征。本文主要考虑了单变量离散化，文章末尾简单讨论了多变量离散化，作为单变量离散化的扩展。
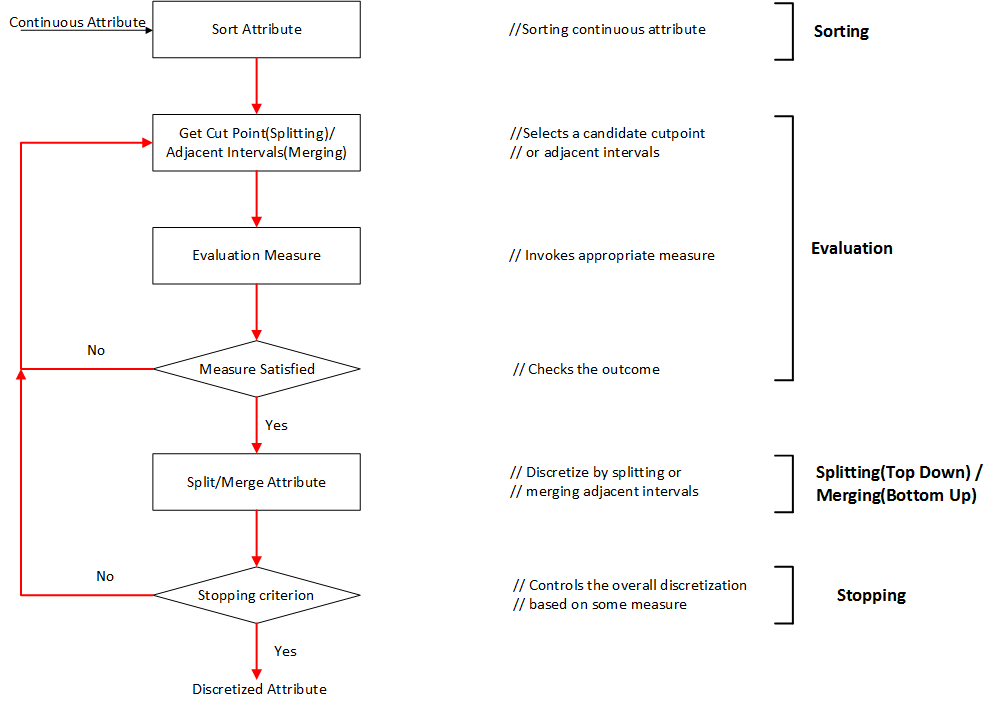
典型的离散化过程通常由以下4步组成：
1) sort对离散化的特征的连续值进行排序；
2) evaluate对为了合并的划分的或者邻近的间隔，评估分割点；
3) split or merge通过一些准则，划分或者合并连续值的间隔；
4) stop停止离散化。

排序sorting
对特征的连续值进行降序或者升序排序都可以。如果不关心在离散化时进行排序，那么排序的计算代价将是非常昂贵的。对于所有的特征，排序在离散化开始之前完成，这将是一个全局处理(global treatment)，适用于将整个实例空间离散化。如果排序在过程的每一次迭代时完成，这将是一个局部处理(local treatment)，仅对整个实例空间的一个区域进行离散化。

选择分割点 choosing a cut-point
排序之后，离散化过程接下来的一步是寻找最好的分割点，对连续值的范围进行划分，或者寻找最好的一对邻近的间隔进行合并。一个典型的评价函数用来决定一次划分或者合并与类别标签的关系。文献中提到很多评价函数，诸如：熵测量、统计测量。关于评价函数与它们的应用将在下一小节进行讨论。

划分/合并Splitting/merging
正如我们所知，对已自顶向下的方法，间隔是划分；然而对于自底向上的方法，间隔是合并。对于划分，需要评价分割点，选择最好的一个，并将连续值范围划分成两部分。分别对每一部分进行离散化直到满足停止准则。对于合并，评估邻近的间隔，找到最好的间隔进行合并。离散过程一直持续，间隔数随之减少，直到满足停止准则。

停止准则stopping criteria
停止准则是为了终止离散过程。它经常被元数和精度的折中所支配，因为这两个是正互相关的(positively correlated)。我们可以将k作为离散化的结果的元数设置一个上界，事实上，上界k的设置是远小于N的，假设没有特征连续值的副本，停止准则可能是非常简单的，诸如在一开始固定间隔数，或者一个稍微复杂一些的如评价函数。在下一章节描述不同的停止准则。

3.3离散化方法对比comparison of discretization methods

针对不同离散化方法获得的离散化数据，哪一个更好呢？看起来是一个简单的问题，却很难用简单的答案来回答。这是因为不同的方法之间的比较是一个复杂的问题，它依赖于用户在某一个特殊应用的需求。说复杂是因为不同方法的评价可以从多个方面来进行。我们列举了3个重要的维度：(1)总的间隔数，直观的，间隔点越少，离散化结果越好；但是强加于数据呈现是有限的。这导致第二个维度。(2)离散化引起的不一致性的个数。它不应该大于离散化之前原始数据的不一致数。如果最终结果是从数据训练一个分类器，应该考虑另一个观点。(3)预测精度-离散化对预测精度的改善。简言之，我们至少需要三个维度的考虑：简化(simplicity)、一致性(consistency)、精度(accuracy)。理想情况下，最好的离散化结果在这三方面应都有最高的得分。但事实上，它是不可能达到的，或者不需要的。为不同的离散化方法在这三方面提供一个均衡的观点也是本文的目标。

简化(simplicity)使用分割点的总数来定义的。精确度(accuracy)在交叉验证模式下运行分类器可以获得。一致性(consistency)是最小的不一致性计数值，可以通过以下3步计算而来(下面的描述中，模式pattern指没有类别标签的实例)：(1)如果两个实例有着相同的属性值，但是类别标签不一样，则这两个实例是不一致的；例如，如果两个实例是(0 1;0)和(0 1;1)，它们就是不一致的。(2)一个模式的计数值是这个模式出现在数据中的次数减去最大的类别标签数；例如，假设有n个实例与这个模式相匹配，其中label1的个数是c1, label2的个数是c2，label3的个数是c3，其中c1+c2+c3=n。如果c3是这三个中最大的，则该模式的不一致性计数值为(n-c3)。(3)总的不一致性计数是一个特征集合中所有可能的模式的不一致性计数值之和。

4.离散化框架discretization framework

文献中提到很多离散化方法。正如上面所述的一样，根据不同的维度可以对这些方法进行分类。即：监督与无监督(supervised vs, unsupervised)；动态与静态(dynamic vs. static)；全局与局部(global vs. local)；自顶向下与自底向上(splitting(top-down) vs. merging(bottom-up))；直接与增量(direct vs. incremental)。可以根据这些维度的不同组合来对这些方法进行分组。我们希望构建一个系统的、可扩展的、能覆盖现在所有方法的框架。文献中提到的每一种离散化方法离散化一个特征：或者对连续值划分间隔；或者合并邻近的间隔。划分和合并根据是否使用分类信息可进一步分组成监督与无监督。
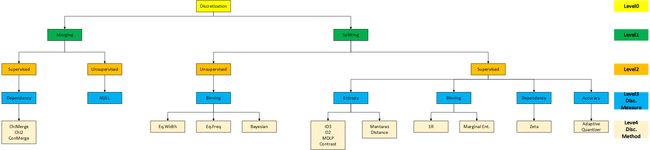
鉴于这些方面的考虑，我们提出了层次化框架(hierarchical framework)，如下图所示。

通过两种方法：划分和合并，描述了不同的离散化测量(level1)。接着我们考虑了方式是监督还是无监督(level2)。进一步我们将使用相同离散化度量方法的分组在一起(level3)，例如分箱(binning)和熵(entropy)。如下图所示，监督与无监督划分决定了不同的度量方法。因此概念上有用的划分将不再详细讲述。

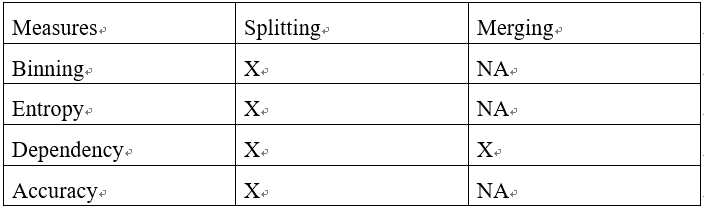
我们将讨论如下表所示的基于划分和合并的分类方法的现存的不同的度量方式。

在以下两个小节，将选择典型的方法进行深入讨论(in-deep discussion)。它们相关的或者派生的(related or derived)度量方法也会简要涉及。对每一个离散化度量方式，我们主要给出：
(1). 度量方式的定义；
(2). 在离散化方法中的应用；
(3). 使用的停止准则；
(4). 对Iris数据集的离散化结果：每一个属性的分割点；
在小节的最后，出于对比目的，我们给出了所有离散化度量方式的结果列表：不一致性的个数、离散化的分割点。

4.1划分方法splitting method

我们以用于划分离散化方法的通用算法开始。

在离散化过程中划分算法(splitting algorithm)由4步组成，它们是：
(1). 对特征值排序；
(2). 搜索合适的分割点；
(3). 根据分割点划分连续值的范围；
(4). 当满足停止准则的时候停止离散化否则继续；
文献中提到很多划分离散化度量方法：分箱(binning)、熵(entropy)、独立性(dependency)、精确度(accuracy)。

注：这些方法我们将开设独立的博客去说明讨论。

分箱binning

• Equal width or frequency
• 1R

熵entropy

• ID3 type
• D2
• Ent-MDLP
• Mantaras distance

独立性dependency

• Zeta

精确度accuracy

• adaptive quantizer

4.2合并方法merging method

我们以采用合并或者自底向上方法的离散化通用算法开始。

在离散化过程中合并算法由4个重要步骤组成，它们是：
(1). 对值进行排序；
(2). 找到最好的两个相邻间隔；
(3). 把这一对合并成一个间隔；
(4). 满足停止条件时终止。

注：这些方法我们将开设独立的博客去说明讨论。

chi-square measure

ChiMerge

chi2

4.3讨论discussion

我们已经回顾了在划分和合并归类情况下的典型离散化方法。大部分方法是基于划分方法的。我们使用Iris数据集作为一个例子展示了不同的离散化方法的结果。两种度量方式(number of inconsistencies and number of cut-points)直觉上的关系是：分割点越多，不一致计数越少。仔细观察表明(closer look)让两个计数值都少可能有一个妥协(middle ground)的方法。因此，我们应该旨在去让两个数值(number of inconsistencies and number of cut-points)都小。我们确实发现对于Iris数据一些方法比其他方法要好：Ent-MDLP是划分方法里边最好的；chi2是合并方法里边最好的。Chi2也表明，通过考虑一定程度的不一致性，在两种度量方式之间达到折中也是可能的。除离散化之外(in addition to)，Chi2也移除了具有一定程度的不一致性的特征。

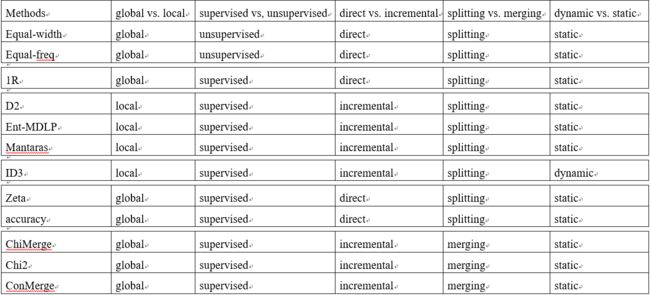
在section2，我们通过5种不同的维度回顾了监督与无监督(supervised vs, unsupervised)；动态与静态(dynamic vs. static)；全局与局部(global vs. local)；自顶向下与自底向上(splitting(top-down) vs. merging(bottom-up))；直接与增量(direct vs. incremental)的离散化方法。在多维观点(muti-dimensional view)下我们又得到了另外一种类型的分组。如下表所示：

本期博客主要对特征离散化方法进行了综述，下期博客将对具体离散化方法及其方法试验展开说明。

博客预告：近期本人将推出卷积神经网络之父Yann LeCun的Energy-Based Model，以及基于该模型的协同人脸检测与姿态估计算法以及试验实现。欢迎大家关注。