Word Embedding

同样是在上一篇博客中我所提到的最近在看的论文使用的模型中，初次接触Word Embedding。就是下面这个模型（Figure 3），让我一个小白被迫的主动学习了超多基础知识，当然，我在拿着这篇论文去给老师讲的时候脑子并没有缕的很清楚，现在想想，真是辛苦老师了。

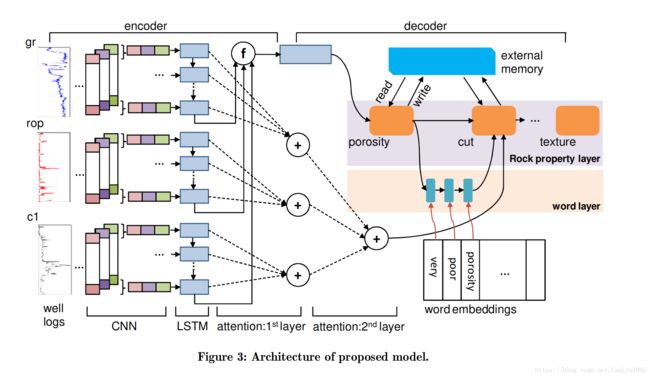
话不多说，进入正题，说说我对Word Embedding的理解。文章内容借鉴吴恩达的视频和大牛YJango的专栏。

单词表达

在卷积神经网络中，图像在计算机中是一堆按顺序排列的数字，数值为0到255。0表示最暗，255表示最亮。 你可以把这堆数字用一个长长的向量来表示，也就是tensorflow的mnist教程中784维向量的表示方式。 然而这样会失去平面结构的信息，为保留该结构信息，通常选择矩阵的表示方式。同样，单词也需要用计算机可以理解的方式表达后，才可以进行下一步的操作。

One hot representation

程序中编码单词的一个方法就是one hot representation，要理解这种表达方式我们首先得知道vocabulary（词汇表）。

• 实例
  如果我们有一个由1000个单词组成得词汇表，表示为：
  [a，an，and，…，people，…，person，…，relu]
  在这么一张词汇表中，a是第1个单词，abbreviations为第2个单词，zoology为第999个单词，zoom为最后一个单词。那么以上四个单词可以表示为一个只有一个位置为1其余位置为0的1000维的向量（one-hot向量）。如下图所示。
  

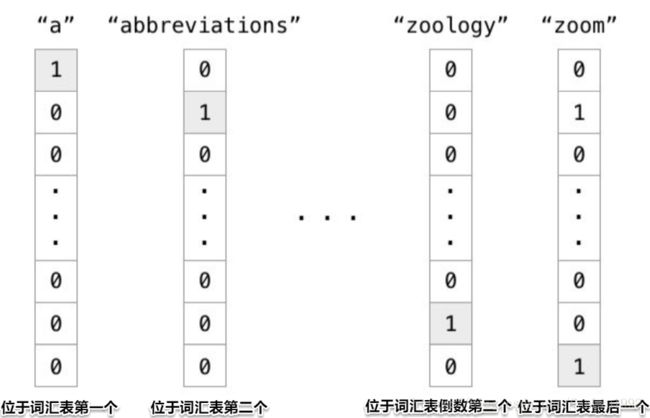
  也就是说，在one hot representation编码的每个单词都是一个维度，彼此independent。

Featurized representation

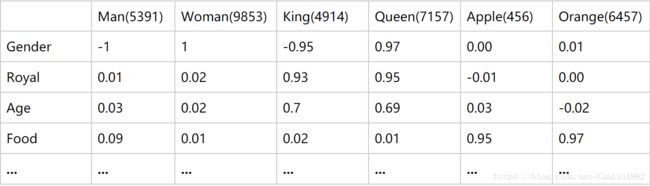
在上述表示方法中，每个单词都是相互独立的向量，他们的内积一直都为0。所以，这种表示方式并不能很好的表示数据之间的关联性。然而，在现实生活中，我们知道大量的单词都是彼此相关的。

• 语义：girl和woman虽然表述不同年龄段的女性，但性别是一样的。
• 复数：word和words仅仅是单复数的区别。
• 时态：buy和bought表达的都是“买”，但发生的时间不同。
  而使用one-hot representation的编码方式，无法体现上述特征关联性。我们更希望用诸如语义”，“复数”，“时态”等维度去描述一个单词。每一个维度不再是0或1，而是连续的实数，表示不同的程度。

举例如下图，将上述几个单词用高维特征表示：

Word Embedding

何为Embedding?

Embedding可以看作是数学上的一个空间映射(Mapping)：map( lambda y: f(x) )，该映射的特点是：单射、映射前后结构不变，对应到word embedding概念中可以理解为寻找一个函数或映射，生成新的空间上的表达，把单词one-hot所表达的X空间信息映射到Y的多维空间向量。

目的

所以，我们到底为什么想要用Featurized representation的方式去表达一个单词呢？下面从两个角度说明。

数据量角度

这需要再次记住我们的目的：
从大量的样本$\{(x_i,y_i{)}_{i=1}^N\}$ 中，寻找可以较好预测未见过 $x_{new}$所对应 $y_{new}$ 的函数 $f:x\to y$。

实例: 上面的概念很好理解，比如在我们日常生活的学习中，大量的 $\{(x_i,y_i{)}_{i=1}^N\}$就是历年真题， $x_i$ 是题目，而 $y_i$ 是对应的正确答案。高考时将会遇到的 $x_{new}$ 往往是我们没见过的题目，希望可以通过做题训练出来的解题方法 $f:x\to y$ 来求解出正确的 $y_{new}$ 。

如果可以见到所有的情况，那么只需要记住所有的 $x_i$ 所对应的 $y_i$ 就可以完美预测。但正如高考无法见到所有类型的题一样，我们无法见到所有的情况。这意味着：
机器学习需要从有限的例子中寻找到合理的 f 。

高考有两个方向提高分数：
（1）：训练更多的数据：题海战术。
（2）：加入先验知识：尽可能排除不必要的可能性。
问题的关键在于 训练所需要的数据量 上。

同理，如果我们用One hot representation去学习，那么每一个单词我们都需要实例数据去训练，即便我们知道"Cat"和"Kitty"很多情况下可以被理解成一个意思。

词嵌入的一个显著成果就是可学习的类比关系的一般性。

神经网络分析

假设我们的词汇只有4个，girl, woman, boy, man，下面就思考用两种不同的表达方式会有什么区别。

One hot representation

尽管我们知道他们彼此的关系，但是计算机并不知道。在神经网络的输入层中，每个单词都会被看作一个节点。 而我们知道训练神经网络就是要学习每个连接线的权重。如果只看第一层的权重，下面的情况需要确定4*3个连接线的关系，因为每个维度都彼此独立，girl的数据不会对其他单词的训练产生任何帮助，训练所需要的数据量，基本就固定在那里了。

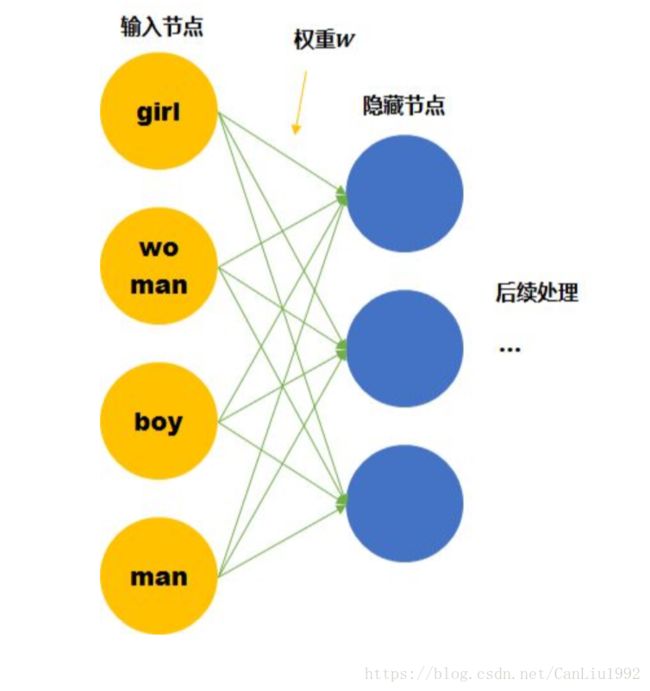
Featurized representation

我们这里手动的寻找这四个单词之间的关系 $f$ 。可以用两个节点去表示四个单词。每个节点取不同值时的意义如下表。 那么girl就可以被编码成向量[0,1]，man可以被编码成[1,1]（第一个维度是gender，第二个维度是age）。

那么这时再来看神经网络需要学习的连接线的权重就缩小到了2*3。同时，当送入girl为输入的训练数据时，因为它是由两个节点编码的。那么与girl共享相同连接的其他输入例子也可以被训练到（如可以帮助到与其共享female的woman，和child的boy的训练）。

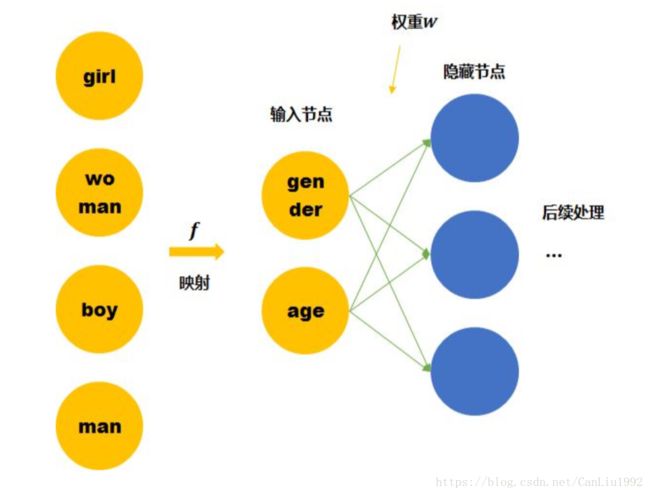
Word embedding也就是要达到第二个神经网络所表示的结果，降低训练所需要的数据量。

而上面的四个单词可以被拆成2个节点的是由我们人工提供的先验知识将原始的输入空间经过 $f$ (上图中的黄色箭头)投射到了另一个空间（维度更小），所以才能够降低训练所需要的数据量。 但是我们没有办法一直人工提供，机器学习的宗旨就是让机器代替人力去发现pattern。

Word embedding就是要从数据中自动学习到输入空间到Featurized representation空间的映射$f$ 。

训练方法

问题来了，我们该如何自动寻找到类似上面的关系，将One hot representation转变成Featurized representation。 我们事先并不明确目标是什么，所以这是一个无监督学习任务。

无监督学习中常用思想是：当得到数据$\{(x_i,y_i{)}_{i=1}^N\}$后，我们又不知道目标（输出）时，

• 方向一：从各个输入 ${x_i}_{i=1}^N$之间的关系找目标。 如聚类。
• 方向二：并接上以目标输出 $y_i$ 作为新输入的另一个任务 $g:y\to z$ ，同时我们知道的对应 $z_i$ 值。用数据 $\{(x_i,z_i{)}_{i=1}^N\}$ 训练得到 $k:x\to z$ ,也就是 $z=g(f(x))$ ，中间的表达 $y=f(x)$ 则是我们真正想要的目标。如生成对抗网络。

Word embedding更偏向于方向二。 同样是学习一个 $k:x\to z$ ，但训练后并不使用 $k$ ，而是只取前半部分的 $f:x\to y$ 。

到这里，我们希望所寻找的 $k:x\to z$ 既有标签 $z$ ，又可以让 $f(x)$ 所转换得到的 $y$ 的表达具有Featurized representation中所演示的特点。

同时我们还知道，单词意思需要放在特定的上下文中去理解。 那么具有相同上下文的单词，往往是有联系的。

实例：

• 这个可爱的 泰迪 舔了我的脸。
• 这个可爱的 金巴 舔了我的脸。

从上面这个例子我们可以找到一个 $k:x\to z$ ：预测上下文。用输入单词 $x$ 作为中心单词去预测其他单词 $z$ 出现在其周边的可能性。

我们既知道对应的 $z$ ，同时该任务 $k$ 又可以让 $f(x)$ 所转换得到的 $y$ 的表达具有Featurized representation中所演示的特点。 因为我们让相似的单词（如泰迪和金巴）得到相同的输出（上下文），那么神经网络就会将 泰迪的输入 和 金巴的输入 经过神经网络 $f(x)$ 得到的 泰迪的输出 和 金巴的输出 几乎相同。

用输入单词作为中心单词去预测周边单词的方式叫做：Word2Vec The Skip-Gram Model。
用输入单词作为周边单词去预测中心单词的方式叫做：Continuous Bag of Words (CBOW)。