用A*、IDS(深度迭代算法)、贪心算法解决八数码
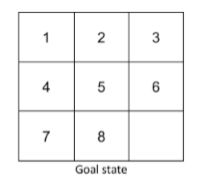
八数码问题——给定随机生成的初始状态和如下的目标状态,分别实现 IDS (迭代深度搜索)、贪婪搜索以及A*搜索算法,找到一个从初始状态到目标状态的行动路径。
要求:
- A*算法至少需要实现 2种启发式函数
- 根据结果对比分析不同搜索算法的运行时间,注意返里的运行时间取多次不同随机初始状态的运行时间的平均结果。
先大概说一下这三种方法的思路:
- A*搜索:总代价 f(n) = g(n) + h(n),其中g(n)为从初始状态到达该状态的代价(这里一个状态也就是A*算法里常说的一个节点),h(n)为从当前状态到目标状态的预估代价。因此,该算法的思路就是,每次寻找总代价f(n)最小的点进行扩展,直到找到终点。A* 的具体过程可参考这篇博客,我就是看这篇博客看会的A* :https://blog.csdn.net/hitwhylz/article/details/23089415
- 贪心搜索:代价f(n) = h(n),每次只考虑(可到达的)离目标节点最近的点进行扩展
- IDS深度迭代搜索:在有界的深度优先搜索的基础上迭代的设置边界,即先考虑一层的DFS,若找不到目标则找两层的DFS,一直迭代下去直到找到目标节点。所以这种方法也是一定能找到界的,只是时间消耗会很多。
有人说,A*是的代价函数是考虑了g和h,贪心的代价是只考虑了h,那么只考虑g的是什么算法呢? 答案就是我们数据结构中学过的Dijkstra最短路算法。
- Dilkstra算法只考虑当点代价最小的点(f = g),所以需要扩展的节点是最多的,耗时是最长的,但是这种方法一定能找到最优解(也即是路径最短的解);
- 而贪心每次只考虑离目标节点最近的点(f = h),所以很容易很快就能找到目标节点,但是这种方法找到的解往往不是最优的(也就是找到的路径往往不是最短的);
- 那么,A*就是结合了二者的优点 (f = g + h),既考虑当前的代价,有考虑离目标点的预估代价,既保证了找到的解是最优的,又使得所搜速度相对于Dijkstra变快了,因此,A*算法是这几种方法中效率最高的完备(能找到最优解)的方法。
下面简单介绍一下代码思路:
A*算法
- 先生成随机排列的整数0~8
可以用C++的STL库函数random_suffle(temp.begin(), temp.end(),myrandom)来实现,第一第二个参数分别为vector的头迭代器和尾迭代器,然后第三个参数是自己定义的随机函数,这里设置随机数种子srand((int)time(0))便可以使每次生成的序列不一样。
// 随即生成函数
int myrandom (int i) {
return rand()%i;
}
//生成0~8的随机整数序列,作为开始状态
void randperm()
{
vector temp;
for (int i = 0; i < 9; ++i) temp.push_back(i+'0'); //生成0~8
random_shuffle(temp.begin(), temp.end(),myrandom); //随机乱序
for(int i=0;i<3;i++){
for(int j=0;j<3;j++){
start.matrix[i][j] = temp[i*3+j];
}
}
}
- 检查生成的随机序列是否有解
我们知道,若两个不同的状态序列的逆序数同奇偶,则二状态可以互达,否则不能互达。逆序数就是对于每个数,前面比它大的数的个数的总和。我们的目标状态是123456780,那么它的逆序数是0(忽略0板块),是偶排列,那么我们可以计算初始状态的逆序数,如果是偶数,则问题可解;否则问题无解,从初始状态无论怎么移动都无法达到目标状态。
//判断是否有解
//初始状态的逆序数应与目标状态的同奇偶,目标状态为偶排列
bool check_if_solvable()
{
string start_seq = matrix2string(start.matrix);
int cnt=0;
for(int i=0;i<9;i++){
if(start_seq[i]=='0') continue;
for(int j=i-1;j>=0;j--){
if(start_seq[j]>start_seq[i]) cnt++;
}
}
if(cnt%2==0) return true;
return false;
}
- 若问题有解,那么迕入 A*算法
因为要进行多次重复实验,因此每次进入函数时应先将各个变量、各个容器清零,避免上次运行的结果对后面造成影响。同时,初始化初始节点,将初始节点放入open list中。
int AStar(State& start){
//清零
while(!openList.empty()) openList.pop();
openSeq.clear();
closeSeq.clear();
//给start节点的zero_x,zero_y赋值
find_blankTile();
start.g=0;
openList.push(start);
openSeq.insert(matrix2string(start.matrix));
然后遍历open list,每次都取f值最小的出来,因为是优先队列,所以取队首就好了。取出来先判断是否达到目标状态,若达到,则反向搜寻将路径记录下来并返回移动步数;
//遍历,直到open列表为空
while(!openList.empty()){
State *curState = new State(openList.top()); //当前状态。 因为是优先队列, 所以top出来的是f值最小的
//cout<<"round: "<matrix);
//cout<<"parent"<parent<matrix)==matrix2string(goal.matrix)){
int step = curState->g;
/***
根据父节点一步步往回寻路,输出路径
*/
while(!stack_path.empty()) stack_path.pop(); //清空栈
State* p = curState;
while(p!=NULL){
stack_path.push(*p);
p = p->parent;
}
//返回所需步数
return step;
}
否则,沿当前节点(当前状态curState)扩展。因为每个节点(状态)是用结构体表示的,数字排列用二维数组存储,难以直接比较两个状态是否相同,因此这里我将二维数组转成字符串来对比两个序列是否一样,将每个访问过的节点的字符串序列存入到STL set中(即close list),便可以直接用find()函数查找改状态是否在close list中了。
这里代码的思路是这样的:首先将当前节点从openlist中移除并加入到close list中,代表该节点已访问过;然后将该节点向四个方向扩展,若某方向超出范围则跳过,若某方向的状态已访问过(即在close list中)也跳过,那么对于可扩展的点,将父节点设为curState、g值为curState.g加上这一步的代价(这里每一步的代价都为1),然后算得启发式函数值,也就是预估一下从该扩展节点到目标节点的代价,然后将当前代价g加上估算代价得到代价f,并将节点存入open list中。这里我没有判断该扩展节点是否已在开放列表中,按理说A*算法是需要判断的,若节点在开放列表的话,就需要判断这条路径(即从当前节点到达该扩展节点)的代价是否比它原来的代价小,这里只用比较g值就行了,因为同一点到目标节点的估算代价h用同一个启发式函数计算出来是一样的。因为优先队列无法进行查找和更新,且对于这个问题每一步的代价g都是只加1的,因此这里不判断也不会出现问题。
string nextSeq="";//下一个状态的字符串序列
for(int i=0;i<4;i++){ //四个交换方向,分别为上右下左
// cout<<"i: "<zero_x = curState->zero_x+move_x[i];
nextState->zero_y = curState->zero_y+move_y[i];
if(nextState->zero_x<0||nextState->zero_x>2||nextState->zero_y<0||nextState->zero_y>2) continue; //移动超出范围,跳过
nextState->matrix[nextState->zero_x][nextState->zero_y] = '0';//curState->matrix[curState->zero_x][curState->zero_y]; //0
nextState->matrix[curState->zero_x][curState->zero_y] = curState->matrix[nextState->zero_x][nextState->zero_y];
nextSeq = matrix2string(nextState->matrix);
if(closeSeq.find(nextSeq) != closeSeq.end()) continue; //在close列表中,跳过
nextState->g += 1;
nextState->h = cal_h2(*nextState);
nextState->f = nextState->g + nextState->h; //A*算法
//nextState->f = nextState->h; //贪心算法
//nextState->f = nextState->g; //Dijkstra算法
nextState->parent = curState;
openList.push(*nextState);
下面来介绍一下代码中用到的两种启发式函数。第一种是计算有多少个不在正确位置上的数码的个数来作为当前节点和目标节点的相似性度量;第二种是为每个错误放置的数码,计算其到正确位置的城市距离(Manhatton距离),由这些距离之和作为相似性度量,也就是估算代价h。
在设计评估函数时,需要注意一个很重要的性质:评估函数的值一定要小于等于实际当前状态到目标状态的代价。否则虽然程序运行速度加快,但是可能在搜索过程中漏掉了最优解。相对的,只要评估函数的值小于等于实际当前状态到目标状态的代价,就一定能找到最优解。
两种评估函数代码如下:
//启发式函数 h, 不在正确位置的格子的数目
int cal_h(State stat){
int cnt = 0; //记录当前状态跟目标状态瓦片错位的个数
for(int i=0;i<3;i++){
for(int j=0;j<3;j++){
if(stat.matrix[i][j] != goal.matrix[i][j]) cnt++;
}
}
return cnt;
}
//另一种启发式函数 h2,格子横向或竖向走到正确位置的步数,即曼哈顿距离
int cal_h2(State stat){
int manhatton = 0;
bool flag=true;
for(int i=0;i<3;i++){
for(int j=0;j<3;j++){
if(stat.matrix[i][j]==goal.matrix[i][j]) continue;
flag=true; //在goal.matrix找到当前格子就可以退出来了
for(int p=0;flag && p<3;p++){
for(int q=0;q<3;q++){
if(stat.matrix[i][j]==goal.matrix[p][q]){
manhatton += (abs(p-i)+abs(q-j));
flag=false;
break;
}
}
}
}
}
return manhatton;
}
贪心搜索
贪心搜索也是启发式搜索,相比于A*,它每次只找离目标节点最近的节点进行扩展,而不考虑当前的代价,因此实现这个算法只用在A* 的基础上将f=g+h改成f=h即可。代码思路这里就不再重复贴上来了。
迭代深度搜索(IDS,iterative deepening search)
迭代深度索搜其实是深搜(DFS)的一个优化版,普通深搜是一直往下扩展,这样可能会陷入无限循环,IDS是有界的深度搜索,当搜索到一定深度的时候若还没找到解就不再往纵向搜索了,转而向横向搜索。这样,可以先设深度为1,然后迭代的递增深度,若在当前深度搜不到解就继续迭代下一个深度,这样如果问题是有解的,那么总能找到解,且是最优解。因为这种思想类似于广搜,一层一层的迭代,最优解总在较浅层找到。
下面介绍代码。随机序列生成方式以及节点表示等和上面一样,这里不再赘述。这里只介绍IDS算法的实现。
因为深度搜索是FILO(先进后出)的,这里用stack数据结构来维持一个列表。首先将初始节点和节点深度(初始节点深度为0)配成pair入队(栈)。然后遍历这个栈,将栈顶出栈,先判断一下是否达目标状态,没达到的话若深度还没达到最大深度,则扩展,这里注意不能扩展回上前节点的上一个状态,不然就相当于从这个状态来又移回到这个状态去了。将可扩展的节点入栈,这样下次出栈的时候操作的就是这次最后入栈的节点,这也就是深搜的思想。只不过有界的深搜索相当于搜到界限那里就完成了该分支。若全部搜索完都找不到解则返回-1,此时再迭代下一个深度,重复前面的过程,因此这个算法就叫做迭代深度索搜。若状态有解,则IDS一定能找到解,因为深度是可迭代加深的,且是最优解,因为在浅层先找到的解代价最小。 下面是代码:
int IDS(int max_depth){
//初始化start节点
find_blankTile(); start.g=0; start.parent=NULL;
int depth=0; //深度
que.push(make_pair(start,depth)); //将<节点,深度>对 入栈
int curDepth,nextDepth; //当前节点深度,扩展节点深度
node_num=0; //记录总扩展节点数
while(!que.empty()){
node_num++;
State *curState = new State(que.top().first);
curDepth = que.top().second;
que.pop();
if(matrix2string(curState->matrix)==matrix2string(goal.matrix)){
int step = curState->g;
// 据父节点一步步往回寻路,存入stack_path中
// while(!stack_path.empty()) stack_path.pop(); //清空栈
// State* p = curState;
// while(p!=NULL){
// stack_path.push(*p);
// p = p->parent;
// }
return step;//返回所需步数
}
nextDepth = curDepth + 1;
if(nextDepth > max_depth) continue;
string curSeq = matrix2string(curState->matrix); //当前状态的字符串序列
for(int i=0;i<4;i++){
State* nextState = new State(*curState);//下一个状态.先拷贝父节点,之后再改
nextState->zero_x = curState->zero_x+move_x[i];
nextState->zero_y = curState->zero_y+move_y[i];
if(nextState->zero_x<0||nextState->zero_x>2
||nextState->zero_y<0||nextState->zero_y>2) continue; //移动超出范围,跳过
nextState->matrix[nextState->zero_x][nextState->zero_y] = '0';
nextState->matrix[curState->zero_x][curState->zero_y]
= curState->matrix[nextState->zero_x][nextState->zero_y];
//防止移回上一个状态
if(curState->parent!=NULL){ //排除初始节点,因为起始节点没有父节点
if(matrix2string(nextState->matrix)==matrix2string(curState->parent->matrix))
continue; //下个状态的字符串不能跟上个状态一样
}
nextState->g += 1;
//nextState->parent = curState;
que.push(make_pair(*nextState,nextDepth));
}
}
return -1; //找不到解,返回-1
}
运行结果与分析
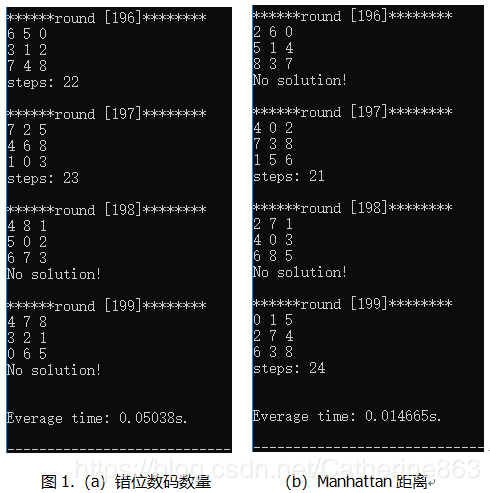
A*的两种评估函数效果对比:
本次实验我跑了200个随机生成的测试样例,然后算出程序平均运行时间,来做效果对比。图中显示的数码版是随机生成的初始序列。可以先来验证一下判断程序是否有解的函数是否正确。先看一下6 5 0 3 1 2 7 4 8这个排列,逆序数(忽略0)为0+1+2+3+3+0+3+0=12是偶数,跟目标状态1 2 3 4 5 6 7 8 0同奇偶,程序有解,那么这里解出22步也是验证了该函数的正确性。或者可以再来看一个无解的情况,例如4 8 1 5 0 2 6 7 3,逆序数为0+0+2+1+3+1+1+5=13是奇数,因此无解。
可以看到图1(b)的平均运行时间是比(a)中要少的。这也是可解释的。(a)的估价函数是:假定每个数码可以任意的安放,那么错位数码的数量是这个松弛问题的最小成本;(b)是假定任意两个数码可以互换,而不一定是空白数码(0)跟相邻数码互换,那么这个曼哈顿距离是最小代价;这两种代价都比实际代价要小,这才使得找到最优解成为可能。代价越大,能扩展的节点也就越少,使得程序不容易往错误的方向扩展,又由于评估代价永远小于实际代价,因此也不会漏掉最优解。而(b)的评估值是比(a)要大的,因此(b)需扩展的节点越少,越不容易走错路,效率也就更高。
越接近实际代价,扩展的路径就越接近最优解,效率也就越高。
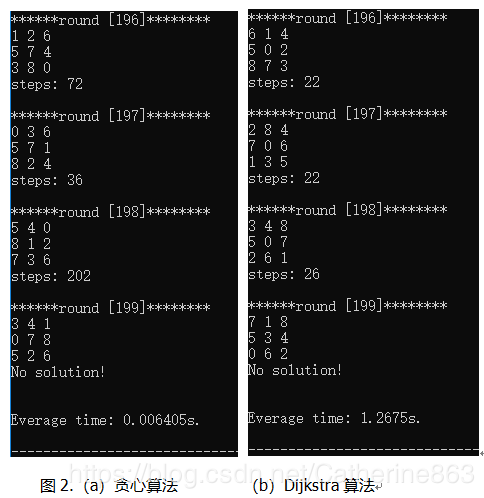
贪心搜索、Dijkstra算法与A*
贪心算法和Dijkstra最短路算法其实是A的两种极端情况,虽然题目中没要求Dijkstra算法,我这里也顺便贴上来吧。贪心算法是只考虑预估代价h,因此f=h;而Dijkstra只考虑到当前代价g,因此f=g;而A是两者都考虑,因此f=g+h。
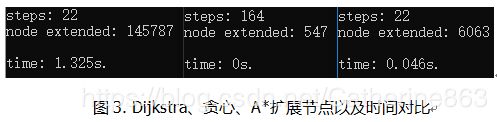
如图2(a),贪心算法因为每次只考虑离目标最近的节点,因此速度是最快的,不过它的解往往不是最优的,可以看到图中初始状态为5 4 0 8 1 2 7 3 6的解高达202步;Dijkstra考虑当前代价最小的点,需要扩展的节点量很大,虽然找到的解是最优解,但是效率很低。而A将二者结合起来,实现了既能找到最优解,效率相比于Dijkstra最短路算法又有很大的提升。
下图分别展示了Dijkstra、贪心、A的对比。可见Dijkstra扩展的节点的数量级是很恐怖的。
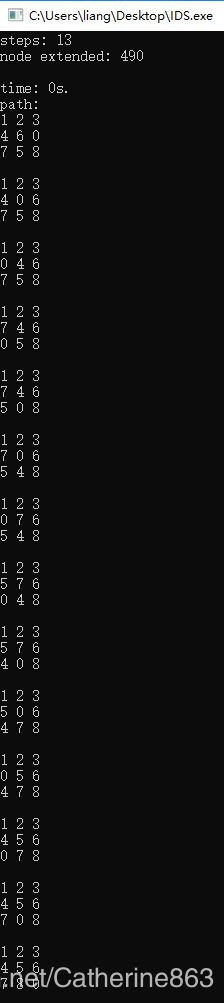
IDS
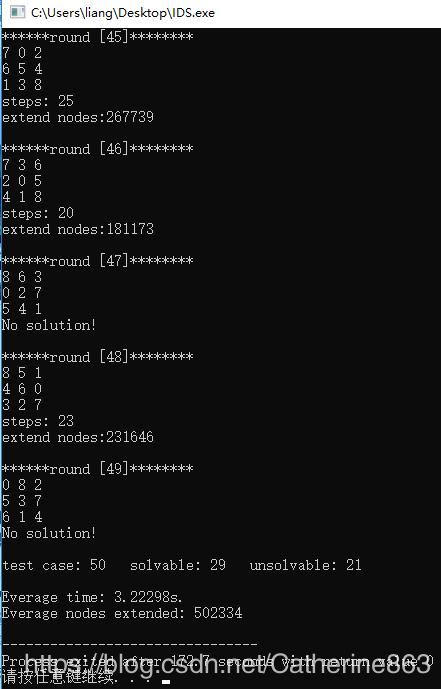
如上图所示是IDS跑50个样例的运行结果图,这里没有像A*和贪心一样跑200次,因为跑这个太耗时,跑50次也就够了,而且补充说明一下,这次的结果是在性能比较好的电脑上跑的,运行时间还需要这么多,那说明IDS在这几个方法中是最耗时的。因为IDS从深度1开始迭代,搜不到结果就增加深度继续迭代,这将会非常耗时。但是可以找到最优解,因为在最浅层找到的解代价是最小的。
迭代加深搜索通常用于那种搜索树又深又宽、但是解并不是很深的情况,这时广度优先搜索会超空间,而深度优先搜索会超时。这时迭代加深搜索很有用,可是说是在用递归方法在实现广度优先搜索。
既然用指针写了寻路路径,那就po上来给大家看一下吧~不过我new了很多个指针却没有delete掉,因为这呈现一个反向树结构,分支太多,不知道怎么delete,有懂的话还望大家不吝赐教,多谢。
最后附上全部代码:
A* / 贪心 C++代码:
#include
#include
#include
#include
#include
#include
#include
using namespace std;
//状态结构体
struct State{
State(){
}
State(const State &st){
for(int i=0;i<3;i++)
for(int j=0;j<3;j++)
matrix[i][j] = st.matrix[i][j];
zero_x=st.zero_x; zero_y=st.zero_y;
f=st.f; g=st.g; h=st.h;
parent = st.parent;
}
~State(){
parent = NULL;
}
char matrix[3][3]; //二维数组
int zero_x,zero_y; //0(即空格)的位置
int f,g,h; //代价函数f=g+h,g:起始状态到当前状态的代价,h: 估计当前状态到最终状态的代价
struct State* parent;
friend bool operator < (const State &a,const State &b){
if(a.f==b.f) return a.g<=b.g;
return a.f>=b.f;
}
};
State start; //开始状态(开始节点)
State goal; //目标状态
//启发式函数 h, 不在正确位置的格子的数目
int cal_h(State stat){
int cnt = 0; //记录当前状态跟目标状态瓦片错位的个数
for(int i=0;i<3;i++){
for(int j=0;j<3;j++){
if(stat.matrix[i][j] != goal.matrix[i][j]) cnt++;
}
}
return cnt;
}
//另一种启发式函数 h2,格子横向或竖向走到正确位置的步数,即曼哈顿距离
int cal_h2(State stat){
int manhatton = 0;
bool flag=true;
for(int i=0;i<3;i++){
for(int j=0;j<3;j++){
if(stat.matrix[i][j]==goal.matrix[i][j]) continue;
flag=true; //在goal.matrix找到当前格子就可以退出来了
for(int p=0;flag && p<3;p++){
for(int q=0;q<3;q++){
if(stat.matrix[i][j]==goal.matrix[p][q]){
manhatton += (abs(p-i)+abs(q-j));
flag=false;
break;
}
}
}
}
}
return manhatton;
}
//代价函数 f(s)=g(s)+h(s)
int f(State stat){
return stat.g+stat.h;
}
//矩阵转字符串形式,以便存储到set中方便查重
string matrix2string(char a[3][3] ){
string s="";
for(int i=0;i<3;i++){
for(int j=0;j<3;j++){
s+=a[i][j];
}
}
return s;
}
//打印二维数组
void print_matrix(char a[3][3]){
for(int i=0;i<3;i++){
for(int j=0;j<3;j++){
cout< openList; //open列表
set openSeq; //因为优先队列很难查找,因此另外开一个map来记录序列,以便查找
set closeSeq; //记录close列表里每个状态的序列字符串
int move_x[4] = {-1,0,1,0}; //上右下左
int move_y[4] = {0,1,0,-1};
int node_num;
stack stack_path; //记录路径
int AStar(State& start){
//清零
while(!openList.empty()) openList.pop();
openSeq.clear();
closeSeq.clear();
//给start节点的zero_x,zero_y赋值
find_blankTile();
start.g=0;
openList.push(start);
openSeq.insert(matrix2string(start.matrix));
int index=0;
//遍历,直到open列表为空
while(!openList.empty()){
State *curState = new State(openList.top()); //当前状态。 因为是优先队列, 所以top出来的是f值最小的
//cout<<"round: "<matrix);
//cout<<"parent"<parent<matrix)==matrix2string(goal.matrix)){
int step = curState->g;
/***
根据父节点一步步往回寻路,输出路径
*/
while(!stack_path.empty()) stack_path.pop(); //清空栈
State* p = curState;
while(p!=NULL){
stack_path.push(*p);
p = p->parent;
}
//返回所需步数
return step;
}
openList.pop(); //出队
string curSeq = matrix2string(curState->matrix); //当前状态的字符串序列
openSeq.erase(curSeq); //把当前状态从开放列表移除
closeSeq.insert(curSeq); //把当前状态移动到close列表
string nextSeq="";//下一个状态的字符串序列
for(int i=0;i<4;i++){ //四个交换方向,分别为上右下左
// cout<<"i: "<zero_x = curState->zero_x+move_x[i];
nextState->zero_y = curState->zero_y+move_y[i];
if(nextState->zero_x<0||nextState->zero_x>2||nextState->zero_y<0||nextState->zero_y>2) continue; //移动超出范围,跳过
nextState->matrix[nextState->zero_x][nextState->zero_y] = '0';//curState->matrix[curState->zero_x][curState->zero_y]; //0
nextState->matrix[curState->zero_x][curState->zero_y] = curState->matrix[nextState->zero_x][nextState->zero_y];
nextSeq = matrix2string(nextState->matrix);
if(closeSeq.find(nextSeq) != closeSeq.end()) continue; //在close列表中,跳过
nextState->g += 1;
nextState->h = cal_h2(*nextState);
nextState->f = nextState->g + nextState->h; //A*算法
//nextState->f = nextState->h; //贪心算法
//nextState->f = nextState->g; //Dijkstra算法
nextState->parent = curState;
openList.push(*nextState); //
/*
if(openSeq.find(nextSeq)==openSeq.end()){ //下一个状态不在open列表中,则加入
nextState->parent = curState;
openList.push(nextState);
}else{ //下一个状态在open列表中,则检查由当前状态到达那里是否更好。如果g更小,则把它的父亲设为当前状态,并重新计算它的g和f值
}*/
}
}
}
//打印路径
void print_path(){
State* st;
cout<<"path: "<matrix);
cout<=0;j--){
if(start_seq[j]>start_seq[i]) cnt++;
}
}
if(cnt%2==0) return true;
return false;
}
// 随即生成函数
int myrandom (int i) {
return rand()%i;
}
//生成0~8的随机整数序列,作为开始状态
void randperm()
{
vector temp;
for (int i = 0; i < 9; ++i) temp.push_back(i+'0'); //生成0~8
random_shuffle(temp.begin(), temp.end(),myrandom); //随机乱序
// for (int i = 0; i < temp.size(); i++)
// {
// cout << temp[i] << " ";
// }
for(int i=0;i<3;i++){
for(int j=0;j<3;j++){
start.matrix[i][j] = temp[i*3+j];
}
}
}
int main(){
//目标状态
char goal_matrix[3][3]={{'1','2','3'},{'4','5','6'},{'7','8','0'}};
for(int i=0;i<3;i++){
for(int j=0;j<3;j++){
goal.matrix[i][j] = goal_matrix[i][j];
}
}
// 初始化随机数种子
srand((int)time(0));
clock_t startTime,endTime;
startTime = clock();
//测试次数
int T = 200;
for(int t=0;t IDS(深度迭代搜索) C++代码:
#include
#include
#include
#include
#include
#include
#include
using namespace std;
//状态结构体
struct State{
State(){
}
State(const State &st){
for(int i=0;i<3;i++)
for(int j=0;j<3;j++)
matrix[i][j] = st.matrix[i][j];
zero_x=st.zero_x; zero_y=st.zero_y;
g=st.g;
// f=st.f; g=st.g; h=st.h;
parent = st.parent;
}
~State(){
parent = NULL;
}
char matrix[3][3]; //二维数组
int zero_x,zero_y; //0(即空格)的位置
int g; //起始状态到当前状态的代价
// int f,g,h; //代价函数f=g+h,g:起始状态到当前状态的代价,h: 估计当前状态到最终状态的代价
//int parent_idx; //父节点, 这个int指的是在对象数组的index
struct State* parent;
// friend bool operator < (const State &a,const State &b){
// if(a.f==b.f) return a.g<=b.g;
// return a.f>=b.f;
// }
};
State start; //开始状态(开始节点)
State goal; //目标状态
//矩阵转字符串形式,以便存储到set中方便查重
string matrix2string(char a[3][3] ){
string s="";
for(int i=0;i<3;i++){
for(int j=0;j<3;j++){
s+=a[i][j];
}
}
return s;
}
//打印二维数组
void print_matrix(char a[3][3]){
for(int i=0;i<3;i++){
for(int j=0;j<3;j++){
cout< > que;
int node_num;
stack stack_path; //记录路径
int IDS(int max_depth){
//初始化start节点
find_blankTile(); start.g=0; start.parent=NULL;
int depth=0; //深度
que.push(make_pair(start,depth)); //将<节点,深度>对 入栈
int curDepth,nextDepth; //当前节点深度,扩展节点深度
node_num=0; //记录总扩展节点数
while(!que.empty()){
node_num++;
State *curState = new State(que.top().first);
curDepth = que.top().second;
que.pop();
if(matrix2string(curState->matrix)==matrix2string(goal.matrix)){
int step = curState->g;
// 据父节点一步步往回寻路,存入stack_path中
while(!stack_path.empty()) stack_path.pop(); //清空栈
State* p = curState;
while(p!=NULL){
stack_path.push(*p);
p = p->parent;
}
return step;//返回所需步数
}
nextDepth = curDepth + 1;
if(nextDepth > max_depth) continue;
string curSeq = matrix2string(curState->matrix); //当前状态的字符串序列
for(int i=0;i<4;i++){
State* nextState = new State(*curState);//下一个状态.先拷贝父节点,之后再改
nextState->zero_x = curState->zero_x+move_x[i];
nextState->zero_y = curState->zero_y+move_y[i];
if(nextState->zero_x<0||nextState->zero_x>2
||nextState->zero_y<0||nextState->zero_y>2) continue; //移动超出范围,跳过
nextState->matrix[nextState->zero_x][nextState->zero_y] = '0';
nextState->matrix[curState->zero_x][curState->zero_y]
= curState->matrix[nextState->zero_x][nextState->zero_y];
//防止移回上一个状态
if(curState->parent!=NULL){ //排除初始节点,因为起始节点没有父节点
if(matrix2string(nextState->matrix)==matrix2string(curState->parent->matrix))
continue; //下个状态的字符串不能跟上个状态一样
}
nextState->g += 1;
nextState->parent = curState;
que.push(make_pair(*nextState,nextDepth));
}
}
return -1; //找不到解,返回-1
}
//打印路径
void print_path(){
State* st;
cout<<"path: "<matrix);
cout<=0;j--){
if(start_seq[j]>start_seq[i]) cnt++;
}
}
if(cnt%2==0) return true;
return false;
}
// 随即生成函数
int myrandom (int i) {
return rand()%i;
}
//生成0~8的随机整数序列,作为开始状态
void randperm()
{
vector temp;
for (int i = 0; i < 9; ++i) temp.push_back(i+'0'); //生成0~8
random_shuffle(temp.begin(), temp.end(),myrandom); //随机乱序
for(int i=0;i<3;i++){
for(int j=0;j<3;j++){
start.matrix[i][j] = temp[i*3+j];
}
}
}
int main(){
//目标状态
char goal_matrix[3][3]={{'1','2','3'},{'4','5','6'},{'7','8','0'}};
for(int i=0;i<3;i++){
for(int j=0;j<3;j++){
goal.matrix[i][j] = goal_matrix[i][j];
}
}
/*
// 初始化随机数种子
srand((int)time(0));
clock_t startTime,endTime;
startTime = clock();
//测试次数
int T = 2;
int solvable=0; //记录有解的样例数
int node_extend=0; //记录平均扩展的节点数
for(int t=0;t