NSCT(Nonsubsampled Contourlet变换)

参考:
https://blog.csdn.net/jbb0523/article/details/42689465#comments
http://blog.sina.com.cn/s/blog_5590809b0100ckcv.html
https://blog.csdn.net/hengjianle/article/details/1343818
示例代码:https://blog.csdn.net/neoyek/article/details/83684068
闫 利,向天烛
基于非下采样轮廓波变换的ＳＡＲ图像去噪算法研究 季新

一直以来偶尔都会见到这个名词却不知道具体含义,今天简要的记录一下NSCT的概念.暂时还没有运行过它的代码,具体的细节以后有机会再说.

小波变换与Contourlet变换

对于一维信号,小波变换能够比傅里叶变换更“稀疏”地表示一维分段光滑或者有界变差函数.但是小波变换在面对一维信号所具有的优异特性并不能简单的推广到二维或更高维.传统的小波变换各向同性,只具有有限个方向,且存在采样操作,缺乏平移不变性,不能很好地表示图像中的边缘方向等信息.因为一维小波张成的可分离小波(Separable wavelet)只具有有限的方向,不能“最优”地表示含线或者面奇异的高维函数,但事实上具有线或面奇异的函数在高维空间中非常普遍,例如,自然物体光滑边界使得自然图像的不连续性往往体现为光滑曲线上的奇异性,而并不仅仅是点奇异.换句话说,在高维情况下,小波分析并不能充分利用数据本身特有的几何特征,并不是最优的或者说“最稀疏”的函数表示方法.针对于小波在二维信号表示时的缺点,2002年，MN Do和Martin Vetterli提出了一种“真正”的图像二维表示方法:Contourlet变换(轮廓波变换),也称塔型方向滤波器组(Pyramidal Directional Filter Bank, PDFB).Contourlet变换是利用拉普拉斯塔形分解(LP)和方向滤波器组(DFB)实现的另一种多分辨的、局域的、方向的图像表示方法.
值得注意的是,由于多尺度分解的不完全性,低频部分仍旧会保留图像的部分细节信息,这种现象在分解层数较少时尤为突出.

Contourlet变换

Contourlet基的支撑区间是具有随尺度变化长宽比的“长条形”结构,不仅具有小波变换的多分辨率和时频局部的特性,还具有多方向性和各向异性.Contourlet系数中,表示图像边缘的系数能量更加集中.换句话说Contourlet变换对于曲线有更“稀疏”的表达.Contourlet变换将多尺度分析和方向分析分拆进行.首先由LP(Laplacian pyramid)变换对图像进行多尺度分解以“捕获”点奇异,接着由方向滤波器组(Directional Filter Bank, DFB)将分布在同方向上的奇异点合成为一个系数.
由于DFB仅适用于高频,并且会泄露其定向子带的低频信息.所以利用LP对低频信息进行分解和移除.因此,图像信号通过LP子带以获得带通信号(高频信号),并通过DFB传递这些信号以捕获图像的方向信息.这种LP和DFB组合的双滤波器组结构也称为金字塔方向滤波器组(PDFB).
通过使用轮廓波变换,可以使用少量系数有效地捕获原始图像的轮廓,其是自然图像中的主要特征.实验证明,Contourlet变换在图像降噪,纹理,形状的特征提取方面的性能比二维离散小波变换有了明显的提高.而二维小波是由一维小波张量积构建得到,它的基缺乏方向性,不具有各向异性.只能限于用正方形支撑区间描述轮廓,不同大小的正方形对应小波的多分辨率结构.当分辨率变得足够精细，小波就变成用点来捕获轮廓.

NSCT

但是轮廓波变换不具有平移不变性(shift invariant),所以在05年da Cunha，Zhou和Do提出了非下采样轮廓波变换Nonsubsampled Contourlet变换(NSCT).
Contourlet变换之所以不具有平移不变性,其原因就在于拉普拉斯金字塔和方向滤波器组中存在的上采样和下采样.为了保留变换的方向和多尺度属性,拉普拉斯金字塔被替换为非下采样金字塔结构(NSP)以保留多尺度属性,以及非下采样方向滤波器(NSDFB)组用于方向性.

NSP

非下采样轮廓波变换的多尺度分解功能的实现是利用平移不变的滤波结构得到的，这种结构类似于拉普拉斯金字塔，可以实现子带的多尺度分解。当图像经过L层非下采样金字塔分解后，可以获得L+1个子带图像，且子带图像与源图像大小相同。
非下采样金字塔分解采用双通道的非下采样滤波器组结构来实现。其结构如下所示，其中$H_0(z)$低通分解滤波器,$H_1(z)$表示高通分解滤波器；$G_0(z)$表示低通重构滤波器。$G_1(z)$表示高通重构滤波器。

在运用双通道滤波器组进行分解的过程当中，要达到对分解的完全重构这一目的，各滤波器应该满足以下关系：

NSDFB

方向滤波器组利用一个k层二叉树将频域分解成$2^k个子带，在这一过程中，频率分割的实现依赖于梅花滤波器组的扇形滤波器和平移操作，有效避免了对输入信号的调制。

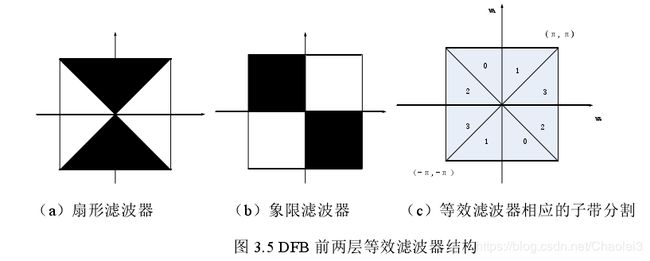
我们使用(a)(b)2个滤波器可以对图像滤波就可以生成（c）那样的子带分割。

非下采样滤波器组的结构是：一、利用扇形滤波器组和象限滤波器组将图像分为四个方向子带；二、利用平行滤波器组迭代出不同方向的子带。而每个方向子带图只表示处在那个方向内的信息，如上图中编号为0的通道，我们得到其对应的方向子带就只在0所包括的区域内有图像信息，其他区域都没有信息。而且此方向子带图同原图像大小一样。
当对图像的高频子带图像进行k层方向分解，此时就能够得到$2^k$个方向子带图像，且方向子带图像与源图像大小相同。在图像进行J层 NSCT 变换，我们可以得到 1 个低频子带图像和${\sum }_{j=1}^J{2}^{k_i}$个方向子带，其中j是分解层数，$k_i$是方向分解数。
首先由NSP对输入图像进行塔形分解,将图像分解为高通和低通两个部分,然后由NSDFB将高频子带分解为多个方向子带,低频部分继续进行如上分解.NSCT是一种新型平移不变,多尺度,多方向性的快速变换.

图中展示了NSCT的分解过程,首先应用NSP进行多尺度分解,第一层分解得到低通子带图像(Lowpass Subband Image，LSI1)和带通子带图像（Bandpass Subband Image，BSI1），第二层对第一层得到的结果LSI1 继续分解得到相应的 LSI 2和 BSI2，以此类推.需要了解的是,第一层所得到的结果 LSI 1和 BSI1 跟原始图像中的特征结构最为接近，携带的原始特征数据最多.
然后利用非下采样方向滤波器将通过 NSP多尺度分解所得的带通子带图像（BSI）进行树形分解.非下采样方向滤波器（Nonsubsampled Directional Filter Bank，NSDFB)是一个双通道的滤波器组.若对 BSI 进行k元的树形分解，则可得到 $2^k$个图像,此时 BSI 的频带会分裂成楔形.此结果图像称为带通方向子带图像(Bandpass Directional Subband Image，BDSI).