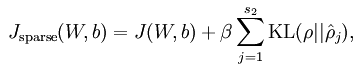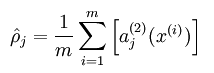Sparse-Autoencoder

作者：chen_h
微信号 & QQ：862251340
微信公众号：coderpai

---

• 自编码器 Autoencoder
• 稀疏自编码器 Sparse Autoencoder
• 降噪自编码器 Denoising Autoencoder
• 堆叠自编码器 Stacked Autoencoder

---

稀疏自编码器可以看做是自编码器的一个变种，它的作用是给隐藏神经元加入稀疏性限制，那么自编码神经网络即使在隐藏神经元数量较多的情况下任然可以返现输入数据中一些有趣的结构。

稀疏性可以被简单地解释为：如果当神经元的输出接近于1的时候我们认为它被激活，而输出接近于0的时候认为它被抑制，那么使得神经元大部分的时间都是被抑制的限制则被称作稀疏性限制。这里我们假设的神经元的激活函数是 sigmoid 函数。如果你使用 tanh 作为激活函数的话，当神经元输出为-1的时候，我们认为神经元是被抑制的。

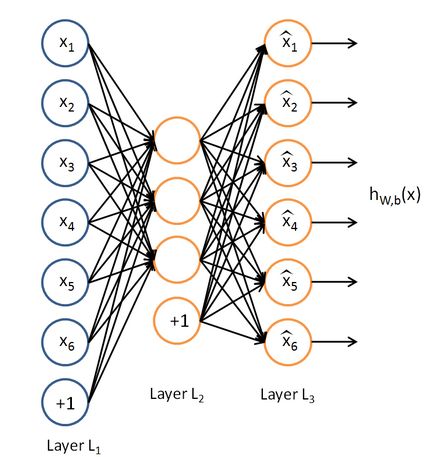
稀疏自编码器网络结果还是和自编码器一样，如下：

稀疏自编码器与自编码器的不同点在于损失函数的设计上面。稀疏编码是对网络的隐藏层的输出有了约束，即隐藏层神经元输出的平均值应尽量为0。也就是说，大部分的隐藏层神经元都处于非 activite 状态。因此，此时的 sparse autoencoder 损失函数表达式为：

最后的一项表示KL散度，其具体表达式如下：

隐藏层神经元 j 的平均活跃度计算如下：

其中，p 是稀疏性参数，通常是一个接近于0的很小的值（比如 p = 0.05）。换句话说，我们想要让隐藏层神经元 j 的平均活跃度接近 0.05 。为了满足这一条件，隐藏层神经元的活跃度必须接近于 0 。为了实现这一限制，所以我们才设计了上面的KL散度。

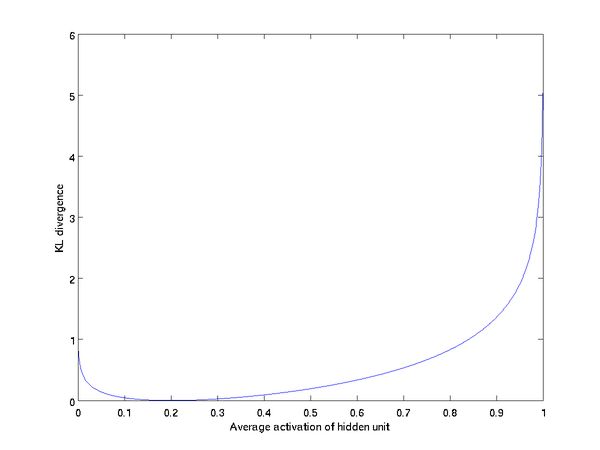
如果我们假设平均激活度 p = 0.2，那么我们就能得到下图的关系：

从图中，可以看出，当值一旦偏离期望激活度 p 时，这种误差便会急剧增大，从而作为称发现个添加到目标函数，可以指导整个网络学习出稀疏的特征表示。

实验代码如下：

#!/usr/bin/env python
# -*- coding: utf-8 -*-

import tensorflow as tf 
import numpy as np 


N_INPUT = 4
N_HIDDEN = 100
N_OUTPUT = N_INPUT
BETA = tf.constant(3.0)
LAMBDA = tf.constant(.0001)
EPSILON = .00001
RHO = .1


def diff(input_data, output_data):
    ans = tf.reduce_sum(tf.pow(tf.sub(output_data, input_data), 2))
    return ans

def main(_):

    weights = {
        'hidden': tf.Variable(tf.random_normal([N_INPUT, N_HIDDEN]), name = "w_hidden"),
        'out': tf.Variable(tf.random_normal([N_HIDDEN, N_OUTPUT]), name = "w_out")
    }

    biases = {
        'hidden': tf.Variable(tf.random_normal([N_HIDDEN]), name = "b_hidden"),
        'out': tf.Variable(tf.random_normal([N_OUTPUT]), name = "b_out")
    }

    def KLD(p, q):
        invrho = tf.sub(tf.constant(1.), p)
        invrhohat = tf.sub(tf.constant(1.), q)
        addrho = tf.add(tf.mul(p, tf.log(tf.div(p, q))), tf.mul(invrho, tf.log(tf.div(invrho, invrhohat))))
        return tf.reduce_sum(addrho)

    with tf.name_scope('input'):
        # input placeholders
        x = tf.placeholder("float", [None, N_INPUT], name = "x_input")
        #hidden = tf.placeholder("float", [None, N_HIDDEN], name = "hidden_activation")

    with tf.name_scope("hidden_layer"):
        # from input layer to hidden layer
        hiddenlayer = tf.sigmoid(tf.add(tf.matmul(x, weights['hidden']), biases['hidden']))

    with tf.name_scope("output_layer"):
        # from hidden layer to output layer
        out = tf.nn.softmax(tf.add(tf.matmul(hiddenlayer, weights['out']), biases['out']))

    with tf.name_scope("loss"):
        # loss items
        cost_J = tf.reduce_sum(tf.pow(tf.sub(out, x), 2))

    with tf.name_scope("cost_sparse"):
        # KL Divergence items
        rho_hat = tf.div(tf.reduce_sum(hiddenlayer), N_HIDDEN)
        cost_sparse = tf.mul(BETA, KLD(RHO, rho_hat))

    with tf.name_scope("cost_reg"):
        # Regular items
        cost_reg = tf.mul(LAMBDA, tf.add(tf.nn.l2_loss(weights['hidden']), tf.nn.l2_loss(weights['out'])))

    with tf.name_scope("cost"):
        # cost function
        cost = tf.add(tf.add(cost_J, cost_reg), cost_sparse)

    optimizer = tf.train.AdamOptimizer().minimize(cost)

    with tf.Session() as sess:

        init = tf.initialize_all_variables()
        sess.run(init)

        input_data = np.array([[0,0,0,1],[0,0,1,0],[0,1,0,0],[1,0,0,0]], float)

        for i in xrange(10000):
            sess.run(optimizer, feed_dict = {x: input_data})
            if i % 100 == 0:
                tmp = sess.run(out, feed_dict = {x: input_data})
                print i, sess.run(diff(tmp, input_data))

        tmp = sess.run(out, feed_dict = {x: input_data})
        print tmp


if __name__ == '__main__':
    tf.app.run()

---

Reference:

Stanford Lecture

UFLDL

SAE code