利用 Python 编写线性回归
作者:chen_h
微信号 & QQ:862251340
微信公众号:coderpai
简介
线性回归是分析两个或者多个变量之间关系的标准工具
在本文中,我们将使用 Python 包 statsmodels 来估计,解释和可视化线性回归模型。在此过程中,我们将讨论各种主题,包括:
- 简单和多元线性回归
- 可视化
- 内生性和遗漏变量偏差
- 二阶最小二乘法
简单线性回归
我们希望确定机构中的差异是否有助于解释观察到的经济结果。我们如何衡量制度差异和经济结果?
在文本中,经济结果用 1995 年人均国内生产总值代表,并根据汇率进行调整。制度差异由政治风险服务小组建立的 1985 - 1995 年平均征收保护指数代表。本文中使用的这些变量和其他数据可在 Daron Acemoglu 的网页上下载。
我们将使用 pandas 的 .read_stata() 函数将 .dta 文件中包含的数据读入数据帧。
import pandas as pd
df1 = pd.read_stata('https://github.com/QuantEcon/QuantEcon.lectures.code/raw/master/ols/maketable1.dta')
df1.head()
| shortnam | euro1900 | excolony | avexpr | logpgp95 | cons1 | cons90 | democ00a | cons00a | extmort4 | logem4 | loghjypl | baseco | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | AFG | 0.000000 | 1.0 | NaN | NaN | 1.0 | 2.0 | 1.0 | 1.0 | 93.699997 | 4.540098 | NaN | NaN |
| 1 | AGO | 8.000000 | 1.0 | 5.363636 | 7.770645 | 3.0 | 3.0 | 0.0 | 1.0 | 280.000000 | 5.634789 | -3.411248 | 1.0 |
| 2 | ARE | 0.000000 | 1.0 | 7.181818 | 9.804219 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| 3 | ARG | 60.000004 | 1.0 | 6.386364 | 9.133459 | 1.0 | 6.0 | 3.0 | 3.0 | 68.900002 | 4.232656 | -0.872274 | 1.0 |
| 4 | ARM | 0.000000 | 0.0 | NaN | 7.682482 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
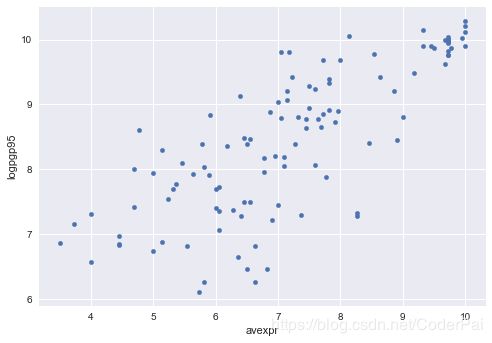
让我们用一个散点图来看一下人均 GDP 与征收指数保护之间是否存在明显的关系。
import matplotlib.pyplot as plt
plt.style.use('seaborn')
df1.plot(x='avexpr', y='logpgp95', kind='scatter')
plt.show()
该图显示了征收与人均 GDP 之间存在相当强的正相关关系。
具体而言,如果对征收的更高保护是衡量制度质量的指标,那么更好的制度似乎与更好的经济结果正相关(人均 GDP 更高)。
鉴于这种情节,选择线性模型来描述这种关系似乎是一个合理的假设。
我们可以把我们的模型写成:
l o g p g p 9 5 i = β 0 + β 1 a v e x p r i + μ i logpgp95_{i} = \beta_{0} + \beta_{1}avexpr_{i} + \mu_{i} logpgp95i=β0+β1avexpri+μi
其中,
- β 0 \beta_{0} β0 是 y 轴上线性趋势线的截距;
- β 1 \beta_{1} β1 是线性趋势线的斜率,表示保护风险对人均 GDP 的边际效应
- μ i \mu_{i} μi 是随机误差项(由于未包含在模型中的因素,观测值与线性趋势的偏差)
在视觉上,这个线性模型涉及选择最合适数据的直线,如下:
import numpy as np
# Dropping NA's is required to use numpy's polyfit
df1_subset = df1.dropna(subset=['logpgp95', 'avexpr'])
# Use only 'base sample' for plotting purposes
df1_subset = df1_subset[df1_subset['baseco'] == 1]
X = df1_subset['avexpr']
y = df1_subset['logpgp95']
labels = df1_subset['shortnam']
# Replace markers with country labels
plt.scatter(X, y, marker='')
for i, label in enumerate(labels):
plt.annotate(label, (X.iloc[i], y.iloc[i]))
# Fit a linear trend line
plt.plot(np.unique(X),
np.poly1d(np.polyfit(X, y, 1))(np.unique(X)),
color='black')
plt.xlim([3.3,10.5])
plt.ylim([4,10.5])
plt.xlabel('Average Expropriation Risk 1985-95')
plt.ylabel('Log GDP per capita, PPP, 1995')
plt.title('Figure 2: OLS relationship between expropriation risk and income')
plt.show()
估计线性模型参数( β \beta β)的最常用技术是普通最小二乘法(OLS)。
顾名思义,OLS 模型通过找到最小化残差平方和的参数来解决。即:
m i n β ^ ∑ i = 1 N μ i ^ 2 \underset{\hat{\beta}}{min} \sum_{i=1}^{N}\hat{\mu_{i}}^{2} β^min∑i=1Nμi^2
其中, μ ^ \hat{\mu} μ^ 观察值和因变量预测值之间的差异。
为了估计常数项 β 0 \beta_{0} β0 ,我们需要在数据集中添加一列 1(如果用 β 0 \beta_{0} β0 和 x i = 1 x_{i}=1 xi=1 替代 β 0 \beta_{0} β0,则考虑方程式 )
df1['const'] = 1
现在我们可以使用 OLS 函数在 statsmodels 中构建我们的模型。
我们将 pandas 函数帧与 statsmodels 一起使用,但是标准数组也可以用作参考。
import statsmodels.api as sm
reg1 = sm.OLS(endog=df1['logpgp95'], exog=df1[['const', 'avexpr']], missing='drop')
type(reg1)
statsmodels.regression.linear_model.OLS
到目前为止,我们已经构建了我们的模型。我们需要使用 .fit() 来获得参数估计 β 0 ^ \hat{\beta_{0}} β0^ 和 β 1 ^ \hat{\beta_{1}} β1^ 。
results = reg1.fit()
type(results)
statsmodels.regression.linear_model.RegressionResultsWrapper
我们现在将拟合的回归模型存储在结果中。要查看 OLS 回归结果,我们可以调用 .summary() 方法。
print(results.summary())
OLS Regression Results
==============================================================================
Dep. Variable: logpgp95 R-squared: 0.611
Model: OLS Adj. R-squared: 0.608
Method: Least Squares F-statistic: 171.4
Date: Mon, 19 Nov 2018 Prob (F-statistic): 4.16e-24
Time: 17:03:03 Log-Likelihood: -119.71
No. Observations: 111 AIC: 243.4
Df Residuals: 109 BIC: 248.8
Df Model: 1
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
const 4.6261 0.301 15.391 0.000 4.030 5.222
avexpr 0.5319 0.041 13.093 0.000 0.451 0.612
==============================================================================
Omnibus: 9.251 Durbin-Watson: 1.689
Prob(Omnibus): 0.010 Jarque-Bera (JB): 9.170
Skew: -0.680 Prob(JB): 0.0102
Kurtosis: 3.362 Cond. No. 33.2
==============================================================================
Warnings:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
从结果中,我们可以看到:
- 截距 β 0 ^ = 4.63 \hat{\beta_{0}} = 4.63 β0^=4.63
- 斜率 β 1 ^ = 0.53 \hat{\beta_{1}} = 0.53 β1^=0.53
- 正的 β 1 ^ \hat{\beta_{1}} β1^ 参数估计意味着制度质量对经济结果有积极影响
- β 1 ^ \hat{\beta_{1}} β1^ 的 p 值为 0.000 意味着制度对 GDP 的影响具有统计显著性(使用 p< 0.05 作为拒绝规则)
- R平方值 0.611
使用我们的参数估计,我们现在可以将我们的估计关系写为:
l o g p g p 9 5 i ^ = 4.63 + 0.53 a v e x p r i \hat{logpgp95_{i}} = 4.63+0.53avexpr_{i} logpgp95i^=4.63+0.53avexpri
上述的方程是对我们数据的最好的拟合,正如图二描述的。
我们能使用这个等式去对我们的数据进行预测,比如当我们的 avexpr 为 7.07 时,我们就可以得到对数 GDP 为 8.38。
mean_expr = np.mean(df1_subset['avexpr'])
mean_expr
6.515625
predicted_logpdp95 = 4.63 + 0.53 * 7.07
predicted_logpdp95
8.3771
获得此结果的一种更加简单(也更加准确)的方法是使用 .predict() 并设置 constat=1 和 avexpri = mean_expr 。
results.predict(exog=[1, mean_expr])
array([8.09156367])
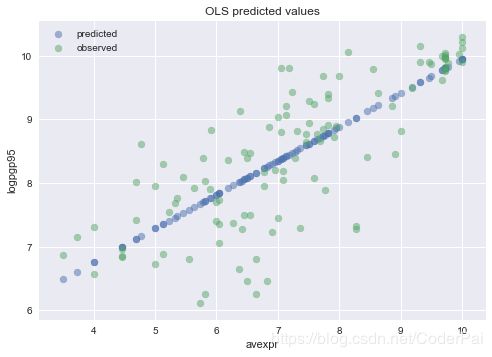
我们可以通过在结果上调用 .predict() 来获取数据集中 avexpri 的每个值的预测 logpgp95i 数组。
根据 avexpri 绘制预测值,表明预测值位于我们上面拟合的线性线上。
为了比较目的,还绘制了 logpgp95i 的观察值。
# Drop missing observations from whole sample
df1_plot = df1.dropna(subset=['logpgp95', 'avexpr'])
# Plot predicted values
plt.scatter(df1_plot['avexpr'], results.predict(), alpha=0.5, label='predicted')
# Plot observed values
plt.scatter(df1_plot['avexpr'], df1_plot['logpgp95'], alpha=0.5, label='observed')
plt.legend()
plt.title('OLS predicted values')
plt.xlabel('avexpr')
plt.ylabel('logpgp95')
plt.show()
来源:https://lectures.quantecon.org/py/ols.html