机器学习项目构建
前言
构建机器学习项目,包含主要的学习步骤:
1、 数据清理和格式化;
2、 探索性数据分析;
3、 特征工程和特征选择;
4、 在性能指标上比较学习模型;
5、 对最佳模型执行超参数调整;
6、 解释模型结果;
7、 结果分析;
从数据清理,到数据分析,到特征工程,再到Baseline的构建。逐步熟悉机器学习的构建过程。在整体上,构建机器学习的项目都很相似。该项目的总体实现有利于今后对机器学习项目的进一步研究和开发。
一、 碎片拼接
机器学习的常见工作流程::
1、数据清理和格式化
2、探索性数据分析
3、特征工程和特征选择
4、在性能指标上比较机器学习模型
5、对最佳模型执行超参数调整
6、在测试集中评估最佳模型
7、解释模型结果
8、结论汇总
1.1 问题定义
把实际问题抽象成可以解决的问题,可行的问题解决方案和可用的合理数据是项目开发的第一步工作也是最为关键的一步!
说明:使用的公共数据为建筑能源数据。
目标是使用能源数据建立一个模型,来预测建筑物的Energy Star Store(能源星级分数),并解释结果以找到评分的因素。
数据包括Energy Star Storeà属于监督学习的范畴。
监督:对数据的特征和目标明确,目标是训练可以学习两者之间映射关系的模型。
回归:Energy Star Store是一个连续变量。
模型建立:在准确性上à可以实现预测EnergyStar Store,并且结果接近真实值。
在解释上à可以理解模型的预测。
1.2 数据清洗
并非每个数据集都是完美的观测数据,没有缺失值或异常值。现实世界的数据十分杂乱,这意味着我们在开始分析之前,需要对数据清理并将其转化为可接受的数据格式。数据清理是大多数实际数据科学问题中最容易忽视,但却必不可少的一部分。
1.3 缺少数据和异常值
除了不正确的数据集外,处理真实世界数据时的另一个常见的问题是缺失值。因此在训练机器学习模型之前必须填写数据或删除数据。
尽管我们总是希望小心删除信息,但如果列中缺失值的比例很高,那么它对我们的模型可能不会有用。删除列的阈值应该取决于实际问题,并且对于此项目,我们将删除缺失值超过50%的列。
1.4 探索性数据分析
较为繁琐的数据清理部分处理完成之后,我们可以继续探索我们的数据。探索性数据分析(EDA)是一个开放的过程,我们可以计算统计数据,并通过画图分析发现数据中的趋势、异常、模型和关系。
EDA的目标是了解我们的数据,并可以从数据中得到社么。它通常以高层概述开始,在我们发现有趣的数据后,再缩小到特定的区域。这些发现有助于我们的建模选择和帮助我们决定使用哪些特。
1.5 单变量图
目标是预测Enery Star Store,所以合理的开始是检测此变量的分布。直方图是可视化单个变量分布行之有效的方法,使用matplotlib十分方便。
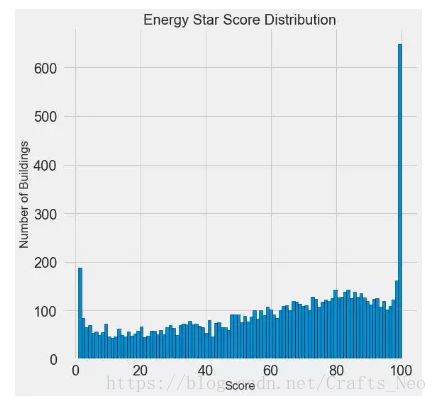
import matplotlib.pyplot as plt # Histogram of the Energy Star Score plt.style.use('fivethirtyeight') plt.hist(data['score'].dropna(), bins = 100, edgecolor = 'k'); plt.xlabel('Score'); plt.ylabel('Number of Buildings'); plt.title('Energy Star Score Distribution');
这看起来很可疑! Energy Star Score是百分位数,这意味着我们期望看到一个统一的分布,即每个得分分配给相同数量的建筑物。然而,不成比例的建筑物具有最高的100分或最低的1分(对于EnergyStar Score来说更高表示越好)。
如果我们回到score的定义,我们会看到它基于“自我报告能量使用”,这可能解释了分数偏高——要求建筑物所有者报告自己的能源使用情况就像要求学生在测试中报告自己的分数! 因此,这可能不是衡量建筑能效的最客观标准。
如果我们有无限的时间,我们可能想要调查为什么这么多建筑物有非常高和非常低的分数——我们可以通过选择这些建筑物并查看它们的共同点。但是,我们的目标只是预测分数,而不是设计更好的建筑物评分方法!我们可以在我们的报告中记下分数具有可疑分布,但我们主要关注预测分数。
1.6 寻找关系
、EDA的主要部分是搜索特征和目标之间的关系。与目标相关的变量对模型很有用,因此它们可用于测试目标。这里使用的是seaborn的密度图,可以检测目标上的分类变量。
密度图可以被认为是平滑的直方图,因为它显示了单个变量的分布。我们可以按类别对密度图进行着色,以查看分类变量如何改变分布。下面代码是创建了一个用建筑物类型(仅限于具有超过100个数据点的建筑物类型)着色的Energy Star Score密度图:
# Create a list of buildings with more than 100 measurements types = data.dropna(subset=['score']) types = types['Largest Property Use Type'].value_counts() types = list(types[types.values > 100].index) # Plot of distribution of scores for building categories figsize(12, 10) # Plot each building for b_type in types: # Select the building type subset = data[data['Largest Property Use Type'] == b_type] # Density plot of Energy Star scores sns.kdeplot(subset['score'].dropna(), label = b_type, shade = False, alpha = 0.8); # label the plot plt.xlabel('Energy Star Score', size = 20); plt.ylabel('Density', size = 20); plt.title('Density Plot of Energy Star Scores by Building Type', size = 28);
我们可以看到建筑类型对Energy Star Score有重大影响。 办公楼往往有较高的分数,而酒店的分数较低。这告诉我们,我们应该在建模中包含建筑类型,因为它确实对目标有影响。作为分类变量,我们将不得不对建筑物类型进行one-hot编码。
同上,可以显示自治市镇的Energy Star Score:
自治市镇对建筑类型的评分似乎没有太大的影响。 尽管如此,我们可能希望将其纳入我们的模型中,因为各区之间存在细微的差异。
为了量化变量之间的关系,我们可以使用Pearson相关系数。它可以用来衡量两个变量之间的线性关系的强度和方向。 +1分是完美的线性正相关关系,-1分是完美的负线性关系。 相关系数的几个值如下所示:
虽然相关系数无法捕捉非线性关系,但它是开始计算变量如何相关的好方法。 在Pandas中,我们可以轻松计算数据框中任何列之间的相关性:
#Find all correlations with the score and sort
correlations_data =data.corr()['score'].sort_values()
1.7 双变量图
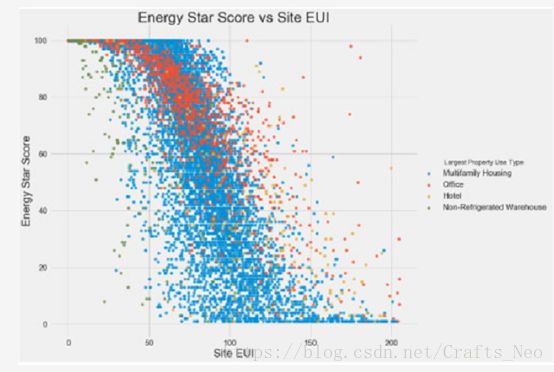
为了可视化两个变量之间的关系,我们可以使用散点图。我们可以在点的颜色中包含附加信息,如分类变量。下图显示的是不同建筑我类型的Energy Star Store与site EUI的关系:
这个图让我们可以看到-0.7的相关系数。 随着Site EUI减少,Energy Star Score增加,这种关系在建筑类型中保持稳定。
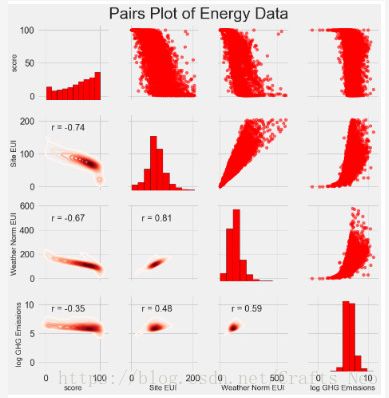
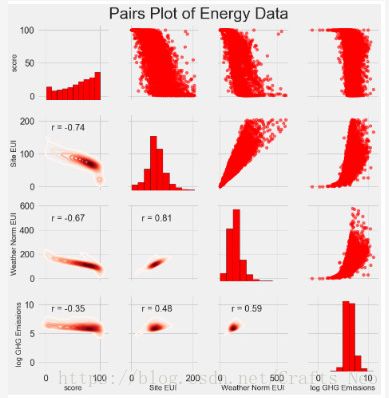
我们将做的最后的探索性plot被称为PairsPlot。这是一个很好的探索工具,因为它可以让我们看到多个变量对之间的关系以及单个变量的分布。在这里,我们使用seaborn可视化库和PairGrid函数来创建上三角上具有散点图的配对图,对角线上的直方图以及下三角形上的二维核密度图和相关系数。
# Extract the columns to plot plot_data = features[['score', 'Site EUI (kBtu/ft²)', 'Weather Normalized Source EUI (kBtu/ft²)', 'log_Total GHG Emissions (Metric Tons CO2e)']] # Replace the inf with nan plot_data = plot_data.replace({np.inf: np.nan, -np.inf: np.nan}) # Rename columns plot_data = plot_data.rename(columns = {'Site EUI (kBtu/ft²)': 'Site EUI', 'Weather Normalized Source EUI (kBtu/ft²)': 'Weather Norm EUI', 'log_Total GHG Emissions (Metric Tons CO2e)': 'log GHG Emissions'}) # Drop na values plot_data = plot_data.dropna() # Function to calculate correlation coefficient between two columns def corr_func(x, y, **kwargs): r = np.corrcoef(x, y)[0][1] ax = plt.gca() ax.annotate("r = {:.2f}".format(r), xy=(.2, .8), xycoords=ax.transAxes, size = 20) # Create the pairgrid object grid = sns.PairGrid(data = plot_data, size = 3) # Upper is a scatter plot grid.map_upper(plt.scatter, color = 'red', alpha = 0.6) # Diagonal is a histogram grid.map_diag(plt.hist, color = 'red', edgecolor = 'black') # Bottom is correlation and density plot grid.map_lower(corr_func); grid.map_lower(sns.kdeplot, cmap = plt.cm.Reds) # Title for entire plot plt.suptitle('Pairs Plot of Energy Data', size = 36, y = 1.02);
要查看变量之间的交互,我们查找行与列相交的位置。例如,要查看Weather EUormEUI与score的相关性,我们查看Weather EUormEUI行和score列,并查看相关系数为-0.67。
1.8 特征工程和选择
特征工程和选择通常会为机器学习问题投入最大的时间。
定义:
● 特征工程:获取原始数据并提取或创建新特征的过程。这可能意味着需要对变量进行变换,例如自然对数和平方根,或者对分类变量进行one-hot编码,以便它们可以在模型中使用。 一般来说,特征工程是从原始数据创建附加特征。
● 特征选择:选择数据中最相关的特征的过程。在特征选择中,我们删除特征以帮助模型更好地总结新数据并创建更具可解释性的模型。一般来说,特征选择是减去特征,所以我们只留下那些最重要的特征。
机器学习模型只能从我们提供的数据中学习,因此确保数据包含我们任务的所有相关信息至关重要。如果我们没有给模型提供正确的数据,那么我们将它设置为失败,我们不应该期望它学习!
1.8.1 特征工程
功能设计步骤:
● One-hot编码分类变量(borough and property use type)。
● 添加数值变量的自然对数转换。
在模型中,分类变量的One-hot编码是必要的。机器学习算法无法理解像“office”这样的建筑类型,因此如果建筑物是办公室,则必须将其记录为1,否则将其记录为0。
添加转换特征可以帮助我们的模型学习数据中的非线性关系。采用平方根,自然对数或特征的次幂是数据科学中的常见做法,也是基于领域知识或在实践中最有效的方法。这里我们将使用数字特征的自然对数。
选择数字特征,对这些特征进行对数转换,选择两个分类特征,对这些特征进行one-hot编码,然后将两个特征结合在一起。
# Copy the original data features = data.copy() # Select the numeric columns numeric_subset = data.select_dtypes('number') # Create columns with log of numeric columns for col in numeric_subset.columns: # Skip the Energy Star Score column if col == 'score': next else: numeric_subset['log_' + col] = np.log(numeric_subset[col]) # Select the categorical columns categorical_subset = data[['Borough', 'Largest Property Use Type']] # One hot encode categorical_subset = pd.get_dummies(categorical_subset) # Join the two dataframes using concat # Make sure to use axis = 1 to perform a column bind features = pd.concat([numeric_subset, categorical_subset], axis = 1)
在这个过程之后,我们有超过11,000个具有110列(特征)的观测值(建筑物)。并非所有这些特征都可能对预测Energy StarScore有用,所以现在我们将转向特征选择从而去除一些变量。
1.8.2 特征选择
我们数据中的110个特征中的许多特征是多余的,因为它们彼此高度相关。 例如,以下是Site EUI与Weather Normalized SiteEUI的相关系数为0.997的图。
相互强相关的特征被称为共线,消除这些特征对中的一个变量通常可以帮助机器学习模型推广并更易于解释(此处讨论的是特征与其他特征的相关性,并非与目标的相关性)。
有许多方法可以计算特征之间的共线性,其中最常见的是方差扩大因子。在这个项目中,我们将使用相关系数来识别和删除共线特征。如果它们之间的相关系数大于0.6,我们将放弃一对特征中的一个。
特征选择后剩下64个特征和一个目标
# Remove any columns with all na values features = features.dropna(axis=1, how = 'all') print(features.shape) (11319, 65)
1.9 建立Baseline
我们现在已经完成了数据清理,探索性数据分析和特征工程。开始建模之前要做的最后一步是建立一个Baseline。这实际上是我们可以比较我们的结果的一种猜测。如果机器学习模型没有超越这个猜测,那么我们可能必须得出结论,机器学习对于任务来说是不可接受的,或者我们可能需要尝试不同的方法。
对于回归问题,合理的Baseline是猜测测试集中所有示例的训练集上目标的中值。这设置了一个任何模型都要超越的相对较低的标准。
我们将使用的度量标准是平均绝对误差(Mean Absolute Error)(MAE),它测量预测的平均绝对误差。有很多回归的指标,如Andrew Ng的建议【1】,选择一个指标,然后在评估模型时坚持使用它。平均绝对误差很容易计算,并且可以解释。
在计算Baseline之前,我们需要将我们的数据分成一个训练集和一个测试集:
1. 训练集是我们在训练期间给我们的模型提供特征以及答案的。目的是让模型学习特征与目标之间的映射。
2. 测试集的特征用于评估训练的模型。模型不允许查看测试集的答案,并且只能使用特征进行预测。我们知道测试集的答案,因此我们可以将测试预测与答案进行比较。
我们将使用70%的数据进行训练,30%用于测试:
# Split into 70% training and 30% testing set X, X_test, y, y_test = train_test_split(features, targets, test_size = 0.3, random_state = 42)
计算出Baseline的性能:
# Function to calculate mean absolute error def mae(y_true, y_pred): return np.mean(abs(y_true - y_pred)) baseline_guess = np.median(y) print('The baseline guess is a score of %0.2f' % baseline_guess) print("Baseline Performance on the test set: MAE = %0.4f" % mae(y_test, baseline_guess))
The baseline guess is a score of 66.00 Baseline Performance on the test set: MAE = 24.5164
Baseline的估计在测试集中约为25分。得分范围从1到100,所以这代表25%的误差,相当低的一个超越!
1.10 结论
机器学习问题的三个步骤。在定义问题之后:
1. 清理并格式化原始数据
2. 进行探索性数据分析以了解数据集
3. 开发了一系列我们将用于模型的特征
二、模型选择、超参数调整和评估
ModelSelection、Hyperparameter Tuning && Evaluation
2.1 模型评估和选择(Model Evaluation andSelection)
我们研究的是一个有监督的回归任务(a supervised regression task):利用纽约市建筑能源数据(New York City building energy data),我们想开发一个模型,可以预测建筑物的能源之星得分(Energy Star Score)。我们关注的重点是预测的准确性和模型的可解释性。
有大量的机器学习模型可供选择,这会让你难以决定从哪里开始。虽然有些图表试图告诉你要使用哪种算法,但我更愿意多尝试几种算法,并查看哪种算法效果最好!机器学习仍然是一个主要由经验(实验)而不是理论结果驱动的领域,事先知道哪种模型最好,几乎是不可能的。
一般来说,从简单的可解释模型(如线性回归)开始是一个好办法,如果性能不足,继而转向更复杂但通常更准确的模型。下图显示了一种版本的准确性与可解释性之间的权衡:
我们将评估五种不同的模型:
• 线性回归(Linear Regression)
• K最近邻回归(K-Nearest Neighbors Regression)
• 随机森林回归(Random Forest Regression)
• 梯度增强回归(Gradient Boosted Regression)
• 支持向量机回归(Support Vector Machine Regression)
2.2 填补缺失值(Imputing Missing Values)
虽然我们在处理数据时丢失了超过50%缺失值的列,但仍有不少观察结果丢失。机器学习模型无法处理任何缺失值,因此我们必须把它们填充进去,这是一个称为Imputing的过程【2】。
首先,读入所有数据,观测数据结构:
import pandas as pd import numpy as np # Read in data into dataframes train_features = pd.read_csv('data/training_features.csv') test_features = pd.read_csv('data/testing_features.csv') train_labels = pd.read_csv('data/training_labels.csv') test_labels = pd.read_csv('data/testing_labels.csv') Training Feature Size: (6622, 64) Testing Feature Size: (2839, 64) Training Labels Size: (6622, 1) Testing Labels Size: (2839, 1)
显示NaN的值都代表缺少观察结果。虽然有很多方法可以填补缺失数据,但我们将使用一种相对简单的方法,即中值插补法(median imputation)。这将使用该列的中值(the medianvalue)替换列中的所有缺失值。
在下面的代码中,我们创建了一个Scikit-Learn Imputer对象,并将strategy设置为median。 然后我们在训练数据上训练这个对象(使用imputer.fit),并用它来填充训练和测试数据中的缺失值(使用imputer.transform)。这意味着测试数据中的缺失值将填入训练数据的相应中值。
(我们必须这样做插补(imputation),而不是对所有数据进行训练,这样做是为了避免测试数据泄漏问题(testdata leakage),测试数据集中的信息会溢出到训练数据中。)
# Create an imputer object with a median filling strategy imputer = Imputer(strategy='median') # Train on the training features imputer.fit(train_features) # Transform both training data and testing data X = imputer.transform(train_features) X_test = imputer.transform(test_features) Missing values in training features: 0 Missing values in testing features: 0
现在所有的特征都具有真实的,有限的值,没有缺失值。
2.3 特征缩放(Feature Scaling)
缩放(Scaling)是指改变特征范围的一般过程。这是必要的,因为特征是以不同单位测量的,因此涵盖了不同的范围。比如支持向量机(svm)和考虑到观测之间的距离度量的K-近邻的方法,这两种方法显著地受到特征范围的影响,Scaling使得他们可以学习(learn)。尽管线性回归和随机森林等方法实际上并不需要特征缩放,但在比较多种算法时采取这一步骤仍然是最佳做法。
我们将每个特征缩放至0-1之间。通过获取每个特征值,减去特征中的最小值并除以最大值减去最小值(范围)来完成。这种缩放通常称为归一化(normalization),或者标准化(standardization)。
虽然这个过程很容易通过人工计算实现,但我们可以在Scikit-Learn中使用MinMaxScaler对象来完成。此方法的代码与imputation相同,除了使用scaler来代替imputer!再次,我们确保仅使用训练数据进行训练,之后再转换所有数据。
# Create the scaler object with a range of 0-1 scaler = MinMaxScaler(feature_range=(0, 1)) # Fit on the training data scaler.fit(X) # Transform both the training and testing data X = scaler.transform(X) X_test = scaler.transform(X_test)
现在,每个特征的最小值为0,最大值为1。缺少值插补(Missing valueimputation)和特征缩放(feature scaling)是几乎所有机器学习流程所需的两个步骤,因此很有必要理解它们的工作原理!
2.4 在Scikit-Learn中实现机器学习模型(ImplementingMachine Learning Models in Scikit-Learn)
在我们花费大量时间对数据进行清理和格式化之后,实际创建,训练和预测模型相对简单。我们将在Python中使用Scikit-Learn库,它有着很好的说明文档和一致的模型构建语法。一旦你知道如何在Scikit-Learn中创建一个模型,你就可以快速实现各种算法。
我们通过一个例子来说明如何进行模型的创建,训练(.fit)和测试(.predict),使用Gradient Boosting Regressor:
from sklearn.ensemble import GradientBoostingRegressor # Create the model gradient_boosted = GradientBoostingRegressor() # Fit the model on the training data gradient_boosted.fit(X, y) # Make predictions on the test data predictions = gradient_boosted.predict(X_test) # Evaluate the model mae = np.mean(abs(predictions - y_test)) print('Gradient Boosted Performance on the test set: MAE = %0.4f' % mae) Gradient Boosted Performance on the test set: MAE = 10.0132
模型的创建,训练和测试都是一条线!构建其他模型,我们使用相同的语法,只改变算法的名称。结果如下:
为了使这些数字正确,用目标的中值计算的朴素baseline是24.5。显然,机器学习适用于我们的问题,因为相比于baseline有显著的提高!
梯度增强回归(MAE = 10.013)略优于随机森林(MAE = 10.014)。这些结果并不完全公平,因为我们主要使用了超参数的默认值。特别是在支持向量机等模型中,性能高度依赖于这些设置。最终,从这些比较的结果中,我们将选择梯度增强回归(gradient boosted regressor)模型来进行模型优化。
2.5 模型优化的超参数调整(HyperparameterTuning for Model Optimization)
在机器学习中,在我们选择了一个模型后,我们可以通过调整模型超参数来对我们的问题进行优化。
首先,超参数是什么,它们与参数有什么不同?【4】
• 模型超参数(hyperparameters)被认为是机器学习算法的最好设置,该算法是由数据科学家在训练之前设置的。例如,随机森林中树木的数量,或者k -最近邻居算法中使用的邻居数。
• 模型参数(parameters)是模型在训练过程中学习的内容,例如线性回归中的权重。
通过改变模型中欠拟合和过拟合的平衡来控制影响模型性能的超参数。当我们的模型不够复杂(它没有足够的自由度)来学习从特征到目标的映射时,就是欠拟合(Underfitting)。一个欠拟合的模型有很高的偏置(bias),我们可以改变我们的模型使其更复杂来纠正。
过拟合(Overfitting)是当我们的模型基本上拟合了所有训练数据点的时候。过拟合模型具有很高的方差(variance),我们可以通过正则化(regularization)来限制模型的复杂性来纠正。欠拟合和过拟合模型都不能很好地适用于测试数据(testdata)。
•选择正确的超参数的问题在于,对于每个机器学习问题,最优集都会有所不同!因此,找到最佳设置的唯一方法是在每个新数据集上尝试一些设置。幸运的是,Scikit-Learn有许多方法可以让我们高效地评估超参数。此外,EpistasisLab的TPOT等项目正试图使用遗传编程(geneticprogramming)等方法优化超参数搜索。在这个项目中,我们将使用Scikit-Learning来完成这一任务,但是我们将继续关注自动ML场景中的更多工作。
2.6 随机搜索与交叉验证(Random Search with Cross Validation)
我们将要实现的特定超参数调整方法称为随机搜索和交叉验证:
• 随机搜索(Random Search)是指我们用来选择超参数的技术。我们定义一个网格,然后随机抽样不同的组合,而不是网格搜索(grid search),我们会彻底地尝试每一个组合。(令人惊讶的是,随机搜索的结果几乎和网格搜索一样,但大大缩短了运行时间。)
• 交叉验证(Cross Validation)是我们用来评估所选超参数组合的技术。 我们使用K折交叉验证,而不是将训练集分成单独的训练集和验证集,这会减少我们可以使用的训练数据量。交叉验证涉及到将训练数据分成K个folds,然后经历一个迭代过程,在这个迭代过程中,我们首先训练前K-1个folds的数据,然后在第K个fold的数据上进行评估表现。我们重复这个过程K次,在K-fold交叉验证结束时,我们将每个K次迭代的平均误差作为最终的性能度量。
K = 5的K-fold交叉验证的过程如下所示:
使用交叉验证执行随机搜索的整个过程是:
1.建立一个待评估超参数网格
2.随机抽样一组超参数
3.用选定的组合创建一个模型
4.使用K-fold交叉验证评估模型
5.确定哪些超参数运行得最好
在此使用Scikit-Learn的RandomizedSearchCV处理所有的工作!
2.6.1 Gradient Boosted Methods(梯度增强方法)
由于我们将使用梯度增强回归模型,该模型是一个集成方法,这意味着它是由许多弱的学习器(weak learners)构建的,在这个例子中是决策树(individual decision trees)。诸如随机森林之类的bagging算法会对弱的学习器进行并行训练,并让他们投票(vote)进行预测,但像梯度增强这样的方法,将会依次训练学习器,并且每个学习器都“集中了”前面的所有错误。
增强方法近年来越来越流行,并且频繁赢得机器学习竞赛。梯度增强方法(Gradient Boosting Method)是一种特殊的实现,它使用梯度下降,基于前面的残差进行连续训练来最小化成本函数。scikit-learn实现的梯度增强通常被认为效率低于XGBoost等其他库,但它对于我们的小数据集来说足够好,并且相当准确。
2.6.2 回归超参数调整(Back to HyperparameterTuning)
在Gradient Boosted Regressor中有许多超参数可以调整(tune)。在这个项目中,我们将优化以下超参数:
•loss:用来最小化的损失函数。
•n_estimators:弱学习器(决策树)的使用数量。
•max_depth:每个决策树的最大深度。
•min_samples_leaf:决策树的叶节点所需的最小示例数量。
•min_samples_split:拆分决策树节点所需的最小示例数量。
•max_features:用于拆分节点的最大特征数。
我不确定是否有人真正了解所有这些超参数之间的相互作用,找到最佳组合的唯一方法就是try!
在下面的代码中,我们构建一个超参数网格,创建一个RandomizedSearchCV对象,并在超过25个不同的超参数组合中使用4-fold交叉验证来执行超参数搜索:
# Loss function to be optimized loss = ['ls', 'lad', 'huber'] # Number of trees used in the boosting process n_estimators = [100, 500, 900, 1100, 1500] # Maximum depth of each tree max_depth = [2, 3, 5, 10, 15] # Minimum number of samples per leaf min_samples_leaf = [1, 2, 4, 6, 8] # Minimum number of samples to split a node min_samples_split = [2, 4, 6, 10] # Maximum number of features to consider for making splits max_features = ['auto', 'sqrt', 'log2', None] # Define the grid of hyperparameters to search hyperparameter_grid = {'loss': loss, 'n_estimators': n_estimators, 'max_depth': max_depth, 'min_samples_leaf': min_samples_leaf, 'min_samples_split': min_samples_split, 'max_features': max_features} # Create the model to use for hyperparameter tuning model = GradientBoostingRegressor(random_state = 42) # Set up the random search with 4-fold cross validation random_cv = RandomizedSearchCV(estimator=model, param_distributions=hyperparameter_grid, cv=4, n_iter=25, scoring = 'neg_mean_absolute_error', n_jobs = -1, verbose = 1, return_train_score = True, random_state=42) # Fit on the training data random_cv.fit(X, y)
在执行搜索之后,我们可以检查RandomizedSearchCV对象以找到最佳模型
# Find the best combination of settings random_cv.best_estimator_ GradientBoostingRegressor(loss='lad', max_depth=5, max_features=None, min_samples_leaf=6, min_samples_split=6, n_estimators=500)
然后, 我们可以使用这些结果来执行网格搜索, 方法是选择接近这些最优值的网格参数。但是, 进一步调整不太可能显著改善我们的模型。作为一般规则, 适当的特征工程(feature engineering)对模型性能的影响要比最广泛的超参数调整更大。这是机器学习中的收益递减法则:特征工程在大多数情况下会对实现目标有很大的帮助, 而超参数调整通常只会带来很小的收益。
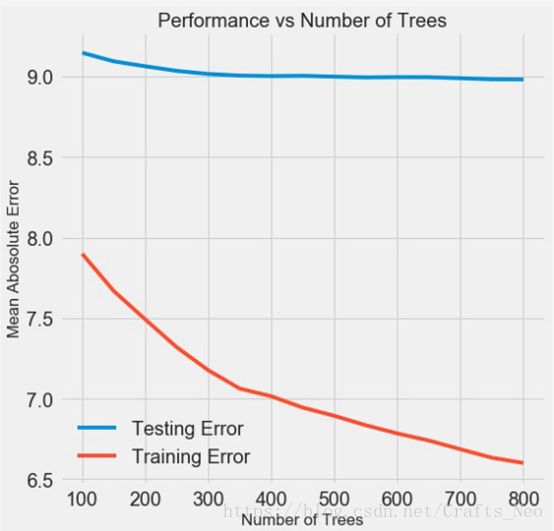
我们可以尝试的一个实验是改变估计器(决策树)的数量, 同时保持其他超参数稳定。这直接让我们观察到这个特定设置的效果。结果显示如下:
随着模型使用的树的数量增加,训练和测试的误差都会减少。 但是,训练误差比测试误差下降得快得多,我们可以看到我们的模型过拟合了:它在训练数据上表现非常好,但在测试集上无法达到相同的性能。
我们总是期望在测试集上的表现或多或少会有所下降,但是测试集和训练集的差距太显著则表明过拟合。我们可以通过获取更多训练数据来解决过度拟合问题,或者通过超参数来降低模型的复杂性。在这种情况下,我们将超参数保留在原来的位置,大家应该尝试任何可行的方法来减少过拟合。
对于最终模型,我们将使用800个估计器(estimators),因为这得到了在交叉验证中的最低误差。以下就是测试模型的阶段!
2.7 在测试集进行评估(Evaluating on the TestSet)
作为负责任的机器学习工程师,我们确保不让我们的模型在任何训练点上看到测试集的数据。因此,我们可以使用测试集的表现作为我们的模型在现实世界中部署时的表现。
对测试集进行预测并计算性能是相对简单的。在这里,我们将比较默认的梯度增强回归器(the default Gradient Boosted Regressor)与调参之后的模型的性能:
# Make predictions on the test set using default and final model default_pred = default_model.predict(X_test) final_pred = final_model.predict(X_test) Default model performance on the test set: MAE = 10.0118. Final model performance on the test set: MAE = 9.0446.
超参数调整将模型的准确率提高了约10%。这取决于使用情况,10%可能是一个巨大的改进,但它需要大量的时间投入!
我们也可以使用Jupyter Notebooks中的%timeit命令来计算训练这两个模型(默认模型和调参后模型)需要多长时间。首先是默认模型:
%%timeit -n 1 -r 5 default_model.fit(X, y) 1.09 s ± 153 ms per loop (mean ± std. dev. of 5 runs, 1 loop each)
1秒的训练时间似乎挺合理的。最终的调参后的模型并没有那么快:
%%timeit -n 1 -r 5 final_model.fit(X, y) 12.1 s ± 1.33 s per loop (mean ± std. dev. of 5 runs, 1 loop each)
这证明了机器学习的一个基本特点:它总是一种权衡的游戏。我们必须不断平衡准确性与可解释性,偏差与方差,准确性与运行时间等。这些将最终取决于所要解决的问题。在我们的例子中,相对而言,运行时间增加了12倍是很大的,但从绝对意义上讲,它并没有那么重要。
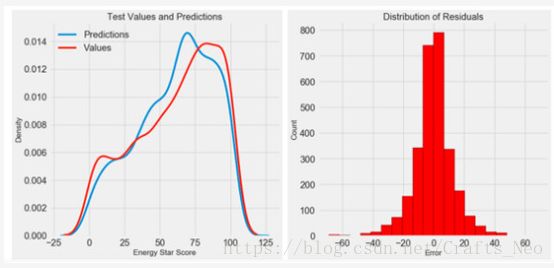
一旦我们有了最终的预测值,我们就可以看看他们是否表现出明显的偏差。左边是预测值和实际值的密度图,右边是残差的直方图:
模型预测似乎遵循实际值的分布,尽管密度的峰值出现在训练集的中值(66)附近,而非密度的真实峰值(接近100)。 残差几乎是正态分布。
2.8总结
介绍了机器学习工作流程中的几个步骤:
• 缺失值的插补和特征的缩放
• 评估和比较几种机器学习模型
• 使用随机网格搜索和交叉验证进行超参数调整
• 评估测试集上的最佳模型
这项工作的结果表明,机器学习适用于我们的任务(使用可用数据预测建筑物的Energy Star Score)。使用梯度增强回归法,我们可以预测测试集的分数在真实值的9.1分以内。 此外,我们还看到,超参数的调优可以提高模型的性能,但是需要相当大的时间成本。这是我们在开发机器学习解决方案时必须考虑的众多权衡之一。
三、模型解释与结果分析
Interpretinga machine learning model and presenting results
机器学习模型经常被批评是技术黑箱:只要输入数据就能得到正确答案,但却无法对其进行解释,在本系列的第三部分,作者展示一个完整的机器学习解决方案,并试图解释模型。
3.1 模型理解
模型由数百个决策树组成,通过梯度增强了回归的效果,虽然每个决策树都是可解释的,但这仍然是一个复杂的模型。我们将通过三种方式来了解我们的模型是如何预测的。
1、特征重要性【4】
2、单一决策树可视化
3、 LIME:Local Interpretable Model-AgnosticExplainations【5】
前两种方法是决策树特有的,而第三种方法可以广泛应用于任何机器学习模型。LIME是一个相对较新的包,目的是对机器学习预测进行解释【6】。
3.2 特征重要性
特征重要性分析是为了显示特征与预测目标任务的相关性。特征的重要性分析过程是相当复杂的,但我们可以使用相对值来比较哪些特征是最相关的,使用Scikit-Learn,可以从任意基于树结构的学习器中分析出特征的重要性程度。
我们的训练模型,可以使用model.feature_importances_方法来找出关键特征。并且可以将他们输入到pandas的数据帧中,并将前十位的关键特征显示出来。
可以看出,EUI(能量使用强度)和归一化的天气电力强度( Weather Normalized Site Electricity Intensity)是最重要的特征,占到重要性66%以上。从第三位特征开始,重要性明显下降,这表明我们并不需要使用所有的特征来获得更高效能。基于这些结果,我们可以回答最初的问题,建筑星级能源评分的最重要指标是EUI和归一化的天气电力强度。当我们想要读取更多的关键特征时【7】,这是种方法非常的有效,可以帮我们理解模型是如何运作的。
3.3 单一决策树的可视化
整个梯度增强回归器可能非常难以理解,但独立的决策树都非常的简单,我们可以使用Scikit-Learn函数export_graphviz【8】来可视化森林中的任意一棵决策树。
即使这棵树只有6层,但是也很难看清。 我们可以将调用修改为export_graphviz并将我们的树限制在更合理的两层
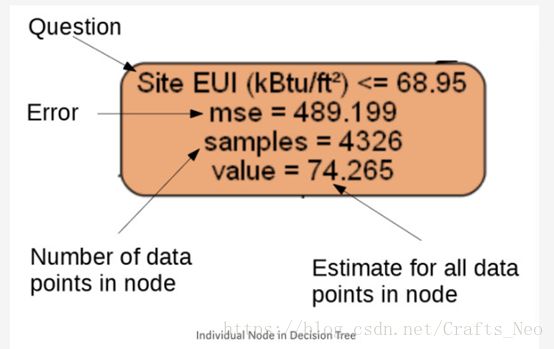
树中的每个节点都有四个属性信息:
1、一个数值判断表达式,来决定接下来该向左还是向右走
2、 Mse代表了节点的误差
3、 Samples表示样本数量
4、 Value表示节点中所有样例的估计值
(叶子节点只有2-4个,因为这代表了最终的估计值,并且没有任何的孩子节点。)
决策树通过从根节点对数据进行预测,逐渐遍历树中各个层次。例如,上述节点问题是:该建筑是否有一个小于或等于68.95的站点EUI?如果答案是肯定的,那么将进入右子节点,否则将进入左子节点。
这个过程在树中的每一层进行重复,直到叶子节点。随着树的深度增加,训练集上的误差都会减小,因为有更多的叶子节点,可以有助于更细粒度的划分,然而,层数太深将导致训练数据不够,而无法将预测能力推广到训练数据中。
在第二部分,我们对一些模型超参数进行了优化,这些模型控制了每棵树的各个方面,比如树的最大深度,和叶子节点所需的最小样本数量。这两点都对过拟合有巨大影响。对此,我们可以使用可视化工具展示出决策树的配置过程。
虽然我们无法对模型的每颗树都检查一遍,但可以了解每个独立决策树是如何作出预测的,这种基于流程图的方法看起来更像是一个人在做决定的方式:一次只回答一个问题。基于决策树的集合,整合了许多决策树的预测能力,创建了一个方差较小的精准模型。决策树的组合往往非常准确,而且很容易做出解释。
3.4 LIME(Local Interpretable Model-Agnostic Explanations)
最后一个工具(LIME)将帮助我们理解模型是如何思考的。LIME目标是解释任意独立的机器学习模型,方法是创建一个模型局部近似的模型,如线性回归等。
这里我们将使用LIME来考察模型预测错误的例子,以分析为什么模型会出错。首先,需要找出模型预测错误的样例,这可以通过训练与预测模型来提取。
接下来,我们创建LIME解释器扫描训练数据、模型、训练标签以及数据特征的名称。最后,通过解释器对错误预测作解释,扫描观测以及预测函数。
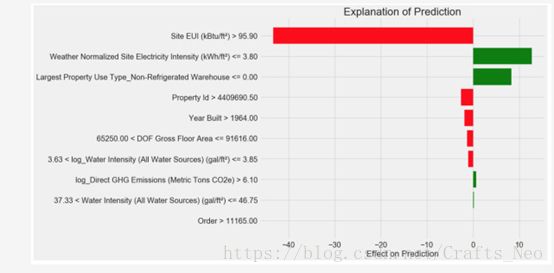
结果如图所示
图片解释如下:y轴的每个记录展示了该特征对预测结果的影响,红色和绿色的柱状图表示每个特征对预测的影响。例如,最上面的记录表示EUI高于95.90,为预测带来了40分的负向影响。第二条记录表示电力强度低于3.8,为模型预测带来了10分的正向影响,最终预测是一个截距项加上每一个单独的贡献之和。
也可以通过另一个解释器(.show_in_notebook())得出相似的结论。
# Show the explanation in the Jupyter Notebook
exp.show_in_notebook()
左边的结果展示了各个特征值对预测的贡献程度,右边的表中展示了数据变量的真实值。这个例子中,模型预测结果为12,而真实值是100!最初的结果可能是令人费解的,但看着这个解释,我们可以发现这是一个合理的估计。Site EUI的值比较高,我们预计能量分数会很低(因为EUI与分数的关系非常强),我们的模型也给出了这个结论,在这种情况下,逻辑是错误的,因为该建筑的真实分数是100分。
当一个模型错误时,可能会非常令人沮丧,但是这种方法,能够帮助我们理解为什么模型是错误的。此外,基于这一解释,我们可以探究为什么这座建筑会有这样的分数。也可以从中学到些新的东西,这种工具可能并不完美,但可以帮助我们理解模型,从而帮助我们做出更好的决策。
3.5 记录工作与结果报告
技术项目经常会忽视文档和报告。即使可以做很好的分析,但是如果无法清楚的表达结果,那么就不会有任何影响!
当我们记录一个数据科学项目时,可以获取所有的数据和代码,这样项目就可以被其他的数据科学家重现。重要的是,代码比文档要更常用得多,我们应该保证他人可以清楚的理解我们的工作。这意味着在代码中加入有用的注释并解释推理过程将非常有意义。我发现Jupyter笔记本是一个很好的文档工具,因为它们可以一步一步的输入注释和代码。
Jupyter笔记本也是一个分享信息的好平台。使用Jupyter,我们可以将代码隐藏在最终报告中,因为并不是每个人都想在文档中看到一堆Python代码!
本项目的最终结果:
1、 利用纽约能源数据,可以建立一个误差在9.1以内的模型,来预测建筑物的能源星级。
2、 EUI和电力强度是预测分数的最相关因素。
3.6 总结
我们完成了一个完整的端到端的机器学习项目,通过数据清洗、模型建立,最后看到了如何解释一个机器学习模型。机器学习项目的总体结构如下:
1、数据清洗和格式
2、探索性数据分析
3、工程特性和选择
4、比较机器学习模型和性能指标
5、对最佳模型进行超参数调优
6、评估测试集上的最佳模型
7、解释模型的结果
8、得出结论,并完成报告
虽然具体步骤因项目而异,机器学习通常是一个迭代过程,而不是线性的过程,希望以后在完成机器学习的项目中,借鉴该项目的整体思路,在机器学习的道路上披荆斩棘,愈挫愈勇!
原文链接:
https://towardsdatascience.com/a-complete-machine-learning-walk-through-in-python-part-three-388834e8804b
代码链接:
https://github.com/WillKoehrsen/machine-learning-project-walkthrough/blob/master/Machine%20Learning%20Project%20Part%203.ipynb