Coursera上Andrew Ng机器学习课程总结(一)
利用大约一个月的时间把coursera公开课Andrew Ng讲授的机器学习课程看完了,并且把8个编程联系也实现了,写篇总结来归纳下知识点。客观的来说,这门公开课很偏工程,老师对于数学知识能省则省,对于那些想初窥机器学习的同学,倒是很推荐看下。
机器学习按照训练集有无标签分为监督学习和无监督学习。监督学习,我们经常用它处理回归问题、分类问题,而课程里介绍的有:线性回归模型、logistics回归模型、神经网络及SVM模型;无监督学习,主要处理聚类的问题,课程里主要介绍的是K-means模型。
线性回归
线性回归问题,简单来说就是给出训练集,用线性函数来拟合这些数据,最后这个线性函数来计算给定自变量对应的因变量的值。
单变量的线性回归
我们的假设函数是 hθ(x)=θTx=θ0+θ1x1
为了使我们的假设函数能够更好的拟合训练集的数据,我们使用最小二乘法来定义代价函数
那么下面我们就需要极小化公式[1]
这里我们采用的方法即是梯度下降法(又叫做批量梯度法),给定一个学习速率或者说是步长 α ,不断更新 θ ,具体公式如下:
为了能够使梯度下降法每次迭代,代价函数都能够减少,我们往往会画图来观察代价函数值是否每次都在减少。我们上面说的 α ,当我们设定这个值比较小的时候,梯度下降很慢才收敛,但是这个值很大,那么很可能我们的代价函数反而是增加的。
多变量的线性回归
特征向量标准化
之所以要进行特征向量的标准化,是因为各个特征变量的值往往差距比较大,在进行梯度下降法的时候,速度慢。一般而言,我们标准化是特征值减去特征向量的均值最后在除以特征向量的标准差。
多变量线性回归
在梯度下降时,每个 θ 的分量要同步更新,即在一次迭代过程中,不能更新完了 θ1 ,再用新的 θ1 更新 θ2 。
梯度下降法,有时候需要做特征向量的标准化,是不是感觉有些麻烦,那么下面介绍的方法就不需要做这样的数据预处理工作了,它就是标准公式法:
Logistics回归
对于分类问题而言,假如使用线性回归模型,那么很可能存在噪声数据,导致我们的假设函数非常倾斜,那么就容易把正类判断为负类。
Logistics回归模型
want 0≤hθ(x)≤1 ,假设函数如下:
where function g is the sigmoid function
z=θTx ,我们称z函数为决策边界,当z>0时,那么[3]的值就会大于0.5,反之,小于等于0.5。
当我们预测的时候,假如[3]的值大于0.5,那我们就可以认为预测值是正类,反之,负类。
定义代价函数如下:
代价函数对 θ 求导公式如下:
正则化Logistics回归
对训练集的数据进行拟合,欠拟合(Underfitting),称作高偏差(high bias),过拟合(Overfitting),称作高方差(high variance)。我们使用正则化来减少过拟合。
对于公式[4],正则化话后公式变为:
同样的,对 θ 求导后公式[5]变为
当j=0时,
当 j≥1 时,
注意:我们通常不正则化 θ0 。当过拟合的时候,我们可以通过增加 λ 来减少前面的 θ 的值。
多类分类器
我们使用one-vs-all分类方法来进行多类的模型建立:先把1个类看做正类,把剩下的类看做负类,按照这个方法,分别对这些多类建立logistics回归模型,预测的时候把特征值分别带入到这些训练好的logistics函数里,预测的类别就是函数输出的最大概率值。
神经网络
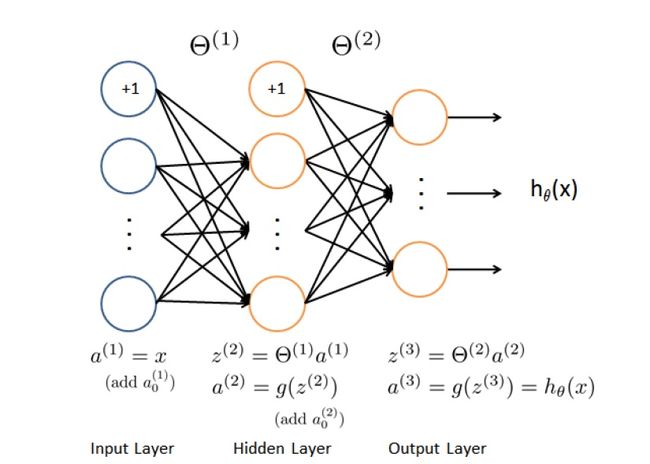
上图的模型是比较简单的。基本上一个神经网络要包括一个输入层(Input Layer)、一个输出层(Output Layer)及K个隐藏层(Hidden layer)。
正向传播
代价函数如下:
注意:这里的大K的值是输出层的数量,即最后的分类类别数量。
当我们使用神经网络时,很重要的是随机初始化每层的 θ ,防止对称性破缺。
反向传播
我们使用反向传播算法来计算神经网络的代价函数的导数。(为什么不再正向传播来计算?)
反向传播算法
假设训练集为 (x1,y1),...,(x(m),y(m))
设置 Δ(l)ij=0 ,其中l为层,i为l-1层的节点,j为l层的节点
For i=1 to m
Set a(i)=x(i)
Perform forward propagation to compute a(l) for l=2,3,…,L
Using y(i) ,compute δ(L)=a(L)−y(i)
Compute δ(L−1),δ(L−2),...,δ(2)
Δij(l):=Δij(l)+a(l)jδ(l+1)i
————————————————————————————————
Dij(l):=1mΔ(l)ij+λΘ(l)ij if j<>0
Dij(l):=1mΔ(l)ij if j=0
∂∂Θ(l)ijJ(Θ)=Dij(l)
训练模型评价
通常我们把样本集按照6:2:2的比例分为:训练集、验证集和测试集。
只介绍两种作图分析方法:
lambda曲线
正则化后,横轴为 λ ,纵轴为不带正则化的代价函数,通过绘制训练集和验证集来分析高偏差和高方差情况。
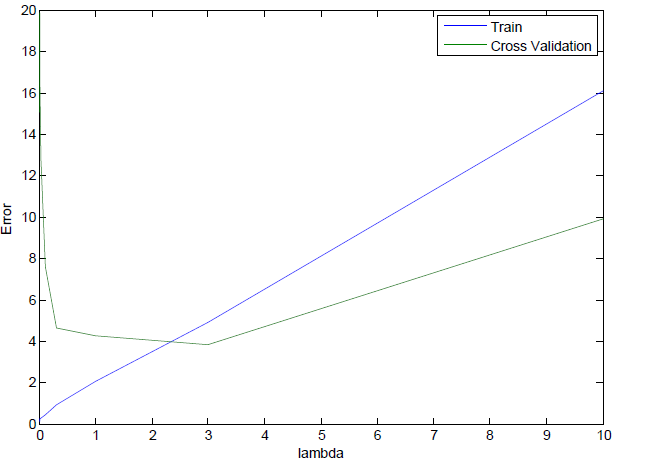
从上图可以看到,随着 λ 增加,训练集(蓝线)从高方差到高偏差,而验证集(绿色)从高方差-低方差-高偏差。
学习曲线
横轴为样本数量m,纵轴为不带正则化的代价函数,同样的需要绘制训练集和验证集来分析高偏差和高方差情况。
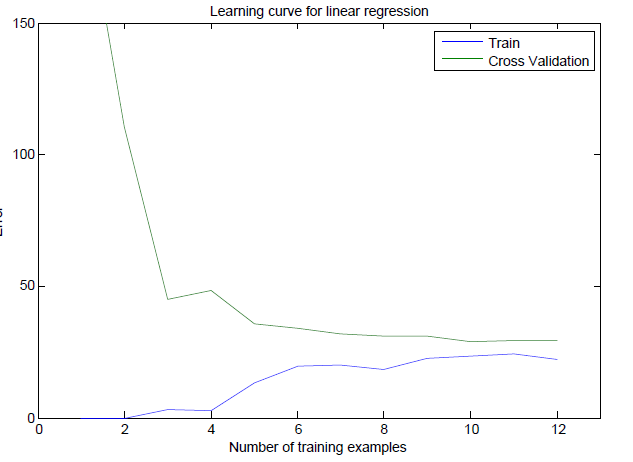
上图是高偏差情况,随着样本数量的增加,训练集和验证集趋于稳定并且相差不大。这种情况,盲目的增加样本数量是起不来作用的(想想为什么)。

上图是高方差的情况,随着样本数量的增加,训练集和验证集趋于稳定但是相差较大。这种情况,增加样本数量是能够减少误差。
单值分析
通常我们把y=1的标签给那些不常出现的类,即偏斜类。为了能用单值衡量我们系统的优劣,我们引入F值,再讲F值之前,我们先看下什么是查准率和召回率。
设tp=正类and预测为正类的数量,
fp=负类and预测为正类的数量,
fn=正类and预测为负类的数量。
查准率 P=tp/(tp+fp)
召回率 R=tp/(tp+fn)
一个系统P值和R值不可能同时很大。举个例子,logistics回归,我们把0.5阀值设置的大点,改为0.7,那么tp减少,fp减少,fn增大,那我们的P增大,R减小,也就是说我们预测的更准确了。反之,R高,P低。
通常我们使用它们的调和平均数来衡量,即F = 2(P*R)/(P+R) , F值大,较好。
支持向量机
支持向量机(support vector machine),简称SVM。
不打算按照公开课的思路来讲,发个牛人写的SVM三境界支持向量机通俗导论
我只来整理下公开课上logistics回归和SVM的使用情形。
设n为特征向量,m为训练集样本量
当n相对于m很大时,比如n=10000,m=10-1000。使用logistics回归或者是不带核函数的SVM。
当n很小,m中等程度时,比如n=1-1000,m=10-10000。使用带高斯核函数的SVM。
当n很小,m很大时,比如n=1-1000,m=50000以上。增加更多的特征量,然后使用logistics回归或者不带核函数的SVM。