机器学习笔记一：概述

机器学习的公认定义[Mitchell, 1997]：

A computer program is said to learn from experience E with respect to some class of tasks T and performance measure P if its performance at tasks in T, as measured by P, improves with experience E.

基本概念

机器学习领域常用的术语有，数据集(data set)，可以细分为训练集(training set)，验证集(validation set)和测试集(test set)。单条记录称为实例(instance)或者样本(sample)，其中包含特征(feature)和标签(label)，特征张成的空间称为特征空间或者样本空间(sample space)，一个样本往往由一个特征向量(feature vector)表示。学得模型对应了关于数据的某种潜在规律，称为假设(hypothesis)，这种潜在规律自身，称为真相(ground-truth)。学得模型适用于新样本的能力，称为泛化(generalization)能力。所有的机器学习模型都基于这样的基本假设：样本空间中全体样本服从一个未知分布(distribution) D D ，获得的每个样本都是独立地从这个分布上采样获得的，即独立同分布(independent and identically distributed, 简称 i.i.d. i . i . d . )。

学习过程可以看作是一个在所有假设(hypothesis)组成的假设空间(hypothesis space)中进行搜索的过程，搜索目标是找到与训练集匹配(fit)的假设，假设的表示一旦确定，假设空间及其规模大小就确定了。现实问题中，假设空间会很大，但学习过程是基于有限样本训练集进行的，因此可能有多个假设与训练集一直，即存在着一个与训练集匹配的“假设集合”，称之为版本空间(version space)，如何判定哪一个更好，需要根据归纳偏好(inductive bias)选择。归纳偏好对应了学习算法本身所做出的关于“什么样的模型更好”的假设。在具体的现实问题中，这个假设是否成立，即算法的归纳偏好是否与问题本身匹配，大多数时候直接决定了算法能否取得好的性能。最常用的原则是奥卡姆剃刀原则(Occam’s razor)，若有多个假设与观察一致，则选最简单的那个。

但是，没有免费的午餐定理(No Free Lunch Theorem，简称NFL)，告诉我们好不是绝对的，若学习算法 La L a 在某些问题上比学习算法 Lb L b 要好，则必然存在另一些问题，在这些问题中 Lb L b 比 La L a 表现更好，这个结论对任何算法均成立，证明简述为任意两个算法的期望性能相等：

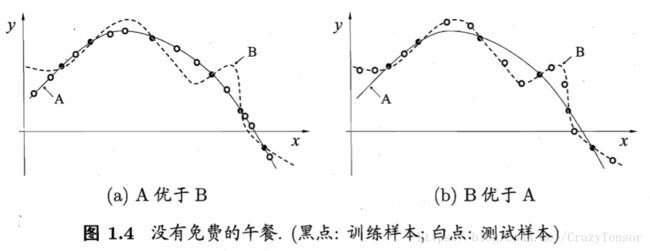
NFL定理最重要的寓意，是让我们清楚地认识到，脱离具体问题，空谈“什么学习算法更好”毫无意义，因为若考虑所有潜在的问题，则所有学习算法都一样好。要谈论算法的相对优劣，必须要针对具体的学习问题；在某些问题上表现好的学习算法，在另一些问题上却可能不尽如人意，学习算法自身的归纳偏好与问题是否相配，往往会起到决定性的作用。

统计学习三要素

统计学习方法(statistical learning)是关于计算机基于数据构建概率统计模型并运用模型对数据进行预测与分析的一门学科。统计学习对象是数据(data)，关于数据的基本假设是同类数据具有一定的统计规律性。对数据的预测与分析是通过构建概率统计模型实现的。

统计学习由监督学习(supervised learning)、非监督学习(unsupervised learning)、半监督学习(semi-supervised learning)和强化学习(reinforcement learning)等组成。监督学习的方法概括如下：从给定的、有限的、用于学习的训练数据集合出发，假设数据是独立同分布产生的，应用某个评价准则(evaluation criterion)，从假设空间中选取一个最优的模型，使它对已知训练数据及未知测试集数据在给定的评价准则下有最优的预测，最优模型的选取由算法实现。

统计学习方法包括模型的假设空间、模型选择的准则以及模型学习的算法，称其为统计学习方法的三要素，简称为模型(model)、策略(strategy)和算法(algorithm)：

方法 = 模型 + 策略 + 算法

模型

假设空间 F F 通常由一个参数向量决定的函数族：

F={f|Y=fθ(X),θ∈Rn} F = { f | Y = f θ ( X ) , θ ∈ R n }

参数向量 θ θ 取值于 n n 维欧式空间 Rn R n ，称为 参数空间(parameter space)。

策略

有了模型的假设空间，需要使用策略从中选取最优假设。
损失函数(loss function)：度量模型一次预测的好坏。常用损失函数有以下几种：

• 0-1 损失函数(0-1 loss function)
  
  L(Y,f(X))={1,0,Y≠f(X)Y=f(X) L ( Y , f ( X ) ) = { 1 , Y ≠ f ( X ) 0 , Y = f ( X )
• 平方损失函数(quadratic loss function)
  
  L(Y,f(X))=(Y−f(X))2 L ( Y , f ( X ) ) = ( Y − f ( X ) ) 2
• 绝对损失函数(absolute loss function)
  
  L(Y,f(X))=|Y−f(X)| L ( Y , f ( X ) ) = | Y − f ( X ) |
• 对数似然损失函数(log-likelihood loss function)
  
  L(Y,f(X))=−logP(Y|X) L ( Y , f ( X ) ) = − l o g P ( Y | X )

风险函数(risk function)或期望损失(expected loss)，模型 f(X) f ( X ) 关于联合分布 P(X,Y) P ( X , Y ) 的平均意义下的损失：

Rexp(f)=Ep[L(Y,f(X))] R e x p ( f ) = E p [ L ( Y , f ( X ) ) ]

学习的目的就是选择期望风险最小的模型，但是显然 P(X,Y) P ( X , Y ) 是未知的， Rexp(f)=Ep[L(Y,f(X))] R e x p ( f ) = E p [ L ( Y , f ( X ) ) ] 不可求。

经验风险(empirical risk)或者经验损失(empirical risk)，模型 f(X) f ( X ) 关于训练集的平均损失：

Remp(f)=1N∑i=1NL(yi,f(xi)) R e m p ( f ) = 1 N ∑ i = 1 N L ( y i , f ( x i ) )

根据大数定理，当样本容量 N N 趋于无穷时，经验风险 Remp(f) R e m p ( f ) 趋于期望风险 Rexp(f) R e x p ( f ) 。但是现实中训练样本数量有限，用经验风险估计期望风险常常不理想，需要矫正，所以监督学习有两个基本策略：

• 经验风险最小化(empirical risk minimization, ERM)，样本容量足够时，能保证很好的效果，不然会出现过拟合(over-fitting)现象：
  
  minf∈F1N∑i=1NL(yi,f(xi)) min f ∈ F 1 N ∑ i = 1 N L ( y i , f ( x i ) )
  
  例子：极大似然估计(maximum likelihood estimation)，当模型是条件概率分布，损失函数是对数似然损失函数，经验风险最小化就等价于极大似然估计。
• 结构风险最小化(structural risk minimization，SRM)，为了防止过拟合而提出来的策略。结构风险最小化等价于正则化(regularization)，在经验风险上加上表示模型复杂度的正则化项(regularizer)或惩罚项(penalty term)：
  
  minf∈FRsrm(f)=minf∈F1N∑i=1NL(yi,f(xi))+λJ(f) min f ∈ F R s r m ( f ) = min f ∈ F 1 N ∑ i = 1 N L ( y i , f ( x i ) ) + λ J ( f )
  
  其中 J(f) J ( f ) 表示模型复杂度，是定义在假设空间 F F 上的泛函。 λ≥0 λ ≥ 0 是正则化系数，用于权衡经验风险和模型复杂度，结构风险小需要两者都小，这样的模型往往对训练数据以及未知的测试数据都有较好的预测。
  例子：最大后验概率估计(maximum posterior probability, MAP)，当模型是条件概率分布，损失函数是对数似然损失函数，模型复杂度由模型的先验概率表示，结构风险最小化就等价于最大后验概率估计。

算法

前面的策略都认为对应风险最小的模型是最优模型，所以监督学习问题就变成了经验风险或结构风险函数最优化问题。统计学习的算法就是求解最优化问题的优化算法。极少一部分最优化问题有显式的解析解，但是大部分需要用数值计算的方法求解，比如梯度下降算法。

发展历程

未完待续…