【平衡二叉树】SBT学习笔记
醒目：文章部分内容来源于网络上的资料，感谢xkey（http://blog.csdn.net/acceptedxukai ）、百度百科、神的不在场证明（http://www.cnblogs.com/zgmf_x20a/）感谢网络上提供各种资料的神犇们
概述
SBT，即Size Balanced Tree，节点大小平衡树，是一种自平衡二叉查找树，是在计算机科学中用到的一种数据结构。它是由中国广东中山纪念中学的陈启峰发明的。实践中，SBT是所有种类的平衡树中效率较高的一种。SBT的高度是O(logn)，Maintain是O(1)，所有主要操作都是O(logn)。SBT的特点是，它需要专门去维护其大小，从而实现构建平衡二叉树的目的。
Size Balanced Tree(简称SBT)是一种平衡二叉搜索树，它通过子树的大小s[t]来维持平衡性质。它支持很多动态操作，并且都能够在O(log n)的时间内完成。
| Insert(t,v) |
将键值为v的结点插入到根为t的树中 |
| Delete(t,v) |
在根为t的树中删除键值为v的结点 |
| Find(t,v) |
在根为t的树中查找键值为v的结点 |
| Rank(t,v) |
返回根为t的树中键值v的排名。也就是树中键值比v小的结点数+1 |
| Select(t,k) |
返回根为t的树中排名为k的结点。同时该操作能够实现Get-min,Get-max,因为Get-min等于Select(t,1),Get-max等于Select(t,s[t]) |
| Pred(t,v) |
返回根为t的树中比v小的最大的键值 |
| Succ(t,v) |
返回根为t的树中比v大的最小的键值 |
SBT定义
struct SBT
{
int key,left,right,size;
} tree[N];其中，data是节点数值，left/right左右子树，size是节点的大小
显而易见，作为平衡树，SBT有一种性质，即某子树的大小大于等于其兄弟子树的大小。
关于这一点的代码体现：
tree[i].left.size >= max(tree[i].right.right.size, tree[i].right.left.size) tree[i].right.size >= max(tree[i].left.left.size, tree[i].left.right.size) 左旋和右旋
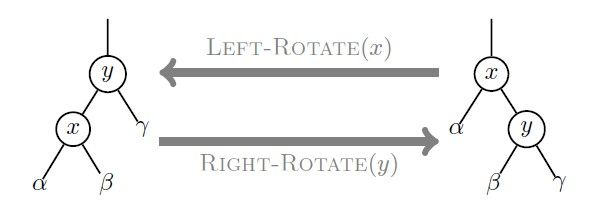
二叉左旋
一棵二叉平衡树的子树，根是Root，左子树是x，右子树的根为RootR，右子树的两个孩子树分别为RLeftChild和RRightChild。则左旋后，该子树的根为RootR，右子树为RRightChild，左子树的根为Root，Root的两个孩子树分别为x（左）和RLeftChild（右）。
二叉右旋
一棵二叉平衡树的子树，根是Root，右子树是x，左子树的根为RootL，左子树的两个孩子树分别为LLeftChild和LRightChild。则右旋后，该子树的根为RootL，左子树为LLeftChild，右子树的根为Root，Root的两个孩子树分别为LRightChild（左）和x（右）。
左子节点与右子节点对称的树就是平衡树，否则就是非平衡树。
非平衡树会影响树中数据的查询，插入和删除的效率。比如当一个
二叉树
极不平衡时，即所有的节点都在根的同一侧，此时树没有分支，就变成了一个
链表
。数据的排列是一维的，而不是二维的。在这种情况下，查找的速度下降到O(N)，而不是平衡二叉树的O(logN)。
为了能以较快的时间O(logN)来搜索一棵树，需要保证树总是平衡的（或者至少大部分是平衡的）。这就是说对树中的每个节点在它左边的后代数目和在它右边的后代数目应该大致相等。
代码实现
void left_rot(int &x)
{
int y = tree[x].right;
tree[x].right = tree[y].left;
tree[y].left = x;
tree[y].size = tree[x].size;//转上去的节点数量为先前此处节点的size
tree[x].size = tree[tree[x].left].size + tree[tree[x].right].size + 1;
x = y;
}void right_rot(int &x)
{
int y = tree[x].left;
tree[x].left = tree[y].right;
tree[y].right = x;
tree[y].size = tree[x].size;
tree[x].size = tree[tree[x].left].size + tree[tree[x].right].size + 1;
x = y;
}Maintain函数
当我们在平衡树中插入一个新的点时，会破坏这棵树的平衡性，这时我们就需要调用一个Maintain函数对树进行修改直到它重新变回平衡树。我们定义Maintain(T)为修复以T为根节点的平衡树，则很显然的，调用Maintain(T)的前提条件是，T的左右子树都已经是平衡树了。
插入节点时，我们一共需要考虑四种情况
分别是
1.x.left.left.size > x.right.size
2.x.left.right.size > x.right.size
3.x.right.right.size > x.left.size
4.x.right.left.size > x.left.size
但是由于SBT的两条性质是互相对称的，所以这里只列举其中两种情况的操作。
1.x.left.left.size > x.right.size
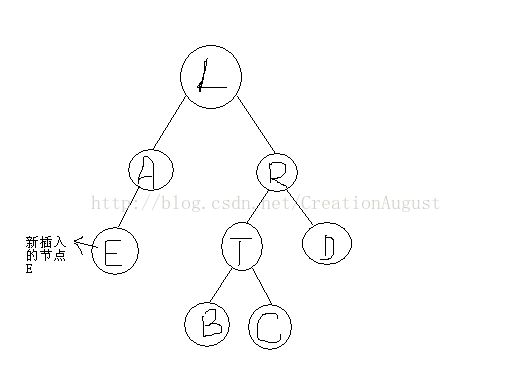
在原本平衡的状态下，当我们进行insert(T.left,data)后，如果A.size>R.size
则进行如下操作：
1、首先执行Right-Ratote(t)，这个操作使上图变成下图：
2.如果进行右旋操作后，这棵树仍然不是一颗平衡树，即存在C.size>B.size||D.size>B.size，那么就需要再一次调用Maintain(T)对T进行调整
3.调整后，L的右子树被连续调整，导致整棵树右偏，这时候就需要再次进行校正，直到整棵树平衡为止
（此处没有图片，根据自己理解画了一个调整后的图片，可能会有错误，希望神犇能够予以指出，不要让我的错误影响了别人）
（不要在意这张图的美观性）
2.x.left.right.size > x.right.size
在原本平衡的状态下，当我们进行insert(T.left,data)后，如果B.size > R.size
那么进行如下的操作
1、首先执行左旋操作Left-Ratote(L)后，就会变成下面的样子
2、接着执行一次右旋操作Right-Ratote(T)，变成下图：
3、在经过两个巨大的旋转之后，整棵树就变得非常不可预料了。万幸的是，子树A;E; F;R 依然是容均树，所以要依次修复L 和T，Maintain(L),Maintain(T)。（P.S.容均树就是情况1的第一张图，那就是一个标准容均树【不过大概所有人都知道吧=-=】）
4、子树都已经是容均树了，但B可能还有问题，所以还要调用Maintain(B)
第三种情况：x.right.right.size > x.left.size
与第一种情况相反
第四种情况：x.right.left.size > x.left.size
与第二种情况相反
Maintain函数的伪代码
Maintain (t,flag)
If flag=false then
If s[left[left[t]]>s[right[t]] then //case1
Right-Rotate(t)
Else
If s[right[left[t]]>s[right[t]] then //case2
Left-Rotate(left[t])
Right-Rotate(t)
Else //needn’t repair
Exit
Else
If s[right[right[t]]>s[left[t]] then //case1'
Left-Rotate(t)
Else
If s[left[right[t]]>s[left[t]] then //case2'
Right-Rotate(right[t])
Left-Rotate(t)
Else //needn’t repair
Exit
Maintain(left[t],false) //repair the left subtree
Maintain(right[t],true) //repair the right subtree
Maintain(t,false) //repair the whole tree
Maintain(t,true) //repair the whole treeMaintain函数的代码
void maintain(int &x,bool flag)
{
if(flag == false)//左边
{
if(tree[tree[tree[x].left].left].size > tree[tree[x].right].size)//左孩子的左子树大于右孩子
right_rot(x);
else if(tree[tree[tree[x].left].right].size > tree[tree[x].right].size)//右孩子的右子树大于右孩子
{
left_rot(tree[x].left);
right_rot(x);
}
else return;
}
else //右边
{
if(tree[tree[tree[x].right].right].size > tree[tree[x].left].size)//右孩子的右子树大于左孩子
left_rot(x);
else if(tree[tree[tree[x].right].left].size > tree[tree[x].left].size)//右孩子的左子树大于左孩子
{
right_rot(tree[x].right);
left_rot(x);
}
else return;
}
maintain(tree[x].left,false);
maintain(tree[x].right,true);
maintain(x,true);
maintain(x,false);
}插入操作
只需要在每次插入节点后加一个Maintain操作矫正一下平衡树就好了
void insert(int &x,int key)
{
if(x == 0)
{
x = ++top;
tree[x].left = tree[x].right = 0;
tree[x].size = 1;
tree[x].key = key;
}
else
{
tree[x].size ++;
if(key < tree[x].key) insert(tree[x].left,key);
else insert(tree[x].right,key);//相同元素插入到右子树中
maintain(x, key >= tree[x].key);//每次插入把平衡操作压入栈中
}
}寻找前驱
data为查找值x为当前访问的子树y为保存的前驱节点
if(tree[x].data< data) 则说明其前驱(小于data中所有元素最大的那个)在当前查找节点的右子树，并且设定当前节点x为其前驱
if(tree[x].data >= data)说明其前驱在当先查找节点的左子树，当前节点x的data值也不是其前驱，所以设定其前驱仍为y
int pred(int &x,int y,int key)//前驱 小于
{
if(x == 0) return y;
if(tree[x].key < key)//加上等号，就是小于等于
return pred(tree[x].right,x,key);
else return pred(tree[x].left,y,key);
}//pred(root,0,key)
寻找后继
与前驱类似
int succ(int &x,int y,int key)//后继 大于
{
if(x == 0) return y;
if(tree[x].key > key)
return succ(tree[x].left,x,key);
else return succ(tree[x].right,y,key);
}删除操作
与普通维护size域的BST删除相同。关于无需Maintain的说明by sqybi：
在删除之前，可以保证整棵树是一棵SBT。当删除之后，虽然不能保证这棵树还是SBT，但是这时整棵树的最大深度并没有改变，所以时间复杂度也不会增加。这时，Maintain就显得是多余的了。（这一大坨文字莫名的抽象，留着多琢磨一下才看得懂。。。）
下面给出两种删除方式，一种是找前驱替换，一种是找后继替换
后继替换
int remove(int &x,int key)
{
tree[x].size --;
if(key > tree[x].key)
remove(tree[x].right,key);
else if(key < tree[x].key)
remove(tree[x].left,key);
else
{
//有左子树，无右子树
if(tree[x].left != 0 && tree[x].right == 0)
{
int temp = x;
x = tree[x].left;
return temp;
}
else if(tree[x].right !=0 && tree[x].left == 0)
{
int temp = x;
x = tree[x].right;
return temp;
}
//无左子树和右子树
else if(!tree[x].left && !tree[x].right)
{
int temp = x;
x = 0;
return temp;
}
//有右子树
else //找到x右子树中最小元素，也就是找后继元素
{
int temp = tree[x].right;
while(tree[temp].left) temp = tree[temp].left;
tree[x].key = tree[temp].key;
//tree[x].cnt = tree[temp].cnt;
remove(tree[x].right,tree[temp].key);
}
}
}
前驱替换
int remove(int &x,int key)
{
int d_key;
//if(!x) return 0;
tree[x].size --;
if((key == tree[x].key)||(key < tree[x].key && tree[x].left == 0) ||
(key>tree[x].key && tree[x].right == 0))
{
d_key = tree[x].key;
if(tree[x].left && tree[x].right)
{
tree[x].key = remove(tree[x].left,tree[x].key+1);
}
else
{
x = tree[x].left + tree[x].right;
}
}
else if(key > tree[x].key)
d_key = remove(tree[x].right,key);
else if(key < tree[x].key)
d_key = remove(tree[x].left,key);
return d_key;
}寻找最小值
int getmin()
{
int x;
for(x = root ; tree[x].left; x = tree[x].left);
return tree[x].key;
}寻找最大值
int getmax()
{
int x;
for(x = root ; tree[x].right; x = tree[x].right);
return tree[x].key;
}寻找第K小的数
int select(int &x,int k)//求第k小数
{
int r = tree[tree[x].left].size + 1;
if(r == k) return tree[x].key;
else if(r < k) return select(tree[x].right,k - r);
else return select(tree[x].left,k);
}询问某元素在树中是第几大
int rank(int &x,int key)//求key排第几
{
if(key < tree[x].key)
return rank(tree[x].left,key);
else if(key > tree[x].key)
return rank(tree[x].right,key) + tree[tree[x].left].size + 1;
return tree[tree[x].left].size + 1;
}
引用原话：“如果我们在数据结构中加上一个字段cnt,专门用来记录重复数据的个数，这样的话树中就没有重复数据，因为它们已经被合并了，这里需要修改insert函数和remove函数和旋转操作，如果删除操作每次删除的是整个节点而不是cnt>2就仅仅将cnt--而是整个删除，这样就会对size造成很大的影响 ，这种情况的remove函数我暂时没有想好如何去写，首先可以确定思路，如果删除节点是x，它的直接或间接父亲节点的size都需要减去x.cnt，但是我们是用的替换删除，这里怎么操作？”
关于考虑重复元素的问题，我也在思考=-=等某年某月入过我会搞了我就把它挂出来www
至于为什么一开始学平衡树就选择SBT，因为似乎SBT和Treap的代码最简洁最好写，而且SBT更加易于理解来着？