二分匹配——匈牙利算法和KM算法
一、二分图
定义:若把简单图G的顶点集分成两个不相交的非空集合V1和V2,使得图中每一条边都连接V1中的一个顶点和V2中的一个顶点(边的两个端点一个在V1中,另一个在V2中),则图G称为二分图,此时称(V1,V2)为G的顶点集的一个二部划分。
什么是简单图?
定义:图G的每条边都连接两个不同的顶点,且没有两条相同的边连接同一对顶点,则图 G 称为简单图。(没有多重边,没有一个顶点自身形成一个环)
二、判断一个图是否是二分图
定理:一个简单图是二分 图,当且仅当能够对图中任意相邻的两点赋予两种不同的颜色,使得没有一对相邻的顶点被赋予相同的颜色。(一个顶点只可能是两种颜色中的一种)
三、什么是匹配
一个匹配即是二分图中一个包含若干条边的集合,且其中任意两条边没有公共端点。所以一个二分图的匹配可以有多个。
四、最大匹配和完美匹配
1、顾名思义,在一个二分图的所有匹配中,包含边数最多的一个匹配就是最大匹配。
说到最大匹配,就顺便说一下最小点覆盖。因为最大匹配数 = 最小点覆盖
点覆盖的定义:图G=(V,E)中的一个点覆盖是一个集合S⊆V使得每一条边至少有一个端点在S中。
最小点覆盖顾名思义就是含最少元素的 S。
下面给出 最大匹配数 = 最小点覆盖 的证明(参考了其他博主的想法再结合自己的想法)
①最小点覆盖 <= 最大匹配数
若最大匹配数为 n ,则存在n条不相邻的边。取每一条边的一个端点,组成一个点集S,则最小点覆盖至少需要包含 |S|个点。
②最大匹配数 >= 最小点覆盖
对于最小点覆盖集S中的任一点,总有一条边连接该点与集合外的一点。若不存在这样的边,则所有以该点为端点的边同时有连接了S中的其他点,这样的话即使把该点从S中删去,得到原图的一个更小的点覆盖,这与S是最小点覆盖矛盾。所以对S中任一点v,存在一条连接v和不属于S的点w的边。对S中每一个v,都取这样一条边,构成一个边集E。下面证明E中每一条边都不相邻。若存在相邻的两条边,则存在v1、v2属于S且与S外同一点w相邻。由E的构成方式可知,在不属于S的点中,只有w与v1相邻,也只有w与v2相邻。有二分图的性质可知,在所有点中只有w与v1相邻,只有w与v2相邻,所以将S中的v1,v2删去,将w加入到S中,我们可以得到一个对于原图来说更小的点覆盖,这与S是最小点覆盖矛盾,所以E中每一条边都不相邻。所以E构成的了原图的一个匹配,所以最大匹配数 >= 最小点覆盖。
综上,最小点覆盖 == 最大匹配数。
2、若二分图的一个匹配为M,其划分为(V1,V2),若V1中每个顶点都是M中边的端点,即 |M| = |V1| (M中的边数等于V1的顶点数),则该匹配称为完美匹配。
所以,完美匹配一定是最大匹配,最大匹配不一定是完美匹配;且一个二分图肯定有最大匹配,但不一定有完美匹配。
五、最优匹配
最优匹配又称为带权最大匹配,是指在带有权值边的二分图中,求一个匹配使得匹配边上的权值和最大。一般求最优匹配时,所求二分图的划分(V1,V2)的顶点数相同,使得每一个顶点都需要被匹配,这样也就等同求出了完美匹配。如果V1和V2的顶点数不同,可以通过补点加权值0边实现转化,然后用KM算法解决。
说了那么多概念,接下来开始说算法了!!!
一、匈牙利算法——求二分图最大匹配
算法步骤:从一个未匹配的顶点出发,依次经过非匹配边、匹配边、非匹配边…形成一条路径,按此路径走找到第一个不同于起点的未匹配点V,则不再走下去。把起点和V的路径上的未匹配边都换成匹配边,已匹配边都换成未匹配边。重复这样,直到找不到这样的路径。
为什么这样就能得到最大匹配?
因为我们寻找的路径的起点和终点都是未匹配的点,且路径上的边是交替的,即是一条已经匹配的边和一条还未匹配的边交替存在。这样的话,这条路径上的未匹配边肯定比已经匹配的边多一(不清楚的话可以手动画一下)。将未匹配的边换成已经匹配的边,已经匹配的边换成未匹配的边,这样的话就形成一个比原匹配多一条边的匹配。当找不到这样一条路径时,我们就已经找到最大匹配了。
上述的路径称为增广路径。
这是我学习匈牙利算法时参考的博客,里面有图解
下面是匈牙利算法的DFS实现:
其中图的表示是用邻接表表示;我把算法封装成一个结构体
#includeint v = adj[u][i];
if(!vis[v])
{
vis[v] = 1;
//分两种情况讨论:
//1、找到可以和u匹配的未匹配的点v,因为u和v都未匹配,所以把连接u和v的边加入匹配中,可以得到更大的匹配。
//2、如果与u相连的点v已经匹配好了,那么从v的匹配点开始搜索。
//因为我们要寻找一条交替的路径,由于u为匹配,所以任何以u为端
//点的边都是未匹配的边,从u开始寻找路径,找的第一条边就是未匹
//配的,如果该边的另一个端点已经匹配,就继续从它所匹配的点开始
//寻找路径,这样的话我们的路径上的第二条边就是v到它所匹配的点
//的边,该边是已经匹配的边,这就是匈牙利算法的思想了。
if(!mat[v]||path(mat[v]))
{
//标记对应的匹配
mat[v] = u;
mat[u] = v;
//成功找到增广路
return 1;
}
}
}
//无增广路,已经达到最大匹配
return 0;
}
int Match()
{
//最小点覆盖数
int min_point_cover = 0;
依次遍历所有的点,若已知二分图的划分(V1,V2),则遍历其中一个点集的点即可
for(int i=1;i<=num;++i)
{
//每一次寻找增广路时顶点不能重复访问
vis.assign(n+1,0);
//以未匹配点为起点,若有增广路则最小点覆盖加一,因为匹配每一个都是多一条边
if(!mat[i]&&path(i))
min_point_cover ++;
}
return min_point_cover;
}
}; 二、KM算法——求二分图的最佳匹配(运用匈牙利算法辅助求解)
这是一个很好的学习KM算法的博客,我就是通过这个学习的
我的理解是:
先忽略所有的边,把原图看成一张新的图,其中的顶点不变,然后往新图中添加边,保证每一次添加边后新图的边的总权值在满足匹配的条件下是最大的,不断加边,直到得到最佳匹配。
首先明确二分图的划分(左,右),将左边第一个点的权值最大的边加入新图,然后搜索左边点集的第二个点,把和它相连的权值最大的边(w)加入新图,如果 w 的另一个端点已经匹配,那么我们要为新图重新分配边,为了保证重新分配的边的总权值和把 w 加入新图得到的总权值的差最小(保证了最佳匹配的取得),我们依次把已经在新图里的边,跟左边的已经匹配好的点的其他未匹配的邻边比较,让权值相差最小的那两条边交换,即若A和B两条边权值相差最小,A在新图中而B不在,那么用B代替A,这样我们把新图的边重新分配,使得可以满足匹配的条件的同时所有边的总权值最大。(如果把上述 的w添加进新图,那形成的就不是匹配啦)。
依据这种思路,最终得到最佳匹配。这种思路很像匈牙利算法寻找增广路的思路,其实我觉得同理,我们要为左边还未匹配的点寻找适合的匹配,这个匹配要满足的是,添加这个匹配边后已形成的匹配的总权值要最大。所以只是在匈牙利算法寻找增广路上加一些限制。
看代码前需要了解:
KM算法引入了一种表示边的方式:顶标(用数组表示,T[i]=5表示 i 点的顶标为5)
一开始把左边的点的顶标初始化为跟该点相连的边的最大权值,右边的点的顶标初始化为0。 T[左] + T[右] = G[左][右](G为邻接矩阵) 表示边 G[左][右]可以选择添加进新图。
此处借用上述博客中的一张图说明:
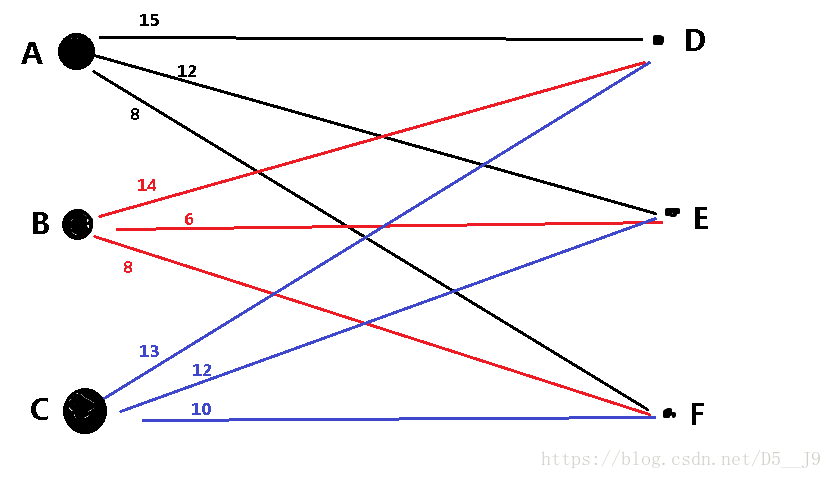
初始化后,A的标杆为15,B的标杆为14,C的标杆为13;而D、E、F的标杆都为0。
算法流程:
1、初始化可行顶标的值
2、用匈牙利算法判断是否有符合条件的增广路,
3、若未找到符合的增广路则修改可行顶标的值(换边)
4、重复(2)(3)直到找到最佳匹配为止
代码如下:
此代码是题解代码,原题为HDU2255
其中一些针对于题目的表示我已经注释明白,可以当成算法模板看。
需要注意的是这种实现方式不是最优化的KM算法,等以后学习了我再整理成博客。
#include没想到这篇博客写了三个多小时。。。
若有不足的地方等发现后再修改,夜已深,先入睡。
感叹一点,在写博客的时候不仅对学过的知识回顾复习,而且还不时有新的理解。真是温故而知新!