梯度下降法实现线性回归（python手动实现+Tensorflow实现）

ps: 此专题为AI领域经典算法书籍及论文解析与代码复现，AI算法讲解。欢迎关注知乎专栏《致敬图灵》
https://www.zhihu.com/people/li-zhi-hao-32-6/columns
微信公众号：‘致敬图灵’。

1.梯度下降法介绍

1.1梯度

梯度是指一个多元函数，对每一个参数求偏导，所得到的向量就是梯度。
eg：
$$▽f(x1,x2,x3...xn)=(\frac{\partial y}{\partial x1},\frac{\partial y}{\partial x2},\frac{\partial y}{\partial x3}...\frac{\partial y}{\partial xn})$$
上述相当于标量函数对向量变量进行求导，所得到得即时梯度，而多是高维函数对高位变量进行求导，得到的则是雅可比矩阵。

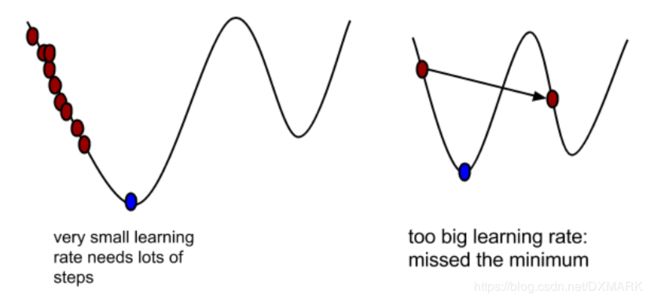
1.2梯度下降法

梯度下降法，简单来说，就是以一定的学习率$a$，或者说是步长，从当前位置，向梯度方向$(\frac{\partial y}{\partial x1},\frac{\partial y}{\partial x2},\frac{\partial y}{\partial x3}...\frac{\partial y}{\partial xn})$下降。

从数学公式上来看：$(x1,x2,x3...xn)-a\ast ▽f(x1,x2,x3...xn)$,即进行了一次梯度下降。

其中学习率为$a$，这个参数是十分重要的，若$a$太小，则迭代次数很多，下降缓慢，若$a$过大，则无法达到最低点。

此种方法用于获得模型的参数。

建模的步骤一般如下：

1. 获取观测数据（即我们手中现有的数据）
2. 确定模型与参数
3. 对参数进行估计（下面梯度下降法开始发挥它的用处）
4. 确定损失函数
5. 通过损失函数对参数进行求导，得到梯度，并进行梯度下降。一定注意，是通过对损失函数进行梯度下降，来得到参数值！

比如我们用到的损失函数为：$J(\theta )=\frac{1}{2m}(X\theta -Y{)}^T(X\theta -Y)$。

里面的参数为$\theta$,因此应对$\theta$进行求导，其中$J$为标量，因此求导得到的是梯度，这就涉及到了矩阵求导术，移步知乎大神https://zhuanlan.zhihu.com/p/24709748

此文章从标量求导引向矩阵求导，不仅介绍了如何求导，还介绍了很多数学思想，如数学追求整体性，相似性，定义不方便计算我们要创造公式定理，等等。

矩阵求导的本质其实是逐项求导。

或者直接看矩阵求导的公式：https://blog.csdn.net/WPR1991/article/details/82929843

$J$对$\theta$进行求导，主要用到两个公式，一个是矩阵求导链式法则，一个是矩阵求导中的对转置相乘进行求导，这类似与标量的平方求导。

得到：$▽J=\frac{1}{m}{X}^T(X\theta -Y)$或者$▽J=\frac{1}{m}X(X\theta -Y{)}^T$

2.python手写实现

不管用什么语言实现，其本质都是通过矩阵运算实现的算法。下面算法的前置知识为：矩阵内积，上述梯度，numpy（实现矩阵运算）。

2.1实例描述

首先我们通过代码实现一个线性回归模型。然后通过梯度下降法对此模型进行拟合。

2.2代码实现

import numpy as np
import matplotlib.pyplot as plt
#第一步创建要拟合的模型
# 随机生成1000个点，围绕在y=0.1x+0.3的直线周围
X=[]
Y=[]
np.random.seed(10)
m=1000
a=0.5#学习率
for i in range(1000):
    x = np.random.normal(0., 0.55)  # 产生均值为0，方差为0.55的随机的正态分布
    y = 0.1 * x + 0.3
    y=y+np.random.normal(0,0.2)
    X.append(x)
    Y.append(y)
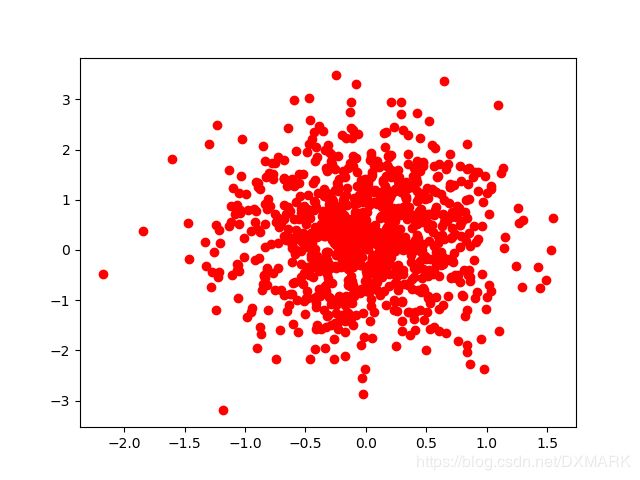
plt.scatter(X,Y,c='r')#散点图
plt.show()

运行结果：

#第二步
#通过梯度下降法进行拟合
#已知为一次函数模型，初始化参数为a=1，b=0
theta=[1,0]
theta=np.array(theta)
theta=theta.reshape(2,1)#2*1
for i in range(m):
    X.append(1)
X=np.array(X)
X=X.reshape(2,m).transpose()#m*2
Y=np.array(Y)
Y=Y.reshape(1000,1)
#print(np.shape(Y))
def loss(X,Y,m,theta):#求损失函数
    diff=(np.dot(X,theta)-Y)#1000*1
    l=np.dot(diff.transpose(),diff)/(2*m)
    return l[0][0]

def gradient(X,theta,Y):#应为2*1向量
    diff = (np.dot(X,theta) - Y)#1000*1
    g=np.dot(X.transpose(),diff)/m#2*1000  1000*1
    return g

def gradient_function(X,Y,a,theta):#a:学习率，theta：参数，Python里的递归调用是有限制的,打开终端运行Python，可以看到默认限制值为1000
    theta = theta-a*gradient(X,theta,Y)
    return theta
for a in [0.01,0.1,0.5]:#以三种学习率进行对比
    for i in range(10):  # 迭代次数
        theta = gradient_function(X, Y, a, theta)
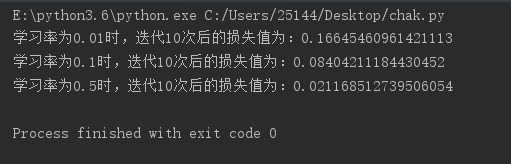
    print('学习率为{0}时，迭代10次后的损失值为：{1}'.format(a,loss(X, Y, m, theta)))

可以看到，学习率越大，学习速度越快。

3. Tensorflow实现

import numpy as np
import tensorflow as tf
import matplotlib.pyplot as plt

# 随机生成1000个点，围绕在y=0.1x+0.3的直线周围
num_points = 1000
vectors_set = []
for i in range(num_points):
    x1 = np.random.normal(0.0, 0.55)
    y1 = x1 * 0.1 + 0.3 + np.random.normal(0.0, 0.03)
    vectors_set.append([x1, y1])

# 生成一些样本
x_data = [v[0] for v in vectors_set]
y_data = [v[1] for v in vectors_set]

plt.scatter(x_data,y_data,c='r')#散点图
plt.show()

# 生成1维的W矩阵，取值是[-1,1]之间的随机数
W = tf.Variable(tf.random_uniform([1], -1.0, 1.0), name='W')#tf.random_uniform((4, 4), minval=low,maxval=high,dtype=tf.float32)))返回4*4的矩阵，产生于low和high之间，产生的值是均匀分布的。
# 生成1维的b矩阵，初始值是0
b = tf.Variable(tf.zeros([1]), name='b')
# 经过计算得出预估值y
y = W * x_data + b

# 以预估值y和实际值y_data之间的均方误差作为损失
loss = tf.reduce_mean(tf.square(y - y_data), name='loss')
# 采用梯度下降法来优化参数
optimizer = tf.train.GradientDescentOptimizer(0.5)
# 训练的过程就是最小化这个误差值
train = optimizer.minimize(loss, name='train')

sess = tf.Session()

init = tf.global_variables_initializer()
sess.run(init)

# 初始化的W和b是多少
print ("W =", sess.run(W), "b =", sess.run(b),"loss =", sess.run(loss))
# 执行20次训练
for step in range(20):
    sess.run(train)
    # 输出训练好的W和b
    print ("W =", sess.run(W), "b = " , sess.run(b),"loss =",sess.run(loss))
#writer = tf.train.SummaryWriter("./tmp", sess.graph)

W = [0.31077862] b = [0.] loss = 0.10104149
W = [0.25170934] b =  [0.29305536] loss = 0.008323741
W = [0.20319667] b =  [0.2946985] loss = 0.0043550613
W = [0.17000362] b =  [0.29604805] loss = 0.0024961547
W = [0.14728619] b =  [0.2969714] loss = 0.0016254288
W = [0.13173832] b =  [0.29760337] loss = 0.0012175746
W = [0.12109731] b =  [0.2980359] loss = 0.0010265326
W = [0.11381457] b =  [0.2983319] loss = 0.0009370472
W = [0.10883024] b =  [0.29853448] loss = 0.0008951316
W = [0.10541896] b =  [0.29867312] loss = 0.00087549805
W = [0.10308426] b =  [0.29876804] loss = 0.0008663014
W = [0.10148638] b =  [0.29883298] loss = 0.0008619939
W = [0.1003928] b =  [0.29887742] loss = 0.00085997605
W = [0.09964434] b =  [0.29890785] loss = 0.00085903093
W = [0.0991321] b =  [0.29892868] loss = 0.0008585882
W = [0.09878152] b =  [0.29894292] loss = 0.00085838075
W = [0.09854158] b =  [0.29895267] loss = 0.00085828366
W = [0.09837736] b =  [0.29895934] loss = 0.00085823814
W = [0.09826497] b =  [0.2989639] loss = 0.0008582169
W = [0.09818805] b =  [0.29896703] loss = 0.00085820677
W = [0.0981354] b =  [0.29896918] loss = 0.00085820217

plt.scatter(x_data,y_data,c='r')
plt.plot(x_data,sess.run(W)*x_data+sess.run(b))
plt.show()