NE(Network Embedding)论文小览

#NE(Network Embedding)论文小览

自从word2vec横空出世，似乎一切东西都在被embedding，今天我们要关注的这个领域是Network Embedding，也就是基于一个Graph，将节点或者边投影到低维向量空间中，再用于后续的机器学习或者数据挖掘任务，对于复杂网络来说这是比较新的尝试，而且取得了一些效果。
本文大概梳理了最近几年流行的一些方法和论文，paper主要是来自thunlp/NRLPapers 这个List，并掺杂了一些其他论文。大概看了一遍，简单总结一下，希望对大家有所帮助，如有不严谨的地方，还望指正。
抛开一些传统的流形学习方法不谈，下面大概以这个outline组织（区分并不严格）：

##DeepWalk(Online Learning of Social Representations.)
DeepWalk是KDD 2014的一篇文章，彼时word2vec在文本上的成功应用掀起来一波向量化的浪潮，word2vec是根据词的共现关系，将词映射到低维向量，并保留了语料中丰富的信息。DeepWalk算法思路其实很简单，对图从一个节点开始使用random walk来生成类似文本的序列数据，然后将节点id作为一个个「词」使用skip gram训练得到「词向量」。
思路虽然简单，背后是有一定道理的，后面一些工作有证明这样做其实等价于特殊矩阵分解(Matrix Factorization)。而DeepWalk本身也启发了后续的一系列工作。

node2vec(Scalable Feature Learning for Networks)

node2vec在DW的基础上，定义了一个bias random walk的策略生成序列，仍然用skip gram去训练。
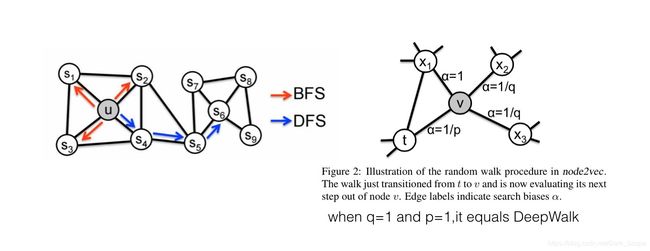
论文分析了BFS和DFS两种游走方式，保留的网络结构信息是不一样的。
DeepWalk中根据边的权重进行随机游走，而node2vec加了一个权重调整参数α：t是上一个节点，v是最新节点，x是候选下一个节点。d(t,x)是t到候选节点的最小跳数。
通过不同的p和q参数设置，来达到保留不同信息的目的。当p和q都是1.0的时候，它等价于DeepWalk。

MMDW(Max-Margin DeepWalk Discriminative Learning of Network Representation)

DW本身是无监督的，如果能够引入label数据，生成的向量对于分类任务会有更好的作用。
之前提到过有证明DW实际上是对于一个特殊矩阵M的分解，
这篇文章将DeepWalk和Max-Margin（SVM）结合起来，从损失函数看是这两部分组成：
1.训练的时候是分开优化，固定$X$,$Y$优化$W$和$\xi$，其实就是multi class 的 SVM。
2.固定$W$和$\xi$优化$X$,$Y$的时候稍微特殊一点，算了一个biased Gradient，因为损失函数里有x和w的组合。
这样在训练中同时优化discrimination和representation两部分,达到一个好的效果。

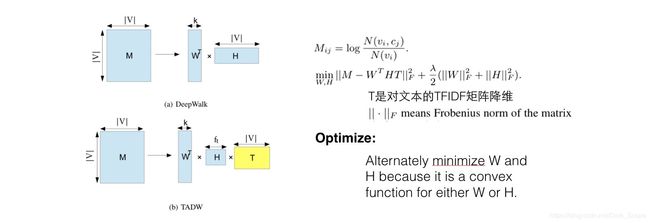
TADW(Network Representation Learning with Rich Text Information.)

文章里有DeepWark等同于M的矩阵分解的简单证明，而在实际中，一些节点上旺旺会有文本信息，所以在矩阵分解这个框架中，将文本直接以一个子矩阵的方式加入，会使学到的向量包含更丰富的信息。
文本矩阵是对TFIDF矩阵的SVD降维结果。

GraRep(Learning Graph Representations with Global Structural Information.)

沿用矩阵分解的思路，分析了不同k-step（random walk中的步数）所刻画的信息是不一样的：

所以可以对每一个step的矩阵作分解，最后将每个步骤得到的向量表示拼接起来最为最后的结果。论文中有完整的推导过程，这里就不赘述了。

LINE(Large scale information network embedding)

LINE分析了1st order proximity和2nd order proximity，其中一度相似性就是两个点直接相连，且边权重越大说明两个点越相似，如下图中的6和7；而二度相似性则是两个点之间共享了很多邻居，则它们的相似性就很高，如下图的5和6。
文章中非常简单的方式构造了一个目标函数，能同时保留二者的信息。以一度相似性为例，节点i和j相连的经验概率就是和归一化后的权重，即${\hat{p}}_1(i,j)=w_{ij}/W$，而通过向量计算这个概率值是$p_1(i,j)=\frac{1}{1+exp(-u_i^T{u}_j)}$，目标函数就是让这两个分布距离最小，选择KL散度作为距离衡量函数就得到了最后的损失函数$O_1$。
其中还有个优化的trick，edge-sampling algorithm：因为边的weight差异很大，直接用SGD效果不好，所以有个edge的采样，按照边的weight采样，然后每条边当做binary的算。

NEU(Fast Network Embedding Enhancement via High Order Proximity Approximation)

这一篇是最近发表在IJCAI上的文章，说实话是一个很取巧的方式，文章分析了一些可以视为矩阵分解的embedding方法：

得到一个结论，如果矩阵分解$f(A)=RC$能更精确地包括高阶信息，效果是会更好的，但带来的结果是算法的计算复杂度更高。
所以文章采用一种很巧妙的方式，在（低阶low-order）矩阵分解的结果上更新，以获得更高阶（higher order）的分解结果，使最后的向量效果更好，这个方法是可以适用在多个算法中的。
论文中证明了一个bound来支持这样的更新方式。

Extra Info

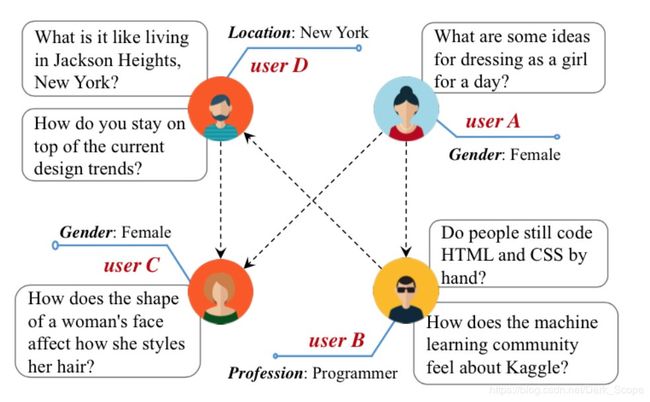
前面我们看的绝大多数只考虑了网络结构，但真实世界中的节点和边往往都会含有丰富的信息。如上图，在Quora场景中，每个用户自身会有一些label和文本，在一些场景里甚至边也会带上一些label，这些信息对于网络的构建其实是至关重要的，前面我们也看到了TADW将节点的文本信息纳入训练，下面罗列一些这个方向相关的论文。

CANE(Context-Aware Network Embedding for Relation Modeling)

首先考虑了节点上的Context，主要是文本，学习对每个节点产出Vt（文本向量）和Vs（结构向量）
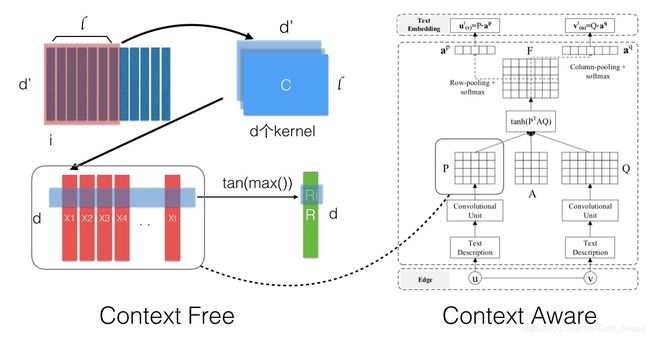
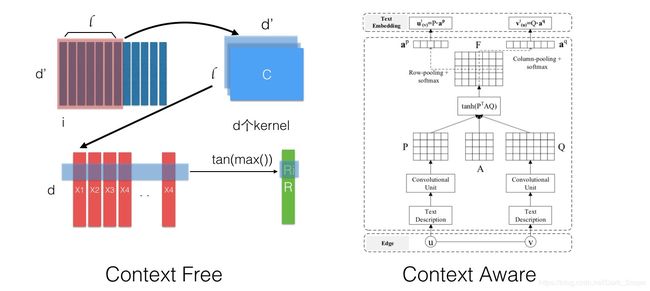
Context-Free的话Vt是固定的，采用一个CNN的流程产出，如下图左边部分：对于一个文本，每个词的向量组成一个矩阵，然后以$l$为窗口在d个kernel上进行CNN的卷积操作，得到的结果按行取max来获得最后的文本向量。
Context-Aware的话引入了Attention机制，会考虑边e=(u,v)的tu和tv，通过下右图的流程产出Attention权重，再进行类似Pooling的操作（最后一步），这样节点在和不同的点连接的时候其作用是不一样的。
A是引入的待训练参数，物理意义可能为目标维的空间变换。

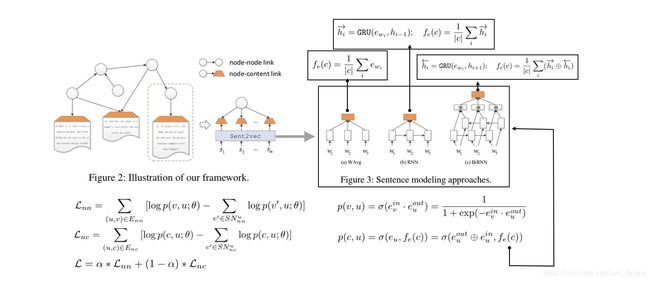
CENE(A General Framework for Content-enhanced Network Representation Learning)

这篇文章将文本转化为特殊的节点，这样就有两种连边，(节点-文档)以及(节点-节点)，对两种边一起建模，损失函数包括$L_{nn}$和$L_{nc}$，其中文本拆分为更细的句子，而句子有三种方式去embedding，下面有列举。
和很多方法一样，Loss的减数部分是负采样出来的。

Trans-Net(Translation-Based Network Representation Learning for Social Relation Extraction)

这篇paper也是最新2017在IJCAI上发表的，引入了机器翻译的思想，将Translation机制应用到中间，通过一个Autoencode对边上的labels(构成一个向量)进行编码，然后将节点和edge映射到同一个空间作加减。认为在这个空间里u+l=v’（每个节点有两个向量表示，分别指示在边的「起点」和「终点」时，用’进行区分）
这样预测的时候，简单用v’-u 就可以得到l，再用AE的解码器部分还原为element-binary的label set，就得到预测结果。

##Deep Learning
最近几年深度学习如火如荼，严格来说，类似word2vec其实属于浅层模型，但你也可以用一些复杂的深度模型去获得embedding结果，这个思路是将网络序列化，借用NLP的方法去训练。

我们知道在图像上做CNN就是对临接的像素进行卷积操作，那么如果直接对图作CNN呢？这就是GCN的思路，但这里并不详细介绍GCN，看上图应该能明白它是怎么去做的。
还有一些工作将深度学习应用到了Network Embedding上面，之前罗列的比如CANE和Trans-Net都有这样的结构，特别是Trans-Net使用的Autoencoder就是一个神经网络。
深度学习有很多工作都是基于一整个Graph去做的，比如判断一个Graph的某些属性，本文主要是列举对节点进行embedding的方法。

###SSC-GCN(Semi-Supervised Classification with Graph Convolutional Networks)

https://github.com/tkipf/gcn
http://tkipf.github.io/graph-convolutional-networks/

和DW完全不同的思路，引入了一个spectral convolutions操作，不过目前看起来卷积是在整个图上做的，还没有支持mini-batch，最后目标是单个节点的分类和表示学习。
在之前的一些工作中，NN for graph都是对图级别做的，做分类等等，针对整个sub-graph，但这里本质上还是对单个节点。

这里的操作是这个意思：比如说下图X中每一行是一个图节点的input feature表示，那么通过A和W可以一次次改变这个矩阵的列数，其实就是在做「全连接」操作，只是A可能是稀疏的（转移矩阵），所以可以看成是某种卷积操作，每一步将与之相连的节点的权重信息汇合到输出的这一行中。

最后定义了一个semi-supervised的东西，可以将部分节点的label也作为loss的一部分，所以整体的损失函数是：

其中L0是有监督的部分，后面的$L_{reg}$实际上包含了边的信息，其中$A$是描述了所有边信息的adjacency matrix(or some function thereof).
比较有意思的是，这个网络甚至随机初始化，不训练，得到的结果分布都比较清晰（不同community的点最后会映射得比较接近），论文解释这个计算本身的逻辑有点像Weisfeiler-Lehman算法。

###SDNE(Structural Deep Network Embedding)

中间有一部分逻辑和TransNet有点类似，它是对节点的描述特征向量（比如点的「邻接向量」）使用autoencoder编码，同时也对非0项加重惩罚了（没有连接并不代表一定没有，可能只是还没发生，所以这里对此进行了协调）：取autoencoder中间层作为向量表示，以此来让获得2nd proximity（相似邻居的点相似度较高，因为两个节点的「邻接向量」相似，说明它们共享了很多邻居，最后映射成的向量y也会更接近）。
对于1st proximity，通过评估有连边的点的vector距离来纳入考虑。
这两部分都纳入最后的损失函数，这里的$L_{reg}$是正则。
不然过这个计算要传入「邻接向量」进去的话，对于节点特别多的情况是个负担。

##Heterogeneous
真实世界中的网络毫无疑问是异构的(Heterogenous)，比如交易中，涉及到的节点有人、商品、店铺等等；更一般的比如知识图谱中有不同类型的节点和边，而前面描述的绝大部分工作都是在同构网络(Homogenous)的基础上进行的，所以了解异构网络的embedding对真正在实际中的应用会有帮助。

###PTE(Predictive Text Embedding through Large-scale Heterogeneous Text Networks.)

这篇文章的主要意图是将predictive的信息在最后的embedding提现出来，但不要像CNN/RNN模型那样直接嵌套一个复杂的预测模型。所以他分别定义了三种network，word-word,word-document,word-label。都搞成类似二部图的样子，然后将各自的损失函数汇总到一起（形式都是类似的，定义经验概率和目标概率求KL距离），就是这么简单粗暴。

###HINES(Heterogeneous Information Network Embedding for Meta Path based Proximity)

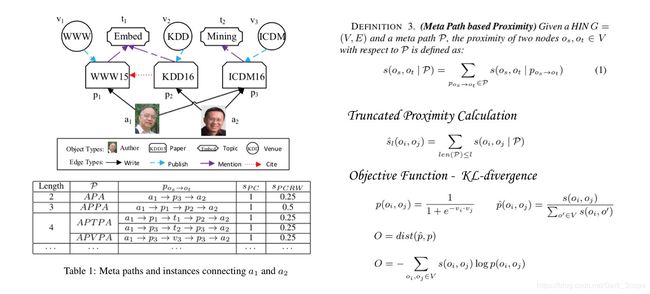
这篇文章对多元异构网络（知识图谱）进行了embedding，图中有不同类型的点，不同类型的连边。引入了meta path的概念，就是不同点之间的连边是按照一定的元信息连起来的，比如A1(Author)-P1(Paper)-A2(Author)这样一个meta path表示的信息可能就是A1和A2之间合作了一篇paper，这个概念可以很好地推广到很多场景。
一般在计算proximity的时候都是按照1st order这样的思路来的，但引入了meta path概念的时候，如果A和B在一条meta path的两端，那么它们的proximity应该更大，当然这也取决于这条元路径本身的信息量。
文章中选择了所有长度小于l的元路径，因为一般来说路径越长其信息量越少。
最后的损失函数同样是刻画分布的距离。

##总结
Network Embedding是最近几年还是有蛮多工作的，这里只列举了一些。虽然NE从NLP里借鉴了很多的思想，但二者还是有一些不同的，a.如果以节点id作为「词」，那么对于一些真实的网络来说，可能会非常稀疏，而且节点的数量会非常大，上亿是很正常的，这对上面一些方法的应用有一些限制，你可以想象存这样大的一张此表需要多大的内存。b.异构网络如何能够更好地被训练，是一个很有挑战的事情；同时节点和边上往往有着各种丰富的信息，如何能够将这些信息都学到结果向量中，也是很有意思的。

本文并没有非常详细地去讲每篇论文，只是记录了主要思路，有兴趣可以去读原始论文。

##Reference
【0】上面每一个子标题括号中的内容就是对应的论文题目。
【1】THUNLP_NRLpapers
【2】《Representation Learning with Networks》by Jure Leskovec.slide_01