字符串模式匹配之KMP
1 场景
假设现在我们面临这样一个问题:有一个主串(文本串)S,和一个模式串P,现在要查找P在S中的位置,怎么查找呢?
2 暴力法
2.1 思想
如果使用暴力匹配的思路,并假设现在主串S匹配到 i 位置,模式串P匹配到 j 位置,则有:
- 如果匹配(即S[i] == P[j]),则i++,j++,继续匹配下一个字符;
- 如果失配(即S[i]! = P[j]),令i = i - j + 1,j = 0。相当于每次匹配失败时,i 回溯 ,j 被置为0。
2.2 代码
public static int violentMatch(String s, String p) {
int sLen = s.length();
int pLen = p.length();
int i = 0;//主串遍历指针
int j = 0;//模式串遍历指针
while (i < sLen && j < pLen) {
if (s.charAt(i) == p.charAt(j)) {//如果匹配,则i++,j++;
i++;
j++;
} else {//如果失配,令i = i - (j - 1),j = 0;
i = i - j + 1;
j = 0;
}
}
//匹配成功,返回模式串p在文本串s中的位置,否则返回-1
if (j == pLen) return i - j;
else return -1;
}
2.3 举例
举个例子,如果给定文本串S=“BBC ABCDAB ABCDABCDABDE”,和模式串P=“ABCDABD”,现在要拿模式串P去跟文本串S匹配,整个过程如下所示:






3 KMP
3.1KMP匹配过程
3.1.1 匹配思想
下面先直接给出KMP的算法流程:假设现在文本串S匹配到 i 位置,模式串P匹配到 j 位置;
- 如果j == -1,或匹配成功(即S[i] == P[j]),令i++,j++,继续匹配下一个字符;
- 如果j != -1,且匹配失败(即S[i] != P[j]),则令 i 不变,j = next[j];
下面是对上面思想的一些解释或者补充:
- 失配时,i不变,不回溯,下一个 j =next [ j ];
- 失配时,相当于模式串右移 j - next [ j ] 位;
- j - next [ j ]可以解释为:已匹配字符数 - 失配字符的前一字符的最大长度值(后面会解释这个最大长度值);
- j - next [ j ]还可以解释为:失配字符的位置 - 失配字符对应的next 值;
3.1.2 匹配代码
public static int kmpMatch(String s, String p) {
int i = 0;
int j = 0;
int sLen = s.length();
int pLen = p.length();
int [] next=new int[pLen];
getNext(p,next);//先求模式串p的next数组
while (i < sLen && j < pLen) {//KMP匹配过程
if (j == -1 || s.charAt(i) == p.charAt(j)) {//如果j == -1,或匹配成功,令i++,j++ ;
i++;
j++;
} else {//如果j != -1,且失配,则令 i 不变,j = next[j]不回溯
j = next[j];
}
}
if (j == pLen)
return i - j;
else
return -1;
}
3.1.3 失配时举例
- 继续2.3的例子来说,当S[10]跟P[6]匹配失败时,KMP不再是像暴力匹配那样简单的把模式串右移一位,而是执行这条指令:“如果j != -1,且匹配失败(即S[i] != P[j]),则令 i 不变,j = next[j]”,即j 从6变到next[6]=2,所以相当于模式串向右移动的位数为j - next[j](j - next[j] = 6-2 = 4);

- 向右移动4位后,S[10]跟P[2]继续匹配;为什么要右移4位呢?因右移4位后,模式串中又有个“AB”可以继续跟S[8]S[9]对应着,从而不用让i 回溯;减少没必要的比较;

这只是一个匹配失败时的举例,基于KMP的完整匹配过程会在后面给出。
3.2 最长公共前缀后缀的长度
3.2.1 定义
对于某一个字符串,它的前缀、后缀分别定义为:
- 前缀:不包含尾字符,必须包含首字符的连续子串;
- 后缀:不包含首字符,必须包含为字符的连续子串;
例如:给定字符串P “abcba”,P的前缀集合为{ a , ab , abc , abcb },前缀集合为{ bcba , cba , ba , a } ;P的公共前缀后缀只有一个{ a },所以P的最长公共前缀后缀的长度为1;
3.2.1 求最长公共前缀后缀的长度
对于2.3中给的例子,模式串P=“ABCDABD”,其各个前子串的前缀后缀分别如下表格所示:
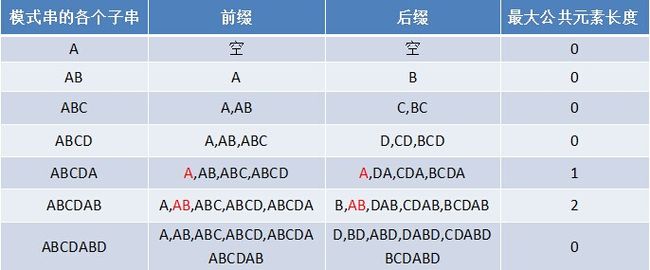
也就是说,模式串各个前子串对应的最长公共前缀后缀长度表为(下简称《最大长度表》):

3.3 next数组
3.3.1 next数组的人工求法
next 数组的求法:最大长度表右移一位,next [0]赋值为-1;
对于2.3中给的例子,模式串P=“ABCDABD”,其最大长度表和next 数组表为:

3.3.2 next数组递推(动态规划)算法:
已知next [0, …, j],如何求next [j + 1]呢?
首先j为0时, next [ j ] = -1;假设k= next [ j ];然后执行下面递归过程:
- 当p[k] == p[j]或者 k为-1时,则next[ j + 1 ] = next [ j ] + 1 = k + 1;
- 当p[k] != p[j]且k不为-1时,k=next [k];
下面是一些补充或解释:
- 解释:
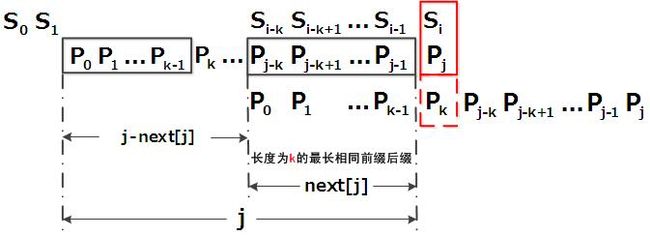
(1)已知k=next [ j ],所以在pj前存在p0 p1, …, pk-1 = pj-k, pj-k+1, …, pj-1;
(2)现在要求next [ j+1 ],先判断pk?=pj;如果相等,那么pj+1前存在p0 p1, …, pk-1,pk = pj-k, pj-k+1, …, pj-1,pj长度为k+1的最大公共前缀后缀,所以next[ j + 1 ] = k + 1;
(3)如果pk!=pj,就去找一个长度更小的公共前缀后缀;递归比较pnext [k]?=pj,如果相等,则next[ j + 1 ] = k + 1 = next [ k ] + 1;否则继续让k=next [k],然后比较pk!和pj;
-
至于为什么递归地令(下一个)k=next [k]就能够找到的长度更小的公共前缀后缀,我的理解是模式串的自我匹配;详情可以参考原文博客;
-
求next数组其实就是一个动态规划问题,dp方程为next[ j + 1 ] = next [ j ] + 1 ;
3.3.4 代码
public static void getNext(String p,int [] next){
int pLen = p.length();
int j = 0;
next[j] = -1;
int k = next[j];
while (j < pLen - 1) {
//p[k]表示前缀,p[j]表示后缀
if (k == -1 || p.charAt(j) == p.charAt(k)) {
next[++j] = ++k;
} else {
k = next[k];
}
}
}
用代码重新计算下“ABCDABD”的next 数组:
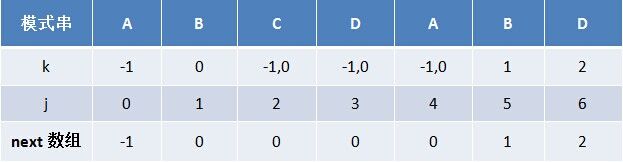
3.4 使用 next数组的KMP匹配完整过程举例
还是之前2.2的例子,文本串S=“BBC ABCDAB ABCDABCDABDE”,模式串P=“ABCDABD”:
- 先求next数组,上一节已经求出;


- 最开始匹配时,P[0]跟S[0]匹配失败,所以执行“如果j != -1,且当前字符匹配失败(即S[i] != P[j]),则令 i 不变,j = next[j]”,所以j = -1,故转而执行“如果j = -1,或者当前字符匹配成功(即S[i] == P[j]),都令i++,j++”,得到i = 1,j = 0,即P[0]继续跟S[1]匹配;P[0]跟S[1]又失配,j再次等于-1,i、j继续自增,从而P[0]跟S[2]匹配
;P[0]跟S[2]失配后,P[0]又跟S[3]匹配;P[0]跟S[3]再失配,直到P[0]跟S[4]匹配成功,开始执行此条指令的后半段:“如果j = -1,或者当前字符匹配成功(即S[i] == P[j]),都令i++,j++”;

- P[1]跟S[5]匹配成功,P[2]跟S[6]也匹配成功, …,直到当匹配到P[6]处的字符D时失配(即S[10] != P[6]),由于P[6]处的D对应的next 值为2,所以下一步用P[2]处的字符C继续跟S[10]匹配,相当于向右移动:j - next[j] = 6 - 2 =4 位;

- 向右移动4位后,P[2]处的C再次失配,由于C对应的next值为0,所以下一步用P[0]处的字符继续跟S[10]匹配,相当于向右移动:j - next[j] = 2 - 0 = 2 位;

- 移动两位之后,A 跟空格不匹配,模式串后移1 位;
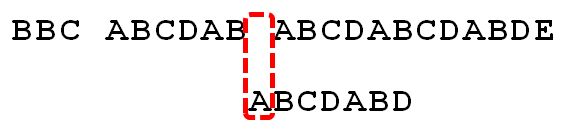
- P[6]处的D再次失配,因为P[6]对应的next值为2,故下一步用P[2]继续跟文本串匹配,相当于模式串向右移动 j - next[j] = 6 - 2 = 4 位;

- 匹配成功,过程结束;

3.5 next数组优化
3.5.1 存在问题
用之前的next 数组方法求模式串“abab”的next 数组,可得其next 数组为-1 0 0 1(0 0 1 2整体右移一位,初值赋为-1),当它跟下图中的文本串去匹配的时候,发现b跟c失配,于是模式串右移j - next[j] = 3 - 1 =2位。
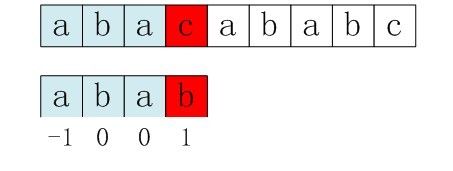
右移2位后,b又跟c失配。事实上,因为在上一步的匹配中,已经得知p[3] = b,与s[3] = c失配,而右移两位之后,让p[ next[3] ] = p[1] = b 再跟s[3]匹配时,必然失配。问题出在哪呢?
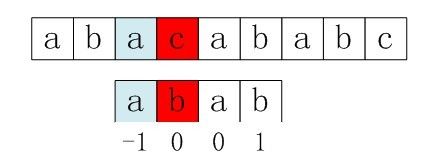
问题出在:当出现p[j] = p[ next[j] ]时,这次比较是非必要的。为什么呢?理由是:当p[j] != s[i] 时,下次匹配必然是p[ next [j]] 跟s[i]匹配,如果p[j] = p[ next[j] ],必然导致后一步匹配失败(因为p[j]已经跟s[i]失配,然后你还用跟p[j]等同的值p[next[j]]去跟s[i]匹配,很显然,必然失配),所以不能允许p[j] = p[ next[j ]]。如果出现了p[j] = p[ next[j] ]咋办呢?如果出现了,则需要再次递归,即令next[j] = next[ next[j] ]。
3.5.2 优化策略
优化策略:当出现p[j] = p[ next[j ]]时,再次递归,令next[j] = next[ next[j] ];
ps:当然优化后,仍然可能会出p[j] = p[ next[j ]]=p[ next[ next[j ] ]],我们可以再递归一次;当然满足这种这种场景的出现是小概率事件,也就没必要再递归一次了;
只要求出了原始next 数组,便可以根据原始next 数组快速求出优化后的next 数组。还是以abab为例,如下表格所示:
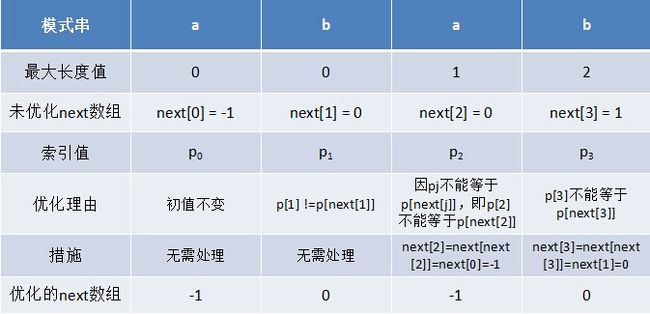
3.5.3 代码
public static void getNext(String p,int [] next){
int pLen = p.length();
int j = 0;
next[j] = -1;
int k = next[j];
while (j < pLen - 1) {
//p[k]表示前缀,p[j]表示后缀
if (k == -1 || p.charAt(j) == p.charAt(k)) {
//当p[k] == p[j]或者 k为-1时,则next[ j + 1 ] = next [ j ] + 1 = k + 1
++j;
++k;
if (p.charAt(j) == p.charAt(k)) {
//优化处理:当出现p[j] = p[next[j]]时,再次递归,k = next[k];
next[j] = next[k];
}else {
next[j]= k;
}
} else {//当p[k] != p[j]且k不为-1时,k=next [k];
k = next[k];
}
}
}
4 时间复杂度
假设主串长度为n,模式串长度为m;
暴力法时间复杂度为O(m*n);
KMP算法求next数组时间复杂度为O(m),匹配过程时间复杂度为O(m),总的时间复杂度为O(m+n);
转自:从头到尾彻底理解KMP