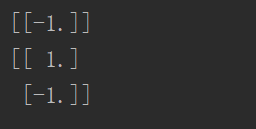【机器学习】AdaBoost算法Python实现

回顾

集成学习，这里我们先介绍了集成学习的相关知识，集成学习就是通过构建并结合多个学习器来完成学习任务。 然后根据个体学习器的生成方式，介绍了集成学习方法两大类：

• 个体学习器间存在强依赖关系，必须串行生成的序列化方法，代表是：Boosting
• 个体学习器间不存在强依赖关系，可同时生成的并列化方法，代表是：Bagging和随机森林（Random Forest）

AdaBoost算法，这里我们具体介绍了 AdaBoost算法 A d a B o o s t 算 法 的流程。

再看本博客前，可先看前两篇有助于理解本篇代码。

AdaBoost A d a B o o s t 运行过程

训练数据中的每一个样本，并赋予其一个权重，这些权重构成一个向量 D D 。一开始，这些权重都初始化成相等值。

首先在训练数据上训练出一个弱分类器并计算该分类器的错误率，然后在同一个数据集上再次训练弱分类器。在分类器的第二次训练当中，将会重新调整每个样本的权重，其中每一个分对的样本的权重会下降，而第一次分错的样本的权重会提高。

为了从所有弱分类器中取得最终的分类结果， AdaBoost A d a B o o s t 为每一个分类器都分配了一个权重值 α α ，这些 α α 值是基于每个分类器的错误率进行计算的。

其中，错误率 ε ε 的定义为：

ε=未正确分类的样本数目所有样本数目 ε = 未 正 确 分 类 的 样 本 数 目 所 有 样 本 数 目

而 α α 的计算公式为：

α=12ln(1−εε) α = 1 2 l n ( 1 − ε ε )

计算出 α α 值后，可以对权重向量 D D 进行更新，以使得那些分类正确的样本的权重降低而错分样本的权值升高。 D D 的计算方法如下：

D(t+1)t=⎧⎩⎨⎪⎪⎪⎪⎪⎪⎪⎪D(t)te−αSum(D)样本被正确分类D(t)teαSum(D)样本被错误分类 D t ( t + 1 ) = { D t ( t ) e − α S u m ( D ) 样 本 被 正 确 分 类 D t ( t ) e α S u m ( D ) 样 本 被 错 误 分 类

在计算出权重向量 D D 后， AdaBoost A d a B o o s t 开始下一次迭代。 AdaBoost A d a B o o s t 不停地迭代直到训练错误率为0或者达到指定的迭代次数。

这里涉及到的公式在 AdaBoost A d a B o o s t 算法讲解中都有推导，可参考前面的博客。

下面我们就来一步步通过 Python3 P y t h o n 3 来实现 AdaBoost A d a B o o s t 算法。

基于单层决策树构建弱分类器

单层决策树是一种简单的决策树，这里我们介绍过决策树，而单层决策树仅基于单个特征来做决策。

首先我们先准备一些数据，如下：

from numpy import *

def loadSimpleData():
    datMat = matrix(
        [[1., 2.1],
         [2., 1.1],
         [1.3, 1.],
         [1., 1.],
         [2., 1.]]
    )
    classLabels = [1.0, 1.0, -1.0, -1.0, 1.0]
    return datMat, classLabels

数据可视化：

from numpy import *
import matplotlib.pyplot as plt

datMat = matrix([[1., 2.1],
                 [1.5, 1.6],
                 [1.3, 1.],
                 [1., 1.],
                 [2., 1.]])
classLabels = [1.0, 1.0, -1.0, -1.0, 1.0]

xcord0 = []
ycord0 = []
xcord1 = []
ycord1 = []
markers = []
colors = []

for i in range(len(classLabels)):
    if classLabels[i] == 1.0:
        xcord1.append(datMat[i, 0]), ycord1.append(datMat[i, 1])
    else:
        xcord0.append(datMat[i, 0]), ycord0.append(datMat[i, 1])
fig = plt.figure()
ax = fig.add_subplot(111)
ax.scatter(xcord0, ycord0, marker='s', s=90)
ax.scatter(xcord1, ycord1, marker='o', s=50, c='red')
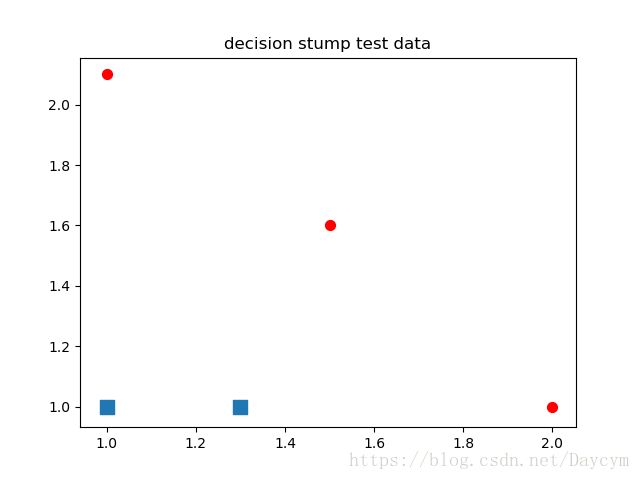
plt.title('decision stump test data')
plt.show()

运行结果1：

单层决策树生成函数

伪代码：

将最小错误率minError设为 +∞ + ∞
对数据集中的每一个特征（第一层循环）：
         对每一个步长（第二层循环）：
                 对每个不等号（第三层循环）：
                        建立一棵单层决策树并利用加权数据集对它进行测试
                        如果错误率低于minError，则将当前单层决策树设为最佳单层决策树
返回最佳单层决策树

代码：

# 单层决策树生成函数
# 通过阀值比较对数据进行分类，在阀值一边的数据分到类别-1，而在另一边的数据分到类别+1
def stumpClassify(dataMatrix, dimen, threshVal, threshIneq):  # 数据集，数据集列数，阈值，比较方式：lt，gt
    retArray = ones((shape(dataMatrix)[0], 1))  # 将数组的全部元素设置为1

    # lt：小于，gt；大于；根据阈值进行分类，并将分类结果存储到retArray
    if threshIneq == 'lt':
        retArray[dataMatrix[:, dimen] <= threshVal] = -1.0
    else:
        retArray[dataMatrix[:, dimen] > threshVal] = -1.0
    return retArray  # 返回分类结果


# 遍历stumpClassify()函数所有的可能输入值，并找到数据集上的最佳的单层决策树
def buildStump(dataArr, classLabels, D):  # 数据集，数据标签，权重向量
    dataMatrix = mat(dataArr)  # 使输入数据符合矩阵格式
    labelMat = mat(classLabels).T  # 标签，转置为列向量
    m, n = shape(dataMatrix)  # 矩阵形状，m为样本个数，n为每个样本的特征个数
    numSteps = 10.0  # 初始化步数，用于在特征的所有可能值上进行遍历
    bestStump = {}  # 创建一个空字典，用于存储给定权重向量D时所得到的最佳决策树的相关信息
    bestClasEst = mat(zeros((m, 1)))  # 初始化类别估计值
    minError = inf  # 一开始初始化为正无穷大，之后用于寻找可能的最小错误率

    for i in range(n):  # 遍历数据集的所有特征
        rangeMin = dataMatrix[:, i].min()
        rangeMax = dataMatrix[:, i].max()
        stepSize = (rangeMax - rangeMin) / numSteps  # 通过计算最大值和最小值差值除以步数来确定步长
        for j in range(-1, int(numSteps) + 1):  # 遍历每个步长
            for inequal in ['lt', 'gt']:  # 遍历每个大于和小于不等式
                threshVal = (rangeMin + float(j) * stepSize)  # 设定阀值
                predictedVals = stumpClassify(dataMatrix, i, threshVal, inequal)  # 调用stumpClassify函数，通过阀值比较对数据进行分类
                errArr = mat(ones((m, 1)))  # 错误列向量，将预测结果与真实类别比较，不相同则对应位置设为1
                errArr[predictedVals == labelMat] = 0  # 相同位置设为0
                weightedError = D.T * errArr  # 将错误向量和权值向量相乘并求和（横向量*列向量=对应元素相乘求和）
                # 打印结果
                print("split: dim %d, thresh %.2f, thresh ineqal: %s, the weighted error is %.3f"
                      % (i, threshVal, inequal, weightedError))
                # 如果错误率低于minError，则将当前单层决策树设为最佳单层决策树，更新各项值
                if weightedError < minError:
                    minError = weightedError
                    bestClasEst = predictedVals.copy()
                    bestStump['dim'] = i
                    bestStump['thresh'] = threshVal
                    bestStump['ineq'] = inequal
    return bestStump, minError, bestClasEst  # 返回最佳单层决策树，最小错误率，类别估计值


# 测试
D = mat(ones((5, 1)) / 5)   # 初始化权重向量
print("最佳单层决策树相关信息：", buildStump(datMat, classLabels, D))

运行结果2：

[[1.  2.1]
 [2.  1.1]
 [1.3 1. ]
 [1.  1. ]
 [2.  1. ]]
[1.0, 1.0, -1.0, -1.0, 1.0]
split: dim 0, thresh 0.90, thresh ineqal: lt, the weighted error is 0.400
split: dim 0, thresh 0.90, thresh ineqal: gt, the weighted error is 0.600
split: dim 0, thresh 1.00, thresh ineqal: lt, the weighted error is 0.400
split: dim 0, thresh 1.00, thresh ineqal: gt, the weighted error is 0.600
.
.
.
split: dim 1, thresh 2.10, thresh ineqal: lt, the weighted error is 0.600
split: dim 1, thresh 2.10, thresh ineqal: gt, the weighted error is 0.400
最佳单层决策树相关信息： ({'dim': 0, 'thresh': 1.3, 'ineq': 'lt'}, matrix([[0.2]]), array([[-1.],
       [ 1.],
       [-1.],
       [-1.],
       [ 1.]]))

完整 AdaBoost A d a B o o s t 算法实现

伪代码：

对每次迭代：
       利用buildStump()函数找到最佳的单层决策树
       将最佳单层决策树加入到单层决策树数组
       计算 α α 值
       计算新的权重向量 D D
       更新累计类别估计值
       如果错误率低于0.0，则退出循环

代码：

# 注：代码前面需要加入上面的单层决策树的代码
# 完整AdaBoost算法实现
def adaBoostTrainDS(dataArr, classLabels, numIt=40):  # 数据集，类别标签，迭代次数
    weakClassArr = []  # 建立一个空列表，用于存储单层决策树的信息
    m = shape(dataArr)[0]  # 数据集行数
    D = mat(ones((m, 1)) / m)  # 初始化向量D每个值均为1/m，D包含每个数据点的权重，在后续的迭代中会增加错误预测的权重，相应的减少正确预测的权重
    aggClassEst = mat(zeros((m, 1)))  # 初始化列向量，记录每个数据点的类别估计累计值
    for i in range(numIt):  # 遍历迭代次数，直到达到遍历次数或者错误率为0停止迭代
        bestStump, error, classEst = buildStump(dataArr, classLabels, D)  # 调用buildStump构建一个单层决策树
        # print("D:", D.T)
        alpha = float(0.5 * log((1.0 - error) / max(error, 1e-16)))  # 根据公式计算alpha的值，max(error, 1e-16)用来确保在没有错误时不会发生除零溢出
        bestStump['alpha'] = alpha  # alpha加入到字典中
        weakClassArr.append(bestStump)  # 再添加到列表
        # print("classEst:", classEst.T)

        # 计算下一次迭代中的新权重向量D
        expon = multiply(-1 * alpha * mat(classLabels).T, classEst)
        D = multiply(D, exp(expon))
        D = D / D.sum()

        aggClassEst += alpha * classEst  # 累加类别估计值，该值为浮点型
        # print("aggClassEst:", aggClassEst.T)
        aggErrors = multiply(sign(aggClassEst) != mat(classLabels).T, ones((m, 1)))  # 通过sign()函数得到二值分类结果，与真实类别标签比较，计算错误分类的个数
        errorRate = aggErrors.sum() / m  # 计算错误率
        print("total error: ", errorRate)  # 打印每次迭代的错误率

        if errorRate == 0.0:  # 如果某次迭代之后的错误率为0，就退出迭代过程，则不需要达到预先设定的迭代次数
            break
    return weakClassArr

# 测试
datMat, classLabels = loadSimpleData()
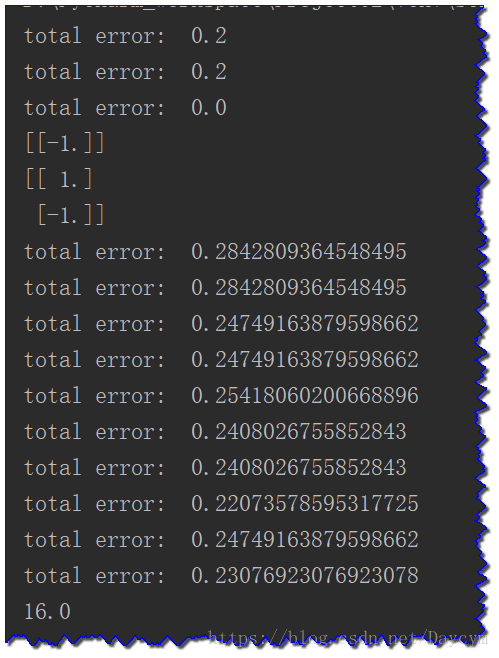
classifierArray = adaBoostTrainDS(datMat, classLabels, 9)

print(classifierArray)

运行结果3：

测试算法

代码：

# 测试算法：基于AdaBoost的分类
def adaClassify(datToClass, classifierArr):  # 待分类样本，多个弱分类器组成的数组
    dataMatrix = mat(datToClass)  # 将待分类样本转为矩阵
    m = shape(dataMatrix)[0]  # 得到测试样本的个数
    aggClassEst = mat(zeros((m, 1)))  # 构建一个O列向量，作用同上
    for i in range(len(classifierArr)):  # 遍历所有弱分类器
        # 基于stumpClassify()对每个弱分类器得到一个类别的估计值
        classEst = stumpClassify(dataMatrix, classifierArr[i]['dim'], classifierArr[i]['thresh'], \
                                 classifierArr[i]['ineq'])
        aggClassEst += classifierArr[i]['alpha'] * classEst  # 输出的类别值乘以该单层决策树的alpha权重再累加到aggClassEst上
        # print(aggClassEst)  # 打印结果
    return sign(aggClassEst)  # 返回分类结果，aggClassEst大于0则返回+1，小于0则返回-1


adaArr, labelArr = loadSimpleData()
classifierArr = adaBoostTrainDS(adaArr, labelArr, 30)
print(adaClassify([0, 0], classifierArr))

print(adaClassify([[5, 5], [0, 0]], classifierArr))

运行结果4：

在一个难数据集上应用 AdaBoost A d a B o o s t

代码：

from ML_in_action.AdaBoost import adaBoost2
from numpy import *

# 加载数据
# 该函数不必指定每个文件中的特征数目，会自动检测特征的数目，并将最后一列作为类别标签
def loadDataSet(fileName):
    numFeat = len(open(fileName).readline().split('\t'))
    dataMat = []
    labelMat = []
    fr = open(fileName)
    for line in fr.readlines():
        lineArr = []
        curLine = line.strip().split('\t')
        for i in range(numFeat - 1):
            lineArr.append(float(curLine[i]))
        dataMat.append(lineArr)
        labelMat.append(float(curLine[-1]))
    return dataMat, labelMat

datArr, labelArr = loadDataSet('data/horseColicTraining2.txt')
classifierArr = adaBoost2.adaBoostTrainDS(datArr, labelArr, 10)

testArr, testLabelArr = loadDataSet('data/horseColicTest2.txt')
prediction10 = adaBoost2.adaClassify(testArr, classifierArr)

errArr = mat(ones((67, 1)))
print(errArr[prediction10 != mat(testLabelArr).T].sum())

运行结果5：

源代码已经数据集：

链接：https://pan.baidu.com/s/13MmA2CpTa51Vc8wdjw5twQ 密码：3o3j

参考数据：
《机器学习实战》图灵众书