【深度学习】神经网络的优化方法
前言
\quad\quad 我们都知道,神经网络的学习目的是找到使损失函数的值尽可能小的参数,这是一个寻找最优参数的问题,解决这个问题的过程可以称为最优化,但由于参数空间非常复杂,无法轻易找到最优解,而且在深度学习中,参数的数量非常大,导致最优化问题更加复杂。
\quad\quad 在这之前,我们是将参数的梯度(导数)作为线索,使参数沿着梯度方向更新,并重复执行多次,从而逐渐靠近最优参数,这个过程称为随机梯度下降法(SGD)
- 反向传播中提到了偏导数
- 误差反向传播法中应用偏导数实现了误差反向传播法,损失函数为交叉熵误差
SGD是一个简单的方法,但是比起胡乱地搜索参数空间,也算是“聪明”的方法
但是,针对不同的问题,SGD并不一定是最好的,SGD也存在自身的缺陷
下面我们介绍几种常用的最优化方法,并python实现
SGD
- 数学表达式
W ← W − η ∂ L ∂ W W \leftarrow W - \eta \frac{\partial L}{\partial W} W←W−η∂W∂L
W W W 为权重参数, η \eta η 为学习率, ∂ L ∂ W \frac{\partial L}{\partial W} ∂W∂L表示损失函数关于 W W W的梯度
一般 η \eta η 取 0.01 或 0.001
- python实现
class SGD:
"""随机梯度下降法"""
def __init__(self, lr=0.01):
self.lr = lr # 学习率
# params,grads是字典型数据,比如params['W1'],grads['W1']
# 保存了权重参数和他们的梯度
def update(self, params, grads):
for key in params.keys():
# 根据SGD公式
params[key] -= self.lr * grads[key]
- 神经网络中如何使用
# 构建网络
network = TwoLayerNet(...)
# 选择最优化方法(如果需要其他方法,可以改用其他的方法)
optimizer = SGD()
# 学习
for i in range(10000):
# 批数据
x_batch, t_batch = get_mini_batch(...)
# 求梯度
grads = network.gradient(x_batch, t_batch)
# 权重参数
params = network.params
# 优化,更新权重参数
optimizer.update(params, grads)
上面代码是进行神经网络参数更新的一般步骤,其中optimizer 就是进行参数最优化的对象
- 如果我们有了新的最优化方法,就可以创建一个和SGD类似的类,里面也包括update方法,这样只需要将上面代码中的optimizer = SGD()换成自己定义的类
- SGD的缺点
如果,梯度方向不指向最小值的方向,就会以相对低效的路径更新,出现如图的“之”型
容易收敛到局部最优,并且容易被困在鞍点
为了改正SGD的缺陷,出现了Momentum、AdaGrad、Adam等方法
Momentum
- 数学表达式
v ← α v − η ∂ L ∂ W v \leftarrow \alpha v - \eta \frac{\partial L}{\partial W} v←αv−η∂W∂L
W ← W + v W \leftarrow W + v W←W+v
这里出现了一个新变量 v v v,对应物理上的速度
式中, α v \alpha v αv 这一项表示在物体不受任何力时,该项承担物体逐渐减速的任务( α \alpha α 设定为0.9之类)
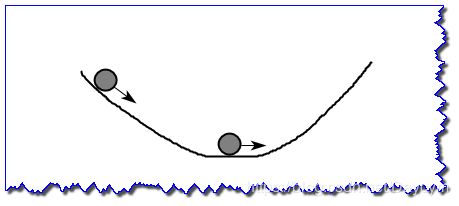
一开始,梯度为负,小球加速向下运行(梯度可以表示为加速度),并且加速度减小
当梯度为0(加速度为0),由于 v ← α v v \leftarrow \alpha v v←αv,速度逐渐减小,也就是小球还会往右边运动,这样避免陷入局部最小值
- python实现
class Momentum:
"""Momentum SGD"""
def __init__(self, lr=0.01, momentum=0.9):
self.lr = lr # 学习率
self.momentum = momentum #动量
self.v = None # 什么都不保存,第一次调用update时,会以字典形式保存与参数结构相同的数据
def update(self, params, grads):
if self.v is None:
self.v = {}
for key, val in params.items():
self.v[key] = np.zeros_like(val)
for key in params.keys():
self.v[key] = self.momentum*self.v[key] - self.lr*grads[key]
params[key] += self.v[key]
- 评价
和SGD相比,Momentum可以更快地朝最小值靠近,减弱“之”字型的变动程度
AdaGrad
在神经网络学习中,学习率的值很重要。学习率过小,会导致学习花费过多时间;学习率过大,会导致学习发散而不能正确进行
- 学习率衰减
随着学习的进行,是学习率逐渐减小,一开始“多”学,然后逐渐“少”学
上面学习率衰减是针对所有参数的,而AdaGrad是针对“每个”参数,赋予其“定制”的值,也就是每个参数的学习率不同;AdaGrad会为每个元素适当的调整学习率
- 数学表达式
h ← h + ∂ L ∂ W ⊙ ∂ L ∂ W h \leftarrow h + \frac{\partial L}{\partial W} \odot \frac{\partial L}{\partial W} h←h+∂W∂L⊙∂W∂L
W ← W − η 1 h ∂ L ∂ W W \leftarrow W - \eta \frac{1}{\sqrt h}\frac{\partial L}{\partial W} W←W−ηh1∂W∂L
⊙ \odot ⊙表示对应矩阵元素相乘,在更新参数时,通过更改 1 h \frac{1}{\sqrt h} h1就可以调整学习的尺度
这意味着,参数的元素中变化较大的元素的学习率将变小,这样就可以按参数的元素进行学习率衰减,使变动大的参数的学习率逐渐减小
- python实现
class AdaGrad:
"""AdaGrad"""
def __init__(self, lr=0.01):
self.lr = lr
self.h = None
def update(self, params, grads):
if self.h is None:
self.h = {}
for key, val in params.items():
self.h[key] = np.zeros_like(val)
for key in params.keys():
self.h[key] += grads[key] * grads[key]
params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7) # 加上1e-7为了避免有0
Adam
Adam的理论有些复杂,直观上,就是上面两种方法的结合。
-
数学表达式
m t = β 1 m t − 1 + ( 1 − β 1 ) ∂ L ∂ W m_t = \beta_1m_{t-1} + (1-\beta_1)\frac{\partial L}{\partial W} mt=β1mt−1+(1−β1)∂W∂L
v t = β 2 v t − 1 + ( 1 − β 2 ) ∂ L ∂ W ⊙ ∂ L ∂ W v_t = \beta_2v_{t-1} + (1-\beta_2)\frac{\partial L}{\partial W} \odot \frac{\partial L}{\partial W} vt=β2vt−1+(1−β2)∂W∂L⊙∂W∂L
m t ^ = m t 1 − β 1 t \hat{m_t} = \frac{m_t}{1-\beta_1^t} mt^=1−β1tmt
v t ^ = v t 1 − β 2 t \hat{v_t} = \frac{v_t}{1-\beta_2^t} vt^=1−β2tvt
W ← W − α 1 v t ^ + ϵ m t ^ W \leftarrow W - \alpha \frac{1}{\sqrt{\hat{v_t}}+\epsilon}\hat{m_t} W←W−αvt^+ϵ1mt^ -
python实现
class Adam:
"""Adam (http://arxiv.org/abs/1412.6980v8)"""
def __init__(self, lr=0.001, beta1=0.9, beta2=0.999):
self.lr = lr
self.beta1 = beta1
self.beta2 = beta2
self.iter = 0
self.m = None
self.v = None
def update(self, params, grads):
if self.m is None:
self.m, self.v = {}, {}
for key, val in params.items():
self.m[key] = np.zeros_like(val)
self.v[key] = np.zeros_like(val)
self.iter += 1
lr_t = self.lr * np.sqrt(1.0 - self.beta2**self.iter) / (1.0 - self.beta1**self.iter)
for key in params.keys():
#self.m[key] = self.beta1*self.m[key] + (1-self.beta1)*grads[key]
#self.v[key] = self.beta2*self.v[key] + (1-self.beta2)*(grads[key]**2)
self.m[key] += (1 - self.beta1) * (grads[key] - self.m[key])
self.v[key] += (1 - self.beta2) * (grads[key]**2 - self.v[key])
params[key] -= lr_t * self.m[key] / (np.sqrt(self.v[key]) + 1e-7)
#unbias_m += (1 - self.beta1) * (grads[key] - self.m[key]) # correct bias
#unbisa_b += (1 - self.beta2) * (grads[key]*grads[key] - self.v[key]) # correct bias
#params[key] += self.lr * unbias_m / (np.sqrt(unbisa_b) + 1e-7)
β 1 β_1 β1 的默认值为0.9, β 2 β_2 β2的默认值为.999, ϵ ϵ ϵ默认为10−7
此外还有,Nesterov、RMSprop,这里仅给出代码,有兴趣的可以看看:
class Nesterov:
"""Nesterov's Accelerated Gradient (http://arxiv.org/abs/1212.0901)"""
def __init__(self, lr=0.01, momentum=0.9):
self.lr = lr
self.momentum = momentum
self.v = None
def update(self, params, grads):
if self.v is None:
self.v = {}
for key, val in params.items():
self.v[key] = np.zeros_like(val)
for key in params.keys():
self.v[key] *= self.momentum
self.v[key] -= self.lr * grads[key]
params[key] += self.momentum * self.momentum * self.v[key]
params[key] -= (1 + self.momentum) * self.lr * grads[key]
class RMSprop:
"""RMSprop"""
def __init__(self, lr=0.01, decay_rate = 0.99):
self.lr = lr
self.decay_rate = decay_rate
self.h = None
def update(self, params, grads):
if self.h is None:
self.h = {}
for key, val in params.items():
self.h[key] = np.zeros_like(val)
for key in params.keys():
self.h[key] *= self.decay_rate
self.h[key] += (1 - self.decay_rate) * grads[key] * grads[key]
params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7)
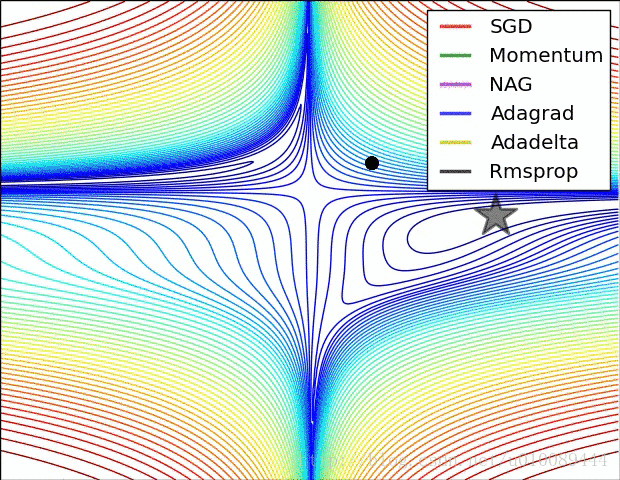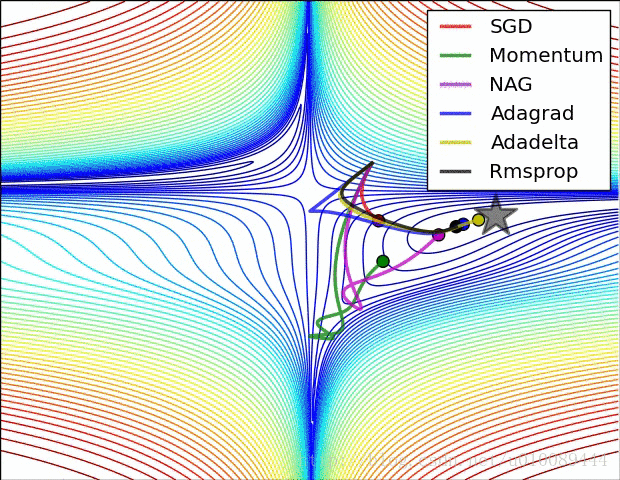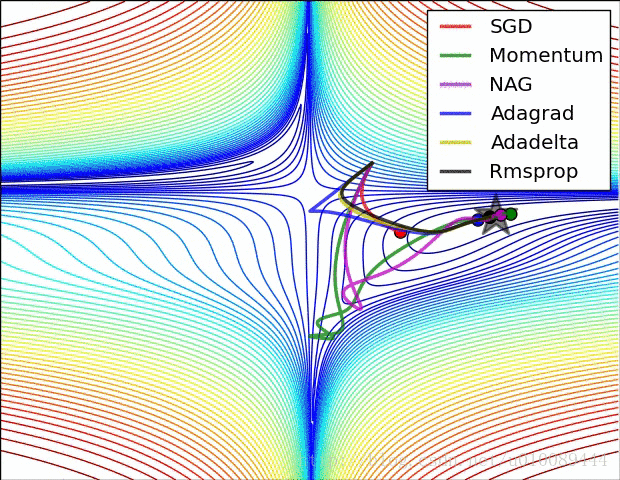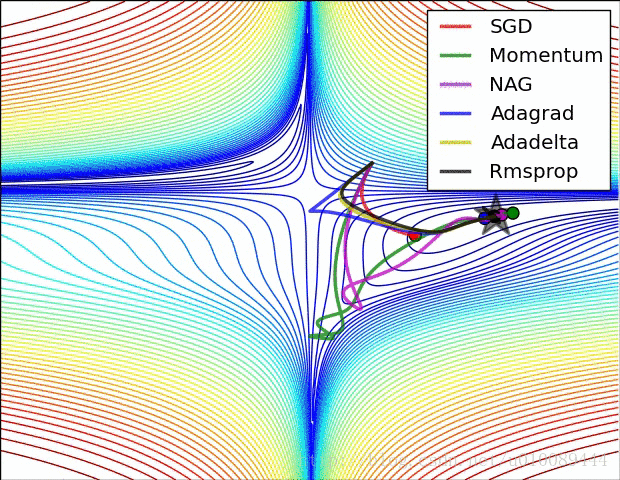
分析
第一张图为不同算法在损失平面等高线上随时间的变化情况,第二张图为不同算法在鞍点处的行为比较。
图片来自优化方法总结:SGD,Momentum,AdaGrad,RMSProp,Adam
其中也包含了公式,可参考