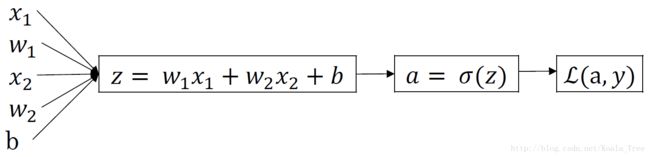神经网络基础--DeepLearning.ai 学习笔记(1-2)
课程笔记地址:https://blog.csdn.net/column/details/26931.html
课程代码地址:https://github.com/duboya/DeepLearning.ai-pragramming-code/tree/master
欢迎大家fork及star!(-O-)
神经网络和深度学习—神经网络基础
1.二分类问题
对于二分类问题,Ng给出了小的Notation。
- 样本:(x,y),训练样本包含m个;
- 其中 x ∈ R n x x \in R^{n_x} x∈Rnx,表示样本x包含 n x n_x nx个特征;
- y ∈ 0 , 1 y \in 0,1 y∈0,1,目标值属于0,1分类;
- 训练样本数据: { ( x ( 1 ) , y ( 1 ) ) , ( x ( 2 ) , y ( 2 ) ) , . . . , ( x ( m ) , y ( m ) ) } \{(x^{(1)},y^{(1)}), (x^{(2)},y^{(2)}), ... ,(x^{(m)},y^{(m)}) \} {(x(1),y(1)),(x(2),y(2)),...,(x(m),y(m))};
- X.shape = ( n x n_x nx, m)
- 目标数据的形状:
Y = [ y ( 1 ) , y ( 2 ) , . . . , y ( m ) y^{(1)}, y^{(2)}, ..., y^{(m)} y(1),y(2),...,y(m)]
Y.shape = (1,m)
2. logistic Regression
逻辑回归中,预测值:
h ^ = P ( y = 1 ∣ x ) \hat{h} = P(y=1|x) h^=P(y=1∣x)
其表示为1的概率,取值范围在 [ 0 , 1 ] [0,1] [0,1]之间。
引入Sigmoid函数,预测值:
y ^ = S i g m o i d ( w T x + b ) = σ ( w T x + b ) \hat{y} = Sigmoid(w^Tx+b) = \sigma(w^Tx+b) y^=Sigmoid(wTx+b)=σ(wTx+b)
其中:
S i g m o i d ( z ) = 1 1 + e − z Sigmoid(z) = \frac{1}{1+e^{-z}} Sigmoid(z)=1+e−z1
注意点: 函数的一阶导数可以用自身表示:
σ ′ ( z ) = σ ( z ) ( 1 − σ ( z ) ) \sigma\prime{(z)} = \sigma(z)(1 - \sigma(z)) σ′(z)=σ(z)(1−σ(z))
这里可以解释梯度消失的问题,当 z=0 时候,导数最大,但是导数最大为 σ ′ ( 0 ) = σ ( 0 ) ( 1 − σ ( 0 ) ) = 0.5 ( 1 − 0.5 ) = 0.25 \sigma\prime{(0)} = \sigma(0)(1 - \sigma(0)) = 0.5(1 - 0.5) = 0.25 σ′(0)=σ(0)(1−σ(0))=0.5(1−0.5)=0.25,这里导数仅为原函数值的0.25倍。
参数梯度下降公式的不断更新, σ ′ ( z ) \sigma\prime{(z)} σ′(z)会变得越来越小,每次迭代参数更新的步伐越来越小,最终接近于0,产生梯度消失的现象。
3. logistic Regression loss function
Loss function
一般经验来说,使用均方误差(squared error)来衡量Loss Function:
L ( y ^ , y ) = 1 2 ( y ^ − y ) 2 L(\hat{y}, y)=\frac{1}{2}(\hat{y} − y)^2 L(y^,y)=21(y^−y)2
但是,对于logistic regression 来说,一般不适用squared error来作为Loss Function,这是因为上面的均方误差损失函数一般是非凸函数(non-convex),其在低纬空间下降收敛的时候,容易得到局部最优解,而不是全局最优解,因此要选择凸函数。
注:高维空间中往往无需考虑极值点是不是最值点的问题。
一是实际工程显示出,即便最后方程只是收敛到极值点,所带来的误差也很小,已经满足工程需求,对于大多数场景,花费更多计算成本寻找最值点在工程中并不是一种很好的解决方案。
二是在高维空间中如N维空间中,若想找到极值点的概率是 p N p^N pN,维度越大,概率越小,这种情况近似可以忽略。在高维空间中更多时候找到的是一种鞍点,但也有很多方法可以跳出鞍点,如以后Ng会介绍的Adam、momentum等。
逻辑回归的Loss Function:
L ( y ^ , y ) = − ( y l o g y ^ + ( 1 − y ) l o g ( 1 − y ^ ) ) L(\hat{y}, y) = -(ylog\hat{y} + (1 -y)log(1 - \hat{y})) L(y^,y)=−(ylogy^+(1−y)log(1−y^))
-
当 y=1 时, L ( y ^ , y ) = − l o g y ^ L(\hat{y}, y) = -log{\hat{y}} L(y^,y)=−logy^。如果 y ^ \hat{y} y^越接近1, L ( y ^ , y ) ≈ 0 L(\hat{y}, y) \approx 0 L(y^,y)≈0,表示预测效果越好;如果 y ^ \hat{y} y^越接近0, L ( y ^ , y ) ≈ + ∞ L(\hat{y}, y) \approx +\infty L(y^,y)≈+∞,表示预测效果越差;
-
当 y=0 时, L ( y ^ , y ) = − l o g ( 1 − y ^ ) L(\hat{y}, y) = -log(1 - \hat{y}) L(y^,y)=−log(1−y^)。如果 y ^ \hat{y} y^越接近0, L ( y ^ , y ) ≈ 0 L(\hat{y}, y) \approx 0 L(y^,y)≈0,表示预测效果越好;如果 y ^ \hat{y} y^越接近1, L ( y ^ , y ) ≈ + ∞ L(\hat{y}, y) \approx +\infty L(y^,y)≈+∞,表示预测效果越差;
-
我们的目标是最小化样本点的损失Loss Function,损失函数是针对单个样本点的。
Cost function
全部训练数据集的Loss function综合的平均值即为训练集的代价函数(cost function):
J ( w , b ) = 1 m ∑ i = 1 m L ( y ^ ( i ) , y ( i ) ) = − 1 m ∑ i = 1 m [ y ( i ) l o g y ^ ( i ) + ( 1 − y ( i ) ) l o g ( 1 − y ^ ( i ) ) ] J(w,b) = \frac{1}{m}\sum_{i=1}^{m}L(\hat{y}^{(i)}, y^{(i)}) \\ = -\frac{1}{m}\sum_{i=1}^{m}[y^{(i)}log \hat{y}^{(i)} + (1 - y^{(i)}) log(1 - \hat{y}^{(i)})] J(w,b)=m1i=1∑mL(y^(i),y(i))=−m1i=1∑m[y(i)logy^(i)+(1−y(i))log(1−y^(i))]
- Cost function 是待求系数 w 和 b 的函数;
- 我们的目标就是迭代计算出最佳的 w 和 b 的值,最小化Cost function,让其尽可能地接近于0;
4. gradient descent
用梯度下降法(Gradient Descent)算法来最小化Cost function,以计算出最合适的 w 和 b 的值。
每次迭代更新的修正表达式:
w : = w − α ∂ J ( w , b ) ∂ w w : = w - \alpha\frac{\partial J(w,b)}{\partial w} w:=w−α∂w∂J(w,b)
b : = b − α ∂ J ( w , b ) ∂ b b : = b - \alpha\frac{\partial J(w,b)}{\partial b} b:=b−α∂b∂J(w,b)
在程序代码中,我们通常使用 dw 来表示 ∂ J ( w , b ) ∂ w \frac{\partial J(w,b)}{\partial w} ∂w∂J(w,b),用db来表示 ∂ J ( w , b ) ∂ b \frac{\partial J(w,b)}{\partial b} ∂b∂J(w,b) 。
5. gradient descent of logistic regression
对的那个样本而言,逻辑回归Loss function表达式:
z = w T x + b y ^ = a = σ ( z ) z = w^Tx+b\\ \hat{y} = a = \sigma(z) z=wTx+by^=a=σ(z)
L ( a , y ) = − ( y l o g ( a ) + ( 1 − y ) l o g ( 1 − a ) ) L(a,y) = -(ylog(a) + (1-y)log(1-a)) L(a,y)=−(ylog(a)+(1−y)log(1−a))
6. m个样本的梯度下降
前面过程的dz, dz求导:
d a = ∂ L ∂ a = − y a + 1 − y 1 − a da = \frac{\partial{L}}{\partial{a}} = -\frac{y}{a} + \frac{1-y}{1-a} \\ da=∂a∂L=−ay+1−a1−y
d z = ∂ L ∂ z = ∂ L ∂ a ⋅ ∂ a ∂ z = ( − y a + 1 − y 1 − a ) ⋅ a ( 1 − a ) = a − y dz = \frac{\partial{L}}{\partial{z}} = \frac{\partial{L}}{\partial{a}} \cdot \frac{\partial{a}}{\partial{z}} = (-\frac{y}{a} + \frac{1-y}{1-a}) \cdot a(1-a) = a- y dz=∂z∂L=∂a∂L⋅∂z∂a=(−ay+1−a1−y)⋅a(1−a)=a−y
再对 w 1 w_1 w1, w 2 w_2 w2 和 b b b 进行求导:
d w 1 = ∂ L ∂ w 1 = ∂ L ∂ z ⋅ ∂ z ∂ w 1 = x 1 ⋅ d z = x 1 ( a − y ) dw_1 = \frac{\partial{L}}{\partial{w_1}} = \frac{\partial{L}}{\partial{z}} \cdot \frac{\partial{z}}{\partial{w_1}} = x_1 \cdot dz = x_1 (a-y) dw1=∂w1∂L=∂z∂L⋅∂w1∂z=x1⋅dz=x1(a−y)
d b = ∂ L ∂ b = ∂ L ∂ z ⋅ ∂ z ∂ b = 1 ⋅ d z = a − y db = \frac{\partial{L}}{\partial{b}} = \frac{\partial{L}}{\partial{z}} \cdot \frac{\partial{z}}{\partial{b}} = 1 \cdot dz = a-y db=∂b∂L=∂z∂L⋅∂b∂z=1⋅dz=a−y
梯度下降法:
w 1 : = w 1 − α d w 1 w 2 : = w 2 − α d w 2 b : = b − α d b w_1 := w_1 - \alpha dw1 \\ w_2 := w_2 - \alpha dw2 \\ b := b - \alpha db w1:=w1−αdw1w2:=w2−αdw2b:=b−αdb
7. 向量化(vectorization)
在深度学习的算法中,我们通常拥有大量的数据,在程序的编写过程中,应该尽最大可能的少使用loop循环语句,利用python可以实现矩阵运算,进而来提高程序的运行速度,避免for循环的使用。
逻辑回归向量化
- 输入矩阵 X X X: ( n x , m ) (n_x, m) (nx,m)
- 权重矩阵 w w w: ( n x , 1 ) (n_x, 1) (nx,1)
- 偏执 b b b: 为一个常数
- 输出矩阵 Y Y Y: ( 1 , m ) (1, m) (1,m)
所有 m 个样本的线性输出Z可以用矩阵表示:
Z = w T X + b Z = w^T X + b Z=wTX+b
Python 代码:
Z = np.dot(w.T, X) + b
A = sigmoid(Z)
逻辑回归梯度下降输出向量化:
- dZ 对于m个样本,维度为 (1, m),表示为:
d Z = A − Y dZ = A - Y dZ=A−Y - db 可以表示为:
d b = 1 m ∑ i = 1 m d Z ( i ) db = \frac{1}{m}\sum_{i=1}^{m}dZ^{(i)} db=m1i=1∑mdZ(i)
Python 代码:
db = 1/m * np.sum(dZ)
- dw 可表示为:
d w = 1 m X ⋅ d Z T dw = \frac{1}{m}X \cdot dZ^T dw=m1X⋅dZT
Python 代码为:
dw = 1/m * np.dot(X, dZ.T)
单次迭代梯度下降算法流程
Z = np.dot(w.T,X) + b
A = sigmoid(Z)
dZ = A-Y
dw = 1/m*np.dot(X,dZ.T)
db = 1/m*np.sum(dZ)
w = w - alpha*dw
b = b - alpha*db
8. python的notation
-
虽然在Python有广播的机制,但是在Python程序中,为了保证矩阵运算的正确性,可以使用reshape()函数来对矩阵设定所需要进行计算的维度,这是个好的习惯;
-
如果用下列语句来定义一个向量,则这条语句生成的a的维度为(5,),既不是行向量也不是列向量,称为秩(rank)为1的array,如果对a进行转置,则会得到a本身,这在计算中会给我们带来一些问题。
a = np.random.randn(5)
- 如果需要定义(5,1)或者(1,5)向量,要使用下面标准的语句:
a = np.random.randn(5,1)
b = np.random.randn(1,5)
- 可以使用assert语句对向量或数组的维度进行判断。assert会对内嵌语句进行判断,即判断a的维度是不是(5,1),如果不是,则程序在此处停止。使用assert语句也是一种很好的习惯,能够帮助我们及时检查、发现语句是否正确。
assert(a.shape == (5,1))
- 可以使用reshape函数对数组设定所需的维度
a.reshape((5,1))
注:参考补充自:
https://blog.csdn.net/koala_tree/article/details/78045596