PyTorch学习3—神经网络

引言
按照惯例，先说明一下我的英语水平不高，翻译效果难免捉急。所以觉得语句不通的话，别太激动。。。原文地址：Neural Networks

神经网络
用 torch.nn 包可以构建神经网络。

现在你对 autograd 有了初步认识了， nn包 依赖于 autograd 包去定义模型和区分它们。 nn.Module 包含了层，和一个返回 output 的 forward(input) 方法。

例如，看看下面这个给数码图分类的网络：

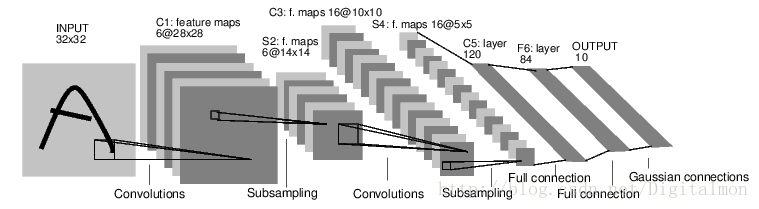
这是一个简单的前馈网络。它接受输入，通过一层又一层的网络层来进行反馈，最后得到输出（这句话的翻译好迷）。

一个典型的神经网络的训练程序如下：

• 定义一个拥有一些可以通过学习而改变的参数（或权重）
• 迭代地将数据集输入
• 通过网络进行进程输入
• 计算损失（输出的结果与正确结果之间的距离有多大）
• 反向传播梯度来改变网络的参数
• 更新网络的权重，（典型地）使用一个简单的更新方法： weight = weight - learning_rate * gradient

定义网络
让我们来定义如下网络：

import torch
from torch.autograd import Variable
import torch.nn as nn
import torch.nn.functional as F

class Net(nn.Module):
    def __init__(self):
        super(Net,self).__init__()
        # 1个作为输入的图像通道，6个作为输出的通道，5*5的正方卷积
        # 内核
        self.conv1 = nn.Conv2d(1,6,5)
        self.conv2 = nn.Conv2d(6,16,5)
        # 一个仿射运算：y = wx + b
        self.fc1 = nn.Linear(16*5*5,120)
        self.fc2 = nn.Linear(120,84)
        self.fc3 = nn.Linear(84,10)

    def forward(self,x):
        # 用一个（2，2）的窗口进行max pooling
        x = F.max_pool2d(F.relu(self.conv1(x)),(2,2))
        # 如果尺寸是一个正方形，你只能识别出一个单独的数字
        x = F.max_pool2d(F.relu(self.conv2(x)), 2)
        x = x.view(-1, self.num_flat_features(x))
        x = F.relu(self.fc1(x))
        x = F.relu(self.fc2(x))
        x = self.fc3(x)
        return x

    def num_flat_features(self,x):
        size = x.size()[1: ] # 所有维度（除了batch维度）
        num_features = 1
        for s in size:
            num_features *= s
        return num_features 

net = Net()
print(net)

输出：

Net (
  (conv1): Conv2d(1, 6, kernel_size=(5, 5), stride=(1, 1))
  (conv2): Conv2d(6, 16, kernel_size=(5, 5), stride=(1, 1))
  (fc1): Linear (400 -> 120)
  (fc2): Linear (120 -> 84)
  (fc3): Linear (84 -> 10)
)

你只需要定义 forward ， backward 函数（梯度在这个函数里计算）就会通过 autograd 给你自动定义好。你可以用 forward 函数进行任何对张量的操作。

net.parameters() 返回可学习的参数的模型

params = list(net.parameters())
print(len(params))
print(params[0].size())  # conv1's .weight

输出：

10
torch.Size([6, 1, 5, 5])

向前端的输入是一个 autograd.Variable ，输出也是（这句话太简明了点吧……）

input = Variable(torch.randn(1, 1, 32, 32))
out = net(input)
print(out)

输出：

Variable containing:
 0.0184 -0.0314 -0.1252  0.0939  0.0179  0.1218  0.0024  0.0724 -0.1241 -0.1183
[torch.FloatTensor of size 1x10]

Zero the gradient buffers of all parameters and backprops with random gradients. （这句实在是翻译不能）

net.zero_grad()
out.backward(torch.randn(1, 10))

torch.nn 只支持 mini-batches。整个 torch.nn 包只支持分批处理的样例，而不是一个一次抽样样例。

例如， nn.Conv2d 会包含一个 nSamples x nChannels x Height x Width 的4D张量

如果你有一个一次抽样的样例，只需使用 input.unsqueeze(0) 去增加一个批次维度。

重点知识梳理：

• torch.Tensor 一个多维数组
• autograd.Variable 封装一个张量，并且记录对此张量进行操作的历史。拥有与 Tensor 相同的API，还有一些像 backward() 的额外功能。并且保存关于张量的梯度。
• nn.Moudle 神经网络模型。在输出或加载等的时候，将参数转移到GPU，有利于他们封装的便利性。
• nn.Parameter 一种变量，当被分配成 Module 的一个属性时，它被自动地注册成一个参数。
• autograd.Function 一个定义autograd向前和向后操作的声明。对每个 Variable 的操作，创建至少一个单独的 Function 节点，这个（些）节点与创建 Variable 的函数相连接，并且以编码的形式记录节点的历史。

在这里，我们讲了：

• 定义一个神经网络
• 处理输入并向进行反馈

还有以下未讲：

• 计算损失函数
• 更新神经网络的权重值

损失函数
损失函数的输入为（原网络的输出，正确值）的数值对，它计算神经网络的输出距离正确值有多远。

在 nn 包里有几种不同的损失函数。一个简单的例子是 nn.MSELoss ，这个函数计算神经网络输出值与正确值（目标值）的均方差（mean-squared error）。

For example:

output = net(input)
target = Variable(torch.arange(1, 11))  # 在这里假设一个目标值来举例子
criterion = nn.MSELoss()

loss = criterion(output, target)
print(loss)

输出：

Variable containing:
 38.6931
[torch.FloatTensor of size 1]

现在，如果你在反馈的方向上跟着 loss 函数，使用它的 .grad_fn 属性，你可以看到一个类似下面的计算图：

input -> conv2d -> relu -> maxpool2d -> conv2d -> relu -> maxpool2d
      -> view -> linear -> relu -> linear -> relu -> linear
      -> MSELoss
      -> loss

因此，当我们使用 loss.backward() 时，整个图会随着损失值而变化，并且图中的所有变量会伴随着梯度而累积着它们的 .grad 属性。

例如，让我们向后走几步：

print(loss.grad_fn)  # MSELoss
print(loss.grad_fn.next_functions[0][0])  # Linear 
print(loss.grad_fn.next_functions[0][0].next_functions[0][0])  # ReLU 

输出：

object at 0x7fbe08423048>
object at 0x7fbe08410e58>
object at 0x7fbe08403400>

反向传播（BP）

为了对错误（误差）进行梯度反向传递，我们要做的就是使用 loss.backward() 函数。你需要清除现有的梯度，否则梯度就会累积到现有的梯度。

现在我们看一下 loss.backward() ，并且看一下 conv1 在反向传递前后的梯度偏移变化。

net.zero_grad()     # zeroes the gradient buffers of all parameters（各个参数零点的缓冲区）

print('conv1.bias.grad before backward')
print(net.conv1.bias.grad)

loss.backward()

print('conv1.bias.grad after backward')
print(net.conv1.bias.grad)

输出：

conv1.bias.grad before backward
Variable containing:
 0
 0
 0
 0
 0
 0
[torch.FloatTensor of size 6]

conv1.bias.grad after backward
Variable containing:
1.00000e-02 *
  1.9986
 -1.7405
  2.1624
 -0.4565
 -3.3579
  1.2404
[torch.FloatTensor of size 6]

现在，我们来看一下如何使用损失函数。

稍后阅读：
神经网络专用包包含了多种多样的组建深度神经网络的网络模型和损失函数。一个详细周全的文档链接：here !

现在还剩下的是：更新神经网络的权重值

更新权重

最简单的更新方法是使用随机梯度下降法（Stochastic Gradient Descent ，SGD)：

weight = weight - learning_rate * gradient

我们可以使用如下简单的python代码来实现它：

learning_rate = 0.01
for f in net.parameters():
    f.data.sub_(f.grad.data * learning_rate)

然而，当你操作神经网络时，你会去想使用其他花样更多点的更新方法，比如说：SGD, Nesterov-SGD, Adam, RMSProp，等。 torch 里有一个小包， torch.optim ，它实现了包括上述列举方法在内的各种更新权重的方法。使用这个包很简单：

import torch.optim as optim

# create your optimizer（创建你的优化器）
optimizer = optim.SGD(net.parameters(), lr=0.01)

# in your training loop（在你的训练环里）
optimizer.zero_grad()   # zero the gradient buffers（缓冲区置零）
output = net(input)
loss = criterion(output, target)
loss.backward()
optimizer.step()    # Does the update（进行更新）

At last:
终于翻译完了。鉴于本人凭运气飘过六级及格线的英语水平以及刚刚接触深度学习的零基础功底，翻译的毛病还有很多，请多见谅。。。
（.grad_fn 属性运行不了的话，就用.creator 属性代替）