cs229 斯坦福机器学习笔记（二）-- LR回顾与svm算法idea理解

LR回顾

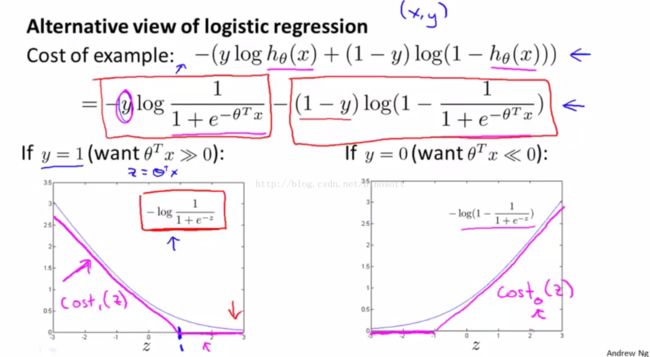
LR是机器学习入门的第一道坎，总结一下，Linear Regression 和logistic Regression都是属于GLM，套了logistic之后，输出结果就变成一个概率了，loss function和 likelihood function取反是类似的东西，都可以作为优化的目标。但我感觉  likelihood function从概率统计上来说，更有理论支持吧。loss function 直接对残差求平方和，直觉上也是挺合理的；当然，对于logistic Regression来说，概率值求残差就说不太通了，更重要的原因是非凸函数，不好求解。

coursera ml的编程题文档确实不错，非常细致，导致后来视频没怎么看就直接把题目下下来做掉了。动手还是挺重要的，比干看理论能有更深入的体会。做完编程题，印像最深刻的就是w0的处理了，正则化的时候要排除掉它。这东西叫bias，或者叫intercept term啥的。因为这个东西，搞得处理起来还挺麻烦的。举个简单情况 y= w１ * x +　ｗ０，这里w0就是一个截距，调节直线不穿过原点。从这个角度想想，w0确实不应该正则化，值是多少就多少。

Note that often the coefficient w0 is omitted from the regularizer because its
inclusion causes the results to depend on the choice of origin for the target variable
(Hastie et al., 2001), or it may be included but with its own regularization coefficient
(we shall discuss this topic in more detail in Section 5.5.1).

prml提到两点。应该好理解，意思就是说你可以选择线性变换一下y，或者单独给w0选择一个正则化的系数。

另外一个问题，就是工作中，我们提到的LR模型到底是指Linear Regression 还是 Logistic Regression？一般是指后者，主要用来做ctr（pv /ctr）预估之类的工作，结果可以直接作为一个分数来用，其实就是一个2分类的问题，点击，或者不点击。LR有意思的一点就是如果对“发生比”（odd，发生的概率除以不发生的概率）取自然对数，结果w*x，是线性的。（可以看看李航的《统计学习方法》）

另外一个问题就是正则项了，正则项就是防止over fitting的一个东西。别人口中的L1正则L2正则到底是什么鬼？ L1容易产生稀疏解倒是什么一回事？这个正则项从概率统计来说，属于贝叶斯规则化方法（“我们将高斯先验概率引入到参数中计算MAP（极大后验）估计（而不是极大似然估计）”，在ufldl看到这句话，然后google了一下，找到这篇知乎回答 http://www.zhihu.com/question/20700829  可以看看 ）。

后来看scikit-learn文档的时候，发现了一些新名词，吓得我菊花一紧，以为还有好多算法得学。原来只是换了个马甲而已。

L2 regularization -> ridge 

L1 regularization ->  lasso

mix L1 and L2  -> elastic Net

LR是线性模型。线性是个很好的特性，但也是假设比较强的特性。不过线性是对于权重来说，并不是对于输入，也就是说y=w *ｘ^2 + b 也是线性的。实践中用LR模型，拟合非线性，通常就是用离散化和特征组合。

离散化：比方说，两个学生高考，一个考98，一个考95，从分数上是有区别，但从能力上不见得有特别大的不同，算得太细反而不准确。我们可以把分数离散化成A、B、C、D四个等级，然后用４个二进制特征编码，比如Ａ＝０００1，Ｂ＝0 0 1 0 。又比方年龄18 +啥的，现实中就是这样来分级，只需要级别，具体的数值倒不是人们的关注点。

特征组合：数值特征跟id特征组合一番。比如query类目男装=0，1，女装=1，0。用户购买力=x，用户等级=y，求个笛卡尔积，就能得到4个特征。<购买力, 男装类目> <购买力, 女装类目> <用户等级,男装类目> <用户等级,女装类目>。靠这样的拟合非线性，其实就是补充特征的“AND”关系。

开始svm

第二个坎就是svm。不过说svm难，其实还是数学求解过程有些难。如果先学了convex optimization（session notes有 精简版的cs229-cvxopt.pdf和cs229-cvxopt2.pdf，挺不错的。单单从内容本身来讲，是要先看这两个再看svm，不过实际上，我觉得这么枯燥的东西比较难看下去，可能先看svm，被里面的对偶折腾得半死的时候，才有兴趣看看凸优化，两个资料最好叉看吧）这门课，估计一下子就秒杀了。不过学一个算法，主要还是要理解算法的idea。我一开始拘泥于数学的推导和求解，结果就踩坑了。svm的思想其实很简单，就是找离边界最近的点，然后从中选出可以使间隔最大的。

对比一下LR。svm关注点更多放在分类边界（更准确的说，就是那些support vectors），而LR考虑的是全部样本。这让我想起photoshop里面的一个查找边缘滤镜。仔细想想，对于分类来说，我们是不是更关注边界的地方？离边界太远的点我们关心么？

用数学语言来描述，就是svm的loss function是higne loss http://en.wikipedia.org/wiki/Hinge_loss 罢了，

svm其实就这么简单！

l(y) = max ( 0, 1 - t*y ) 。

一个神奇的max操作，就把离边界太远的点丢掉了（loss=0了，直接丢掉）。

所以cs229的课件，svm看得我蛋疼菊紧，coursera的课程居然就简单地画了个图。 

虽然从图片上看是差不多，但从计算上看，为了去掉那些离边界过远的点，还要用拉格朗日对偶，搞得有点麻烦的。

或者，我们可以从另外一个角度来理解svm。svm训练完的模型也是wTx + b，

而其中

我们可以理解为为每个样本x(i)，我们分配了一个αi来指示x(i)到底是不是support vector，通过不断迭代，那些远离边界的点慢慢 αi就变成0了。同时，我们也可以发现wTx其实就是support vector的span（线性生成空间）。另外，对比LR，假设xi ∈ R2，我们学出来的模型只有w0，w1，w2三个参数，而svm参数个数是support vector的α个数，可以远远多于2个，形成比LR跟复杂的模型。

对比LR，正则化项C=1/λ

模型结果，LR输出w，svm的w=∑alphas_i * yi * xi，如果你要用核函数的话，还得把xi带上，不能只保存w。

简单小结一下：

• svm  关注边界，丢掉离边界太远的点。输入精度低了，输出也一般只输出分类-1或1
• LR 考虑全部点，输出概率（较精细）

动手实践svm

我之前买了一本《机器学习实战》，我也觉得用里面的代码来学着实现一下svm还是比较不错的。

分类战车有个总结的不错，用的就是《机器学习实战》的例子，代码实现过程中，有些式子还要简单推导一下，里面指点一下，一下子就脑洞大开了，一开始还没搞清楚。

【分类战车SVM】这个系列终于写完了，第一话：开题话http://t.cn/RAl1Qou；第二话：线性分类http://t.cn/RAl1QoT；第三话：拉格朗日对偶http://t.cn/RAl1Qom；第四话：核函数http://t.cn/RAl1QoE；第五话：SMOhttp://t.cn/RAl1Qon；第六话：编程http://t.cn/RAl1QoQ；附录：http://t.cn/RAl1QoR

如果要实现svm，拉格朗日对偶，kkt啥的还是得老老实实搞懂才行的。我以前觉得不完全搞懂，看着伪代码自己实现一下svm没多大意思。结果自己动手写了下，还是有些体会的。 《机器学习实战》用的python实现，做了coursera的课程编程作业后，感觉用octave写起来更顺一点，代码比较贴近公式。

function model=svm(X, y, C, max_iter, Kernel)

y( y==0 ) = -1;
%m: # of sample
%n: # of feature dimension
[m,n] = size(X);
alphas = zeros(m,1);
b=0;
toler=1e-3;
K = zeros(m);
for i = 1:m
    for j = i:m
         K(i,j) = Kernel(X(i,:)', X(j,:)');
         K(j,i) = K(i,j); %the matrix is symmetric
    end
end
iter = 0;

while  iter  < max_iter
	alphaPairsChanged = 0;
	for i = 1:m
		fXi = f (alphas, y, X, b , i, K);
		Ei = fXi - y(i);
		
		if ( y(i) * Ei < -toler   & alphas(i) < C   ) ...
			|| (  y(i)* Ei > toler   &  alphas(i) > 0 ) 
			j = randSelectJ ( i, m );
			#j = mod(i + 1 , m ) + 1;
			fXj = f (alphas, y, X, b , j, K); 
			Ej = fXj - y(j);
			alpha_i_old = alphas(i);
			alpha_j_old = alphas(j);

			if ( y(i) ~= y(j) ) 
				L=max( 0, alphas(j) -alphas(i) );
				H=min( C, C + alphas(j) -alphas(i) );
			else
				L=max(0, alphas(j) + alphas(i) - C);
				H=min(C, alphas(j) + alphas(i) );
			end
			if L == H 
				fprintf("L==H!\n");
				continue;
			end
			eta = 2 * K(i,j ) - K(i,i) - K(j, j);
			if  ( eta >= 0 ) 
				fprintf("eta>=0\n");
				continue;
			end
			alphas(j) -= y(j) * (Ei -Ej) /eta;
			tmp_j= clipAlpha( alphas(j), H, L );
      alphas(j) = tmp_j;
      
			if ( abs( alphas(j) - alpha_j_old ) < 0.00001 ) 
				continue;
			end
			alphas(i) += y(j) * y(i) * (alpha_j_old - alphas(j) );
			
			b1 = b - Ei - y(i) * ( alphas(i) - alpha_i_old) * K( i, i ) ...
			     - y(j) * ( alphas(j) - alpha_j_old ) * K( i, j );
			b2 = b - Ej - y(i) * ( alphas(i) - alpha_i_old) * K( i, j  ) ...
			     - y(j) * ( alphas(j) - alpha_j_old ) * K( j, j );
			if ( 0 < alphas(i) ) & ( C > alphas(i) ) 
				b = b1;
			elseif ( 0 < alphas(j) ) & ( C > alphas(j) )
			    b = b2;
			else
				b = (b1+b2)/2;
			end
			alphaPairsChanged += 1;
			fprintf("iter: %d,  i:%d, pairs changed %d\n", iter, i, alphaPairsChanged);
			if exist('OCTAVE_VERSION')
				fflush(stdout);
			end
        
		end		%END OF IF

	end  %END OF FOR

    if alphaPairsChanged == 0 
	  iter += 1;
	else 
	  iter =0;
	end

    fprintf( "iteration number : %d\n", iter);
end  
idx = alphas > 0;
model.idx=idx;
model.X= X(idx,:);
model.y= y(idx);
model.kernelFunction = Kernel;
model.b= b;
model.alphas= alphas(idx);
model.w = ((alphas.*y)'*X)';
end

体会：

svm	LR
模型还包含原始的X,y（当然，只要存support vector的，如果不用kernel，那也可以直接求最后的w）	只需要w
y取值{-1，1}，当然，只是为了计算方便。不过实现的时候还是踩到坑，没有发现随便拿来的数据里面y居然是{ 0,1 } 的。打印调试信息才恍然大悟。	y取值 { 0，1 }

我最开始的时候觉得svm牛B是因为可以用kernel。那kernel 是svm专属的么？　不是。　那LR为啥不用kernel？　《 龙星机器学习》视频里说是求解效率不高。暂时也不求甚解了。