【模板】可持久化数组

戳我

可持久化数组是由可持久化线段树或可持久化平衡树实现的。这里先给出可持久化线段树的实现方法。

为了方便起见，处理的数组长度为5， 起始的数组元素为1~5，修改是将第一个位置的数组元素改为2。
建树规则很简单，只要在叶子节点上写上该点的值就可以了。

先根据原数组建一棵线段树

第一次修改之后的线段树

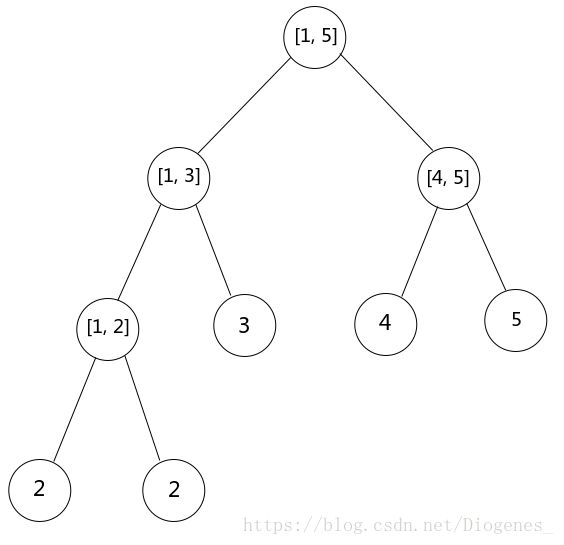
我们发现，这两棵线段树中只有一个叶子节点的值发生了改变，而操作数非常多，假如每次都memset一下，然后修改一个值，空间上的巨大开销几乎无法想象，那我们可以设想一下，把两个线段树“合并一下”……

把两次线段树合并的结果

这下我们的思路就很清楚了。每次对某个历史版本进行修改时，对于所有包含该位置的区间结点全部新开一个，并与其父节点连边，对于其他结点，由于不需要发生改动，所以直接连接即可。

Code C o d e

#include  
#include  
#include  
#include 
#include 
#define maxn 2000005
int n, m, p, x, y, lastans;  
int a[maxn];
inline int getint() {
    int num = 0, sign = 1;
    char ch = getchar();
    while (ch < '0' || ch > '9') {
        ch == '-' ? sign = -1 : 1;
        ch = getchar();
    }
    while (ch >= '0' && ch <= '9') 
        num = (num << 3) + (num << 1) + (ch ^ '0'),
        ch = getchar();
    return num * sign;
}
struct Rope { //想不出有什么好名字，，由于c++STL中有支持可持久化的数组rope，就把名字搬过来了。
    static const int MAXSIZE = 2000005;
    int cnt, value[MAXSIZE << 4];
    int root[MAXSIZE << 4], lc[MAXSIZE << 4], rc[MAXSIZE << 4];
    void build(int &k, int l, int r) {  //build
        k = ++cnt;  //由于结点数目并不固定，采取数组模拟链表而不是类似堆的存储方式存储一棵线段树
        if (l == r) {
            value[k] = a[l];
            return;
        }  
        int mid = (l + r) >> 1;  
        build(lc[k], l, mid);
        build(rc[k], mid + 1, r);  
    }  
    int query(int k, int l, int r, int pos) {  
        if (l == r) return value[k];  
        int mid = (l + r) >> 1;  
        if (pos <= mid) 
            return query(lc[k], l, mid, pos);  
        else return query(rc[k], mid + 1, r, pos);  
    }  
    void insert(int x, int &y, int l, int r, int pos, int val) {  
        y = ++cnt;  
        if (l == r) {
            value[y] = val;
            return;
        }  
        int mid = (l + r) >> 1;  
        lc[y] = lc[x]; rc[y] = rc[x];  //复制左子树和右子树，那些需要重开的结点会在接下来的递归被修改
        if (pos <= mid) 
            insert(lc[x], lc[y], l, mid, pos, val);  
        else insert(rc[x], rc[y], mid + 1, r, pos, val);  
    }  
    void build(int l, int r) { //build函数重载，主程序中调用
        build(root[0], l, r);
    }
    int find(int x, int y, int z) {  //find重载
        root[z] = root[x];
        return query(root[x], 1, n, y);   
    }  
    void insert(int x, int y, int pos, int val) { //insert重载
        insert(root[x], root[y], 1, n, pos, val);
    }
};
Rope array;
int main() {  
    n = getint(); m = getint();  
    for (int i = 1; i <= n; i++)
        a[i] = getint();
    array.build(1, n);  
    for(int i = 1; i <= m; i++) {  
        int x = getint(), opt = getint(), y = getint();  
        if (opt == 1) 
            array.insert(x, i, y, getint());  
        else printf("%d\n", array.find(x, y, i));
    }  
    return 0;  
}  

---

最后，就不带模板的粘一下可持久化数组的模板
由于struct内部有函数重载，有两个版本。

struct版本

struct Rope {
    static const int MAXSIZE = 2000005;
    int cnt, value[MAXSIZE << 4];
    int root[MAXSIZE << 4], lc[MAXSIZE << 4], rc[MAXSIZE << 4];
    void build(int &k, int l, int r) {  
        k = ++cnt;  
        if (l == r) {
            value[k] = a[l];
            return;
        }  
        int mid = (l + r) >> 1;  
        build(lc[k], l, mid);
        build(rc[k], mid + 1, r);  
    }  
    int query(int k, int l, int r, int pos) {  
        if (l == r) return value[k];  
        int mid = (l + r) >> 1;  
        if (pos <= mid) 
            return query(lc[k], l, mid, pos);  
        else return query(rc[k], mid + 1, r, pos);  
    }  
    void insert(int x, int &y, int l, int r, int pos, int val) {  
        y = ++cnt;  
        if (l == r) {
            value[y] = val;
            return;
        }  
        int mid = (l + r) >> 1;  
        lc[y] = lc[x]; rc[y] = rc[x];  
        if (pos <= mid) 
            insert(lc[x], lc[y], l, mid, pos, val);  
        else insert(rc[x], rc[y], mid + 1, r, pos, val);  
    }  
    void build(int l, int r) {
        build(root[0], l, r);
    }
    int find(int x, int y, int z) {  
        root[z] = root[x];
        return query(root[x], 1, n, y);   
    }  
    void insert(int x, int y, int pos, int val) {
        insert(root[x], root[y], 1, n, pos, val);
    }
};

class版本

class Rope {
    private:
        static const int MAXSIZE = 2000005;
        int cnt, value[MAXSIZE << 4];
        int root[MAXSIZE << 4], lc[MAXSIZE << 4], rc[MAXSIZE << 4];
        void build(int &k, int l, int r) {  
            k = ++cnt;  
            if (l == r) {
                value[k] = a[l];
                return;
            }  
            int mid = (l + r) >> 1;  
            build(lc[k], l, mid);
            build(rc[k], mid + 1, r);  
        }  
        int query(int k, int l, int r, int pos) {  
            if (l == r) return value[k];  
            int mid = (l + r) >> 1;  
            if (pos <= mid) 
                return query(lc[k], l, mid, pos);  
            else return query(rc[k], mid + 1, r, pos);  
        }  
        void insert(int x, int &y, int l, int r, int pos, int val) {  
            y = ++cnt;  
            if (l == r) {
                value[y] = val;
                return;
            }  
            int mid = (l + r) >> 1;  
            lc[y] = lc[x]; rc[y] = rc[x];  
            if (pos <= mid) 
                insert(lc[x], lc[y], l, mid, pos, val);  
            else insert(rc[x], rc[y], mid + 1, r, pos, val);  
        }  
    public:
        void build(int l, int r) {
            build(root[0], l, r);
        }
        int find(int x, int y, int z) {  
            root[z] = root[x];
            return query(root[x], 1, n, y);   
        }  
        void insert(int x, int y, int pos, int val) {
            insert(root[x], root[y], 1, n, pos, val);
        }
};