2019年春季个人训练赛第九场（老生场）
巧遇几道做过的题，然后就写的很舒服
链接
问题 A: 错排
题目描述
求有多少种长度为n的序列A，满足以下条件：
1.1~n这n个数在序列中各出现了一次。
2.若第i个数Ai的值为i，则称i是稳定的。序列恰好有m个数是稳定的。
满足条件的序列可能很多，序列数对1e9+7取模。输入
第一行一个数T，表示有T组数据。
接下来T行，每行两个整数n,m。输出
输出T行，每行一个数，表示求出的序列数
样例输入
5 1 0 1 1 5 2 100 50 10000 5000样例输出
0 1 20 578028887 60695423提示
T=500000,n,m≤1e6
数据有梯度。
错排公式 d[n] = (n-1)*(d[n-1]+d[n-2])
容易得出，答案为C（n,m）*d[n-m]，但是，d[0]并没有什么意义，但是对于这里的乘法来说确实必须写成d[0] = 1的
#include
using namespace std;
typedef long long ll;
const int maxn = 1e6+7,mod = 1e9+7;
ll d[maxn] = {1,0,1};//d[1] = 0,d[2] = 1
ll f[maxn] = {1},inv[maxn];
ll Pow(ll a,ll b,ll ans = 1){
for(a%=mod;b;b>>=1,a=a*a%mod)if(b&1)ans=ans*a%mod;
return ans;
}
void init(){
for(int i=3;i<=1e6;i++)d[i] = (d[i-1]+d[i-2])%mod*(i-1)%mod;//mistake
for(int i=1;i<=1e6;i++)f[i] = f[i-1]*i%mod;//n!
inv[(int)1e6] = Pow(f[(int)1e6],mod-2);
for(int i=1e6-1;~i;i--)inv[i]=inv[i+1]*(i+1)%mod;//inv n!
}
ll C(int n,int m){
return inv[n-m]*inv[m]%mod*f[n]%mod;
}
int main(){
init();
int t,n,m;
scanf("%d",&t);
while(t--){
scanf("%d%d",&n,&m);
printf("%lld\n",C(n,m)*d[n-m]%mod);
}
return 0;
}
问题 D: 余数求和
之前做过了
问题 F: 超级GCD
给两个数A，B。求gcd(A,B)
0≤A,B≤1e10000
java基操，注意递归的写法会炸内存，所以写成了迭代，其实大数自带gcd函数
即
System.out.println(a.gcd(b));自己写的慢一点，内存大一点
BigInteger a,b,c;
a = cin.nextBigInteger();
b = cin.nextBigInteger();
if(a.compareTo(b)<0){
c = a;
a = b;
b = c;
}
while(b != BigInteger.ZERO) {
c = b;
b = a.mod(b);
a = c;
}
System.out.println(a);
问题 J: Find Symmetries
题目描述
Snuke has two boards, each divided into a grid with N rows and N columns. For both of these boards, the square at the i-th row from the top and the j-th column from the left is called Square (i,j).
There is a lowercase English letter written in each square on the first board. The letter written in Square (i,j) is Si,j. On the second board, nothing is written yet.
Snuke will write letters on the second board, as follows:
First, choose two integers A and B ( 0≤A,BWrite one letter in each square on the second board. Specifically, write the letter written in Square (i+A,j+B) on the first board into Square (i,j) on the second board. Here, the k-th row is also represented as the (N+k)-th row, and the k-th column is also represented as the (N+k)-th column.
After this operation, the second board is called a good board when, for every i and j ( 1≤i,j≤N ), the letter in Square (i,j) and the letter in Square (j,i) are equal.
Find the number of the ways to choose integers A and B ( 0≤A,BConstraints
1≤N≤300
Si,j ( 1≤i,j≤N ) is a lowercase English letter.输入
Input is given from Standard Input in the following format:
N
S1,1S1,2..S1,N
S2,1S2,2..S2,N
:
SN,1SN,2..SN,N输出
Print the number of the ways to choose integers A and B ( 0≤A,B
样例输入
复制样例数据
2 ab ca样例输出
2提示
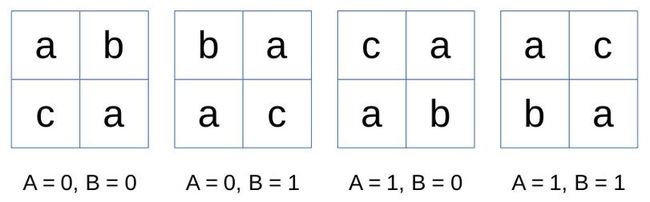
For each pair of A and B, the second board will look as shown below:
***
The second board is a good board when (A,B)=(0,1) or (A,B)=(1,0), thus the answer is 2.
给你一个二维数组，让你求有对
满足将原数组平移
暴力枚举的话O(n^4)
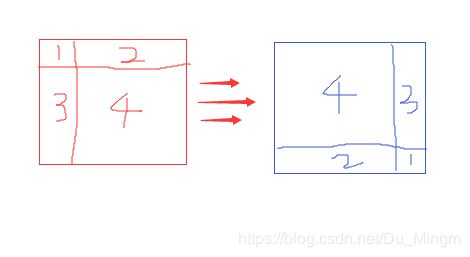
但是我们发现，如果一个图是good的话，((x+k)%n,(y+k)%n)之后还是对称的
嗯，差不多就是这样
由此我们可以由暴力
那么枚举k = y-x即可（易知k的范围为0到n-1），易知y-x等于0的时候相当于没动，
当某个k满足条件的时候，对答案的贡献是n（
于是代码
#include
using namespace std;
typedef unsigned long long ll;
const int maxn = 1e5+7,mod = 1e9+7;
char s[333][333],t[333][333];
int n,ans;
inline bool jude(int k){
for(int i=0;i 但是这样多一个数组，既浪费空间又浪费时间
所以可以，注意对应好下标的关系，
#include
using namespace std;
typedef unsigned long long ll;
const int maxn = 1e5+7,mod = 1e9+7;
char s[333][333];
int n,ans;
inline bool jude(int k){
for(int i=0;i
问题 K: 连锁店
题目描述
小D开了个饮料连锁店，连锁店共有n家，出售的饮料种类相同。为了促销，小D决定让每家连锁店开展赠送活动。具体来说，在第i家店，顾客可以用ai个饮料瓶兑换到bi瓶饮料和1个纪念币（注意不足ai个饮料瓶则不能兑换）。
一家店可以兑换多次，兑换得到的饮料瓶还可以继续用于兑换。
小C买了s瓶饮料，他想知道用这s瓶饮料最多可以兑换到多少个纪念币。输入
输入第一行为两个整数n,s，分别表示连锁店的数量和小C的饮料瓶数。
接下来n行，每行两个整数ai,bi，描述第i家饮料店的赠送活动。输出
输出一行一个整数，表示小C最多能兑换到的纪念币数量。若小C能兑换到无限多个纪念币，则输出−1。
样例输入
3 11 4 1 5 2 8 4样例输出
3提示
最多兑换到3个纪念币。兑换过程如下：
1.在第1家店用4瓶换1瓶，此时剩11−4+1=8瓶，有1个纪念币；
2.在第1家店用4瓶换1瓶，此时剩8−4+1=5瓶，有2个纪念币；
3.在第2家店用5瓶换2瓶，此时剩5−5+2=2瓶，有3个纪念币；
剩余的饮料瓶无法在任何店兑换，因此最多兑换到3个纪念币。
对于100%的数据，0≤n≤100000，0≤s≤1e19，0≤ai≤1e19，0≤bi≤1e19。
贪心
这题坑点蛮多的
首先是unsigned long long(1e19超范围了)
然后是贪心的方式，即按差值而非比值，（第二关键字是ai没问题）
再然后是答案的计算方式，要是不小心写成s/差值，就死了（例如5兑换4，答案是1而非5）
#include
using namespace std;
typedef unsigned long long ll;
const int maxn = 1e5+7,mod = 1e9+7;
struct node{ll x,y,z;}a[maxn];
bool operator < (const node a,const node b){
if(a.z != b.z)return a.z < b.z;
return a.xs)n--,i--;//一个优化，有没有都行
else if(a[i].x<=a[i].y)flag = 1;
a[i].z = a[i].x-a[i].y;
}
if(flag)return 0*puts("-1");
sort(a,a+n);
for(int i=0;i=a[i].x){
ll tmp = (s-a[i].x)/a[i].z+1;
ans += tmp;
s -= tmp*a[i].z;
}
}
printf("%llu\n",ans);
return 0;
}
问题 L: Zero-Sum Ranges
题目描述
We have an integer sequence A, whose length is N.
Find the number of the non-empty contiguous subsequences of A whose sums are 0. Note that we are counting the ways to take out subsequences. That is, even if the contents of some two subsequences are the same, they are counted individually if they are taken from different positions.
Constraints
1≤N≤2e5
−1e9≤Ai≤1e9
All values in input are integers.输入
Input is given from Standard Input in the following format:
N
A1 A2 … AN输出
Find the number of the non-empty contiguous subsequences of A whose sum is 0.
样例输入
6 1 3 -4 2 2 -2样例输出
3提示
There are three contiguous subsequences whose sums are 0: (1,3,−4), (−4,2,2) and (2,−2).
给你一个序列，让你求有多少个连续的区间使得区间和为0
暴力区间是O(N^3)，不可取，简化下，用前缀和优化一下是O(N^2)
观察式子
![\sum_{i=l}^{r}{a[i]} = sum[r]-sum[l-1]=0](http://img.e-com-net.com/image/info8/26758d57da01475f9d9cdbd1657b36ea.gif)
移项
![sum[r] = sum[l-1]](http://img.e-com-net.com/image/info8/c61ba234847a432ca37fa0c104f1418d.gif){kind=small}
统计下前缀和中某个数出现的次数
显然对于出现k次的这个数对答案的贡献是k*(k-1)/2，即C(k，2)
注意，对于sum[i] = 0要特判，因为它自己就可以对答案有贡献，即C(k,2)+C(k，1)
那么代码
#include
using namespace std;
typedef long long ll;
const int maxn = 2e5+7;
ll a[maxn],n,ans;
int main() {
map vis;
scanf("%lld",&n);
for(int i=1;i<=n;i++)
scanf("%lld",&a[i]),a[i] += a[i-1],vis[a[i]]++;
for(auto i:vis)
ans += i.second*(i.second-1)/2;
if(vis.count(0ll))ans += vis[0];
printf("%lld\n",ans);
return 0;
}