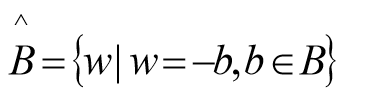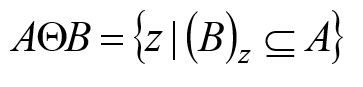数字图像处理第九章——形态学图像处理

数字图像处理—形态学图像处理

同样的，暂时对书上已经写得很清楚的知识点不再重复赘述，主要做一些总结，思考以及知识点的梳理和扩展。

（一）预备知识

介绍一下形态学中的一些基本概念。

1. 用数学形态学（也称图像代数）表示以形态为基础对图像进行分析的数学工具
2. 基本思想是用具有一定形态的结构元素去度量和提取图像中的对应形状以达到对图像分析识别的目的
3. 形态学图像处理的数学基础和所用语言是集合论
4. 形态学图像处理的应用可以简化图像数据， 保持它们基本的形状特性，并除去不相干的结 构
5. 形态学图像处理的基本运算有4个：膨胀、 腐蚀、开操作和闭操作

1.1 集合理论中的基本概念

介绍一下比较陌生的几个概念，其他的看书就好：

1. 所有像素坐标的集合均不属于集合A，记为$A^c$，由下式给出:
   
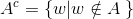
   这个集合称为集合A的补集。

2. 集合B的反射，定义为：
   
   即关于原集合原点对称 .

3. 集合A平移到点z=(z1,z2),表示为(A)z，定义为:
   

1.2 二值图像、集合及逻辑算子

二值图像：

二值图像(Binary Image)，按名字来理解只有两个值，0和1，0代表黑，1代表白，或者说0表示背景，而1表示前景。其保存也相对简单，每个像素只需要1Bit就可以完整存储信息。如果把每个像素看成随机变量，一共有N个像素，那么二值图有2的N次方种变化，而8位灰度图有255的N次方种变化，8为三通道RGB图像有255255255的N次方种变化。也就是说同样尺寸的图像，二值图像保存的信息更少。二值图像（binary image），即图像上的每一个像素只有两种可能的取值或灰度等级状态，人们经常用黑白、B&W、单色图像表示二值图像。

二值图像集合：

如果A和B是二值图像，那么C=A∪B仍是二值图像。这里，如 果 A 和B中相应的像素不是前景像素就是背景像素，那么 C中的这个像素就是前景像素。以第一种观点，函数 C由下式给出:

另一方面，运用集合的观点，C由下式给出：

集合运算：

1. A为图像集合，B为结构元素（集合）。
2. 数学形态学运算时B对A进行操作。
3. 结构元素要有1个原点（即结构元素参与形态学运算的参考点），可以是中心像素，原则上可选任何像素。
   注意：原点可以包含在结构元素中，也可以不包含在结构元素中，但运算的结果常不相同。

编码：

f = imread('D:\数字图像处理\第九章学习\Fig0903(a).tif');
g = imread('D:\数字图像处理\第九章学习\Fig0903(b).tif');
subplot(2,3,1), imshow(f);title('(a)二值图像 A:');
subplot(2,3,2), imshow(g);title('(b)二值图像 B:');
subplot(2,3,3), imshow(~f);title('(c)A的补集~A:');
subplot(2,3,4), imshow(f|g);title('(d) A和B的并集 A|B:');
subplot(2,3,5), imshow(f&g);title('(e)A和B的交集 A & B:');
subplot(2,3,6), imshow(f&~g);title('(f)A和B的差集 A&~B');

代码运行效果如下：

分析：

图像(d)是 “ UTK”和 “ GT” 图像的并集，包括来自两幅图像的所有前景像素。相反，两幅图像的交集(图(e))显示了字母 “ UTK”和 “ GT”中重叠的像素。最后，集合的差集图像(图(f))显示了 “ UTK”中除去 “ GT” 像素后的字母。

（二）膨胀和腐蚀

2.1 膨胀

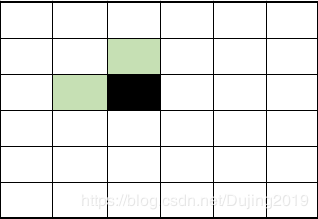
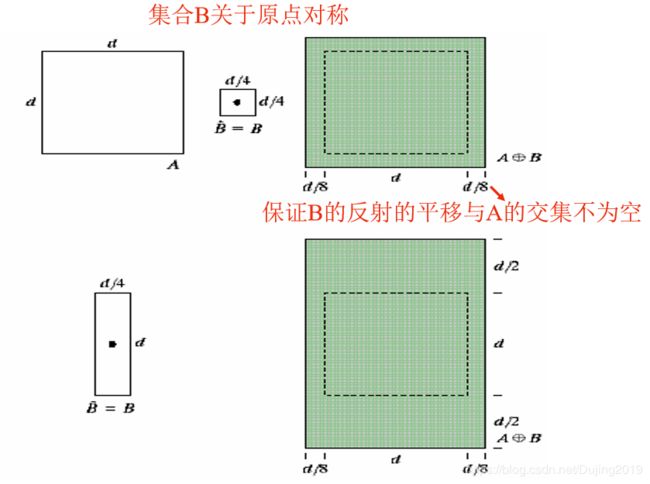
膨胀：膨胀是在二值图像中“加长”或“变粗”的操作。这种特殊的方式和变粗的程度由一个称为结构元素的集合控制。（实际就是将结构元素的原点与二值图像中的1重叠，将二值图像中重叠部分不是1的值变为1，完成膨胀）。

公式：

A和B是两个集合，A被B膨胀定义为：

公式解释：

1. B的反射进行平移与A的交集不为空。
2. B的反射：相对于自身原点的映象。
3. B的平移：对B的反射进行位移

图解：

      

(a)集合A    (b)结构元素B (黑色为原点所在)

      

(c)结构元素B的映像    (d)图中两种阴影部分（深色为扩大的部分）合起来为A+B

注意：

1. 膨胀运算只要求结构元素的原点在目标图像的内部平移，换句话说，当结构元素在目标图像上平移时，允许结构元素中的非原点像素超出目标图像的范围。
2. 膨胀运算具有扩大图像和填充图像中比结果元素小的成分的作用，因此在实际应用中可以利用膨胀运算连接相邻物体和填充图像中的小孔和狭窄的缝隙。

膨胀举例：

膨胀函数：

D = imdilate(A,B)

图像膨胀的应用：桥接文字裂缝

编码：

A = imread('D:\数字图像处理\第九章学习\Fig0906(a).tif');
B = [0 1 0; 1 1 1; 0 1 0];   %指定结构元素由0和1组成的矩阵
A2 = imdilate(A, B);    %二值图像
subplot(1,2,1), imshow(A);title('(a)包括断开文本的输入图像:');
subplot(1,2,2), imshow(A2);title('(b)膨胀后图像:');

图片中字体的加粗,且填充了字母中的小孔和狭窄的缝隙。

2.2 结构元的分解

公式：

公式理解：

B膨胀A等同于B1先膨胀A，再用B2膨胀之前的结果。

举例：

下面是由1组成的5x5数组的膨胀：

这个结构元能够分解为值为 1 的 5 元素行矩阵和值为 1 的 5 元素列矩阵:

分析：

在原结构元中，元素个数为 25; 但在行列分解后，总元素数目仅为 10。这意味着首先用 行结构元膨胀，再用列结构元膨胀，能够比 5x5 的数组膨胀快 2.5 倍。在实践中，速度的增长稍微慢一些，因为在每个膨胀运算中总有些其他开销。然而，由分解执行获得的速度方面的增 长仍然有很大意义。

2.3 strel函数

工具箱函数 strel 用于构造各种形状和大小的结构元。

基本语法：

se = strel(shape, parameters)

shape用于指定希望形状的字符串，parameters是描述形状信息的参数列表。

具体例子参考课本，是基础语法。

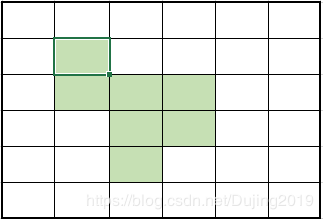
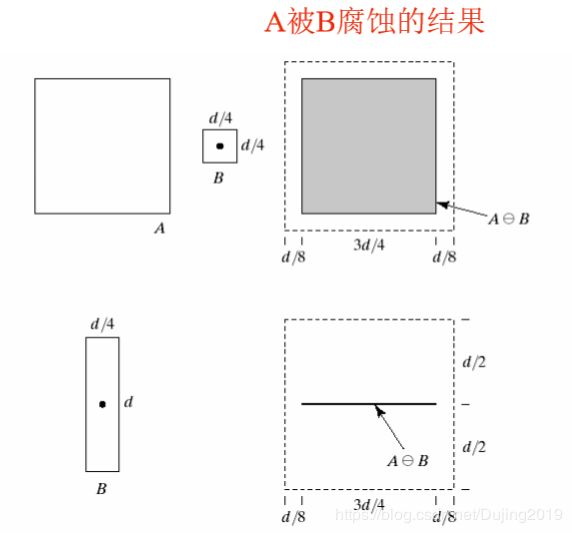
2.4 腐蚀

腐蚀：与膨胀相反，对二值图像中的对象进行“收缩”或“细化”。（实际上将结构元素的原点覆盖在每一个二值图像的1上，只要二值图像上有0和结构元素的1重叠，那么与原点重叠的值为0）同样由集合与结构元素完成。

公式：

A和B是两个集合，A被B腐蚀定义为：

公式解释：

1. A被 B 腐蚀是包含在A中的B由z平移的所有点z的集合。
2. B包含在A中的声明相当于B不共享A背景的任何元素。

图解：
     

(a)集合A(阴影部分)   (b)结构元素B（阴影部分，深色部分为原点）(c)阴影部分合起来为A-B

注意：

1. 当结构元素中原点位置不为1（也即原点不属于结构元素时），也要把它看作是1，也就是说，当在目标图像中找与结构元素B相同的子图像时，也要求子图像中与结构元素B的原点对应的那个位置的像素的值是1。
2. 腐蚀运算要求结构元素必须完全包括在被腐蚀图像内部：换句话说，当结构元素在目标图像上平移时，结构元素中的任何元素不能超过目标图像范围。
3. 腐蚀运算的结果不仅与结构元素的形状选取有关，而且还与原点位置的选取有关。
4. 腐蚀运算具有缩小图像和消除图像中比结构元素小的成分的作用，因此在实际应用中，可以利用腐蚀运算去除物体之间的粘连，消除图像中的小颗粒噪声。

腐蚀举例：

腐蚀函数：

A2 = imerode(A, se)

图像腐蚀应用：消除图像细节部分

编码：

f = imread('D:\数字图像处理\第九章学习\Fig0908(a).tif');
se = strel('disk', 10);
g = imerode(f, se);
se = strel('disk', 5);
g1 = imerode(f, se);
g2 = imerode(f, strel('disk', 20));
subplot(2,2,1), imshow(f);title('(a)原始图像的尺寸为480x480像素:');
subplot(2,2,2), imshow(g);title('(b)用半径为10的圆形腐蚀:');
subplot(2,2,3), imshow(g1);title('(c)用半径为5的圆形腐蚀:');
subplot(2,2,4), imshow(g2);title('(d)用半径为20的圆形腐蚀');

分析：

假设要除去图a中的细线，但想保留其他结构,可以选取足够小的结构元来匹配中心方块，但较粗的边缘线因太大而无法匹配全部线。图b几乎成功去掉了模板中的细线，图c中一些引线还没有去掉，图d中引线都被去掉了，但是边缘引线也丢失了，所以选取合适的结构元很重要。

（三） 膨胀与腐蚀的结合

3.1 开操作和闭操作

开操作：

1. 使图像的轮廓变得光滑，断开狭窄的间断和消除细的突出物。
2. 使用结构元素B对集合A进行开操作，定义为：
   
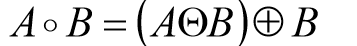
   先用B对A腐蚀，然后用B对结果膨胀。
3. 与开操作等价的数学表达式为:
   
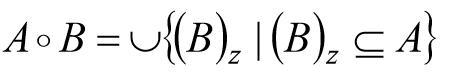
4. A o B 的边界通过B中的点完成。
5. B在A的边界内转动时，B中的点所能到达的A的边界的最远点。
   
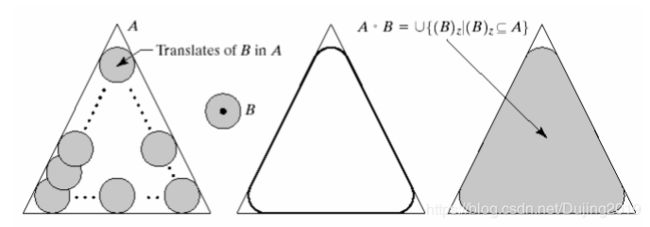
6. A o B 是 A的子集合。
7. 如果C是D的子集，则 C o B是 D o B的子集。
8. (A o B) o B = A o B

闭操作：

1. 同样使图像的轮廓变得光滑，但与开操作相反，它能消除狭窄的间断和长细的鸿沟，消除小的孔洞，并填补轮廓线中的裂痕。
2. 使用结构元素B对集合A进行闭操作，定 义为：
   
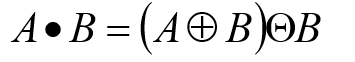
   先用B对A膨胀，然后用B对结果腐蚀。
3. A . B的边界通过B中的点完成 。
4. B在A的边界外部转动 :
   
5. A 是 A . B的子集合。
6. 如果C 是 D 的子集 ， 则C . B 是 D . B的子集。
7. (A . B) . B = A . B

工具箱函数：

开操作：

C = imopen(A, B)

闭操作:

C = imclose(A, B)

A为二值图像，B为0，1矩阵组成，并且是指定结构元素。

函数imopen 和 imclose 的应用：

编码：

f = imread('D:\数字图像处理\第九章学习\Fig0910(a).tif');
se = strel('square', 40);
fo = imopen(f, se);
fc = imclose(f, se);
foc = imclose(fo, se);
subplot(2,2,1), imshow(f), title('(a)原图');
subplot(2,2,2), imshow(fo), title('(b)开操作');
subplot(2,2,3), imshow(fc), title('(c)闭操作');
subplot(2,2,4), imshow(foc), title('(d) (b)的闭操作结果');

分析：

1. 图(a)中的图像设计了一些用于演示开操作和闭操作的特征，比如细小突起、细的桥接点、几个弯口、孤立的小洞、 小的孤立物和齿状边缘。
2. 图 (b)显示了结果。注意，从图中可以看出，细的突出和外部点的边缘的不规则部分被去除掉了，细的桥接和小的孤立物也被去除了。
3. 图 ©中的结果: 这里，细的弯口、内部的不规则边缘和小洞都被去除了。先做开操作的闭操作的结果有平滑效果.
4. 图 (d)显示了平滑过的物体。

噪声滤波器：

先开操作再闭操作，构成噪声滤波器。

编码：

f = imread('D:\数字图像处理\第九章学习\Fig0911(a).tif');
se = strel('square', 6);
fo = imopen(f, se);
foc = imclose(fo, se);
subplot(1,3,1), imshow(f), title('(a)带噪声的指纹图像');
subplot(1,3,2), imshow(fo), title('(b)图像的开操作');
subplot(1,3,3), imshow(foc), title('(c)先用开操作，再用闭操作');

分析：

1. 图(a)是受噪声污染的指纹二值图像，噪声为黑色背景上的亮元素和亮指纹部分的暗元素。
2. 图(b)所示的图像。发现，对图像进行开操作可以去除噪声点，但是这种处理在指纹的纹脊上又引入一些缺口。
3. 图( c )显示了最终结果。在这个结果中，大多数噪声被消除了，开运算的闭运算可以给指纹填充缺口，但是指纹纹路并没有完全恢复 。

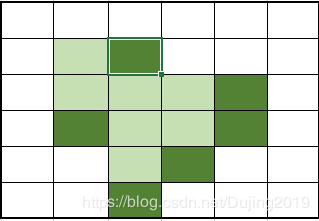
3.2 击中或击不中变换

击中击不中变换（HMT），HMT变换可以同时探测图像的内部和外部。研究解决目标图像识别和模式识别等领域，在处理目标图像和背景的关系上能够取得更好的效果。

作用：形状检测的基本工具。

公式：

A中对B进行的匹配（击中）表示为：

B1是由与一个对象相联系的B元素构成的集合，B1是由与一个对象相联系的B元素构成的集合。

图解：

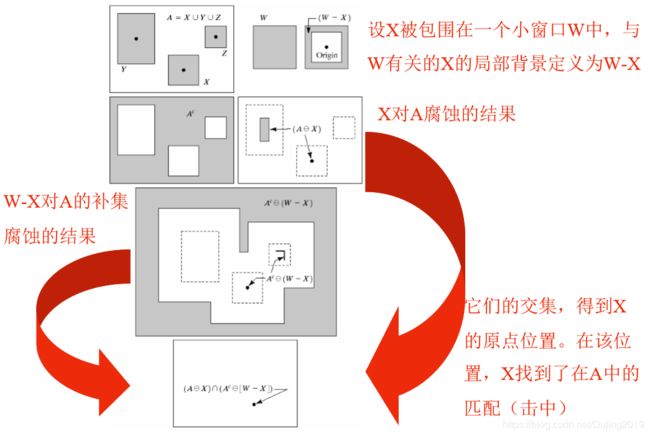
工具箱函数：

C = bwhitmiss(A, B1, B2)

其中的 C为结果，A为输入图像，B1、B2表示结构元素。

定位图像中物体左上角的像素：

编码：

f = imread('D:\数字图像处理\第九章学习\Fig0913(a).tif');
B1 = strel([0 0 0;0 1 1; 0 1 0]);
B2 = strel([1 1 1;1 0 0;1 0 0]);
g = bwhitmiss(f,B1,B2);
subplot(1,2,1), imshow(f), title('(a)原始图像');
subplot(1,2,2), imshow(g), title('(b)击中、击不中变换的结果');

分析：

1. 图(a)显示了包括各种尺寸的正方形图像。我们要定位有东、南相邻像素(这些 “击中”）和没有东北、北、西北、西和西南相邻像素(这些 “击不中”）的前景像素。这些要求导致以下B1,B2两个结构元。这两个结构元都不包括东南邻域像素，这称为不关心像素。用函数 bwhitmiss 来计算变换。
2. 图 (b)中的每个单像素点都是图 (a)中物体左上角的像素。图 (b)中是放大后的像素，以便更清晰。bwhitmiss的替代语法可以把Bl 和 B2 组合成间隔矩阵。只要 B1等于 1 或-1，B2 等于 1, 间隔矩阵就等于 1。对于不关心像素，间隔矩阵等于 0。

3.3 bwmorph函数

工具箱函数 bwmorph 执行许多以膨胀、腐蚀和查找表运算相结合为基础的形态学操作， 调用语法为：

g = bwmorph(f, operation, n);

f 是输入的二值图像，operation 是指定所希望运算的字符串，n 是指定重复次数的正整数。

细化：

f = imread('D:\数字图像处理\第九章学习\Fig0911(a).tif');
g1 = bwmorph(f, 'thin',1);
g2 = bwmorph(f, 'thin',2);
ginf = bwmorph(f,'thin', Inf);
subplot(1,4,1),imshow(f);title('(a)指纹图像:');
subplot(1,4,2),imshow(g1);title('(b)细化一次后的指纹图像:');
subplot(1,4,3),imshow(g2);title('(c)细化两次后的图像:');
subplot(1,4,4),imshow(ginf);title('(d)一直细化到稳定状态的图像：');

骨骼化：

f = imread('D:\数字图像处理\第九章学习\Fig0916(a).tif');
fs = bwmorph(f,'skel',Inf);
for k = 1:5
    fa = fs & ~endpoints(fs);
end
subplot(1,3,1),imshow(f);title('(a)骨头图像:');
subplot(1,3,2),imshow(fs);title('(b)使用函数 bwmorph 得到的骨豁:');
subplot(1,3,3),imshow(fa);title('（c)使用函数 endpoint 裁剪后的骨豁：');

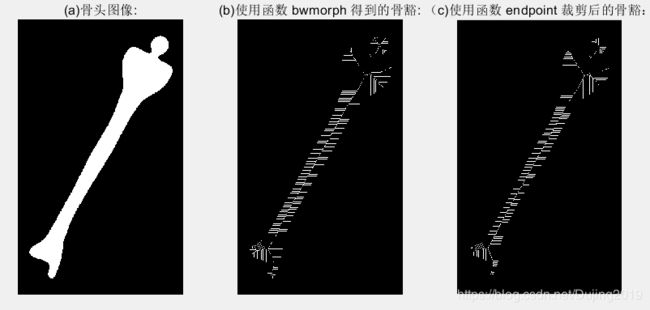
分析：骨骼化(Gonzalez和 Woods[2008])是另一种减少二值图像中的物体为一组细“笔画”的方法, 这些细骨豁仍保留原始物体形状的重要信息。当 operation 置为 'skel '时，函数 bwmorph 执行骨骼化。令 f 代表图(a)中类似骨头的图像，为了计算骨骼，调用 bwmorph, 令 n=Inf，图(b)显示了骨骼化的结果，与物体的基本形状相似。骨骼化和细化经常产生短的无关的“毛刺” ，有时这被叫做寄生成分。清除(或除去)这些“毛刺”的处理称为裁剪。方法是反复确认并去除端点。通过 5 次去除端点的迭代，得以后处理骨骼化图像 fs，图(c )显示了结果。

（四）标记连通分量

工具箱函数：

[L, num] = bwlabel (f, conn)

f 是输入二值图像，coon指定希望的连接方式（不是4连接就是8连接），输出L叫做标记矩阵，函数num则给出找到的连通分量总数。

计算和显示连通分量的质心:

f = imread('D:\数字图像处理\第九章学习\Fig0917(a).tif');
imshow(f);title('(a)标注连通分量原始图像:');
[L,n]=bwlabel(f);        %L为标记矩阵，n为找到连接分量的总数
[r,c]=find(L==3);        %返回第3个对象所有像素的行索引和列索引 
rbar=mean(r);
cbar=mean(c);
figure,imshow(f);title('(b)标记所有对象质心后的图像:');
hold on            %保持当前图像使其不被刷新
for k=1:n
   [r,c]=find(L==k);
   rbar=mean(r);
   cbar=mean(c);
   plot(cbar,rbar,'Marker','o','MarkerEdgeColor','k',...
        'MarkerFaceColor','k','MarkerSize',10);
   plot(cbar,rbar,'Marker','*','MarkerFaceColor','w'); %其中的marker为标记
end

（五）形态学重建

概述：重构是一种涉及到两幅图像和一个结构元素的形态学变换。一幅图像，即标记，是变换的开始点。另一幅图像是掩膜，用来约束变换过程。结构元素用于定义连接性。

定义：若G是掩膜，f为标记，则从f重构g可以记为$R_g$(f)，由下列的迭代过程定义：

1. 将h1初始化为标记图像f。
2. 创建结构元素 ：B = ones(3)。
3. 重复
   
   直到
   
   其中，标记f必须是g的一个子集。

函数：

out = imreconstruct(marker,mask)

masker是标记，mask是掩膜。

5.1 通过重建进行开操作

在形态学开操作中，腐蚀典型地去除小的物体，且随后的膨胀趋向于恢复保留的物体形状。 然而，这种恢复的精确度取决于形状和结构元之间的相似性。本节讨论的方法，通过重建进行开操作能准确地恢复腐蚀之后的物体形状。用结构元B对图像 G通过重建进行开操作可定义为 :

f = imread('D:\数字图像处理\第九章学习\Fig0917(a).tif');
subplot(3,2,1),imshow(f);title('(a)重构原始图像');
fe=imerode(f,ones(51,1));%竖线腐蚀
subplot(3,2,2),imshow(fe);title('(b)使用竖线腐蚀后的结果');
fo=imopen(f,ones(51,1));%竖线做开运算
subplot(3,2,3),imshow(fo);title('(c)使用竖线做开运算结果');
fobr=imreconstruct(fe,f);%fe做标记
subplot(3,2,4),imshow(fobr);title('(d)使用竖线做重构开运算');
ff=imfill(f,'holes');%对f进行孔洞填充
subplot(3,2,5),imshow(ff);title('(e)对f填充孔洞后的图像');
fc=imclearborder(f,8);%清除边界，2维8邻接
subplot(3,2,6),imshow(fc);title('(f)对f清除边界后的图像');

分析：

1. 传统开运算中，腐蚀去除掉小对象，随后的膨胀恢复原始对象形状，但受元素结构影响，恢复的往往不是很精确。
2. 重构则能精确恢复原始图像。

5.2 填充孔洞

令I表示二值图像，假设我们选择标记图像F，除了图像边缘外，其余部分都为 0, 边缘部分设值为 1-I:

函数：

g = imfill(f,‘holes’);

5.3 清除边界物体

定义标记图像F为：

其中，/是原始图像，然后以/作为模板图像，重建

得到一幅图像H, 其中仅包含与边界接触的物体。

函数：

g = imclearborder(f,conn)

f 是输入图像，g 是结果。conn 的值不是 4 就是 8(默认)。 物体更亮且与图像边界相连接的结构。

（六）灰度级形态学

6.1 膨胀和腐蚀

灰度图像的形态学梯度定义为膨胀运算与腐蚀运算的结果之间的差值。

膨胀定义：

1. 使用结构元素b对f的灰度膨胀定义为：
   
   其中，$D_f$和$D_b$分别是f和b的定义域，f和b是函数而不是二值形态学情况中的集合。

2. 当结构元素b是平坦的，即b(x,y)在其定义域内都为0时：
   

腐蚀定义：

1. 使用结构元素b对f的灰度腐蚀定义为：
   
   其中，$D_f$和$D_b$分别是f和b的定义域。

2. 当结构元素b是平坦的，即b(x,y)在其定义域内都为0时：
   

膨胀和腐蚀操作：

编写代码：

f = imread('D:\数字图像处理\第九章学习\Fig0923(a).tif');
se=strel('square',3);  %构造了一个平坦的3x3的结构元素
gd=imdilate(f,se);    %对原图像进行膨胀操作
ge=imerode(f,se);     %对原图像进行腐蚀操作
morph_grad=imsubtract(gd,ge); %从膨胀的图像中减去腐蚀过得图像产生一个形态学梯度。
subplot(3,2,1);imshow(f,[]);title('(a)原始图像');
subplot(3,2,2),imshow(gd,[]);title('(b)膨胀的图像');
subplot(3,2,3),imshow(ge,[]);title('(c)腐蚀的图像');
subplot(3,2,4),imshow(morph_grad,[]);title('(d)形态学梯度');

分析 ：

1. 膨胀得到的图像比原图像更明亮，并且减弱或消除小的，暗的细节部分。即比原图像模糊。
2. 腐蚀得到的图像更暗，并且尺寸小，明亮的部分被削弱 。

6.2 开操作和闭操作

图像开运算：

1. 在灰度图像中，开操作的表达式与二值图像拥有相同的形式。
   
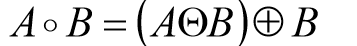
2. 把一幅图像看做是一个三维表明，其亮度值代表xy平面上的高度值，则当结构元素b在f下面活动时，结构元素的任何部分的最高值构成了开运算的结果。
3. 先进行腐蚀操作可以除去小的亮的图像细节，但这样会使图像变暗，接下来进行膨胀操作增强图像的整体亮度。

图像闭运算：

1. 在灰度图像中，闭操作的表达式与二值图像拥有相同的形式。
   
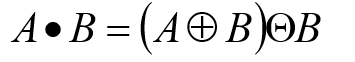
2. 当结构元素b在f的上面活动时，结构元素的任何部分的最低值构成了闭运算的结果 。
3. 先通过膨胀操作除去图像中的暗细节，同时增加图像的亮度，接下来对图像进行腐蚀，而不会将膨胀操作除去的部分重新引入图像中。

用开操作和闭操作做形态学平滑 ：

f = imread('D:\数字图像处理\第九章学习\Fig0925(a).tif');
subplot(3,2,1),imshow(f);  
title('(a)木钉图像原图');   
se=strel('disk',5);     %disk其实就是一个八边形  
fo=imopen(f,se);        %经过开运算  
subplot(3,2,2),imshow(f);  
title('(b)使用半径5的disk开运算后的图像');   
foc=imclose(fo,se);  
subplot(3,2,3),imshow(foc);  
title('(c)先开后闭的图像'); 
focd=imclose(f,se);  
subplot(3,2,4),imshow(focd);  
title('(d)原始图像的闭操作'); 
foce=imopen(focd,se);  
subplot(3,2,5),imshow(foce);  
title('(e)先闭后开的图像'); 
fasf=f;  
for i=2:5  
    se=strel('disk',i);  
    fasf=imclose(imopen(fasf,se),se);  
end  
subplot(3,2,6),imshow(fasf);  
title('(f)使用开闭交替滤波后图像'); 

分析：

1. 图 (b)显示了开操作的图像 fo, 在这里，我们看到，亮区域己经被调低了(平滑)，木钉上的暗条文几乎没有受影响。
2. 图 (c )显示了开操作的闭操作 foe。现在我们注意到，暗区域已经被平滑得很好了，结果是整个图像得到全部平滑。这种过程通常叫做开-闭滤波。先开运算后闭运算构成噪声滤波器，用来平滑图像并去除噪声。
3. 图 (d)显示了原始图像的闭操作结果。木钉上的暗条文已经被平滑掉了，主要留下了亮的细节(注意背景中的亮条文)。
4. 图 (e)显示了这些条文的平滑和木钉表面的进一步平滑效果。最终结果是原始图像得到全部平滑。
5. 图(f)是交替顺序滤波，交替顺序滤波的一种形式是用不断增大的一系列结构元执行开-闭滤波，刚开始用小的结构元，增加大小，直到与图 (b)和©中结构元的大小相同为止。交替顺序滤波与单个开-闭滤波相比，处理图像更平滑一些。

非均匀背景的补偿 ：

f = imread('D:\数字图像处理\第九章学习\Fig0926(a).tif');
g = f>=(255*graythresh(f));
se=strel('disk',100);
fo=imopen(f,se);
f2=imsubtract(f,fo); 
g1 = f2>=(255*graythresh(f2));
subplot(2,3,1),imshow(f);  
title('(a)原始图像');  
subplot(2,3,2),imshow(g);  
title('(b)经过阈值处理后的图像');   
subplot(2,3,3),imshow(f);  
title('(c)原图开运算后的图像');  
subplot(2,3,4),imshow(f2);  
title('(d)原图减去开运算');  
subplot(2,3,5),imshow(g1);  
title('(e)最终结果');  

分析：

1. 图 (a) :显示了一幅米粒的图像f，图像下部的背景比上部的黑。这样的话，对不平坦的亮度进行阈值处理会很困难。
2. 图 (b) "是阈值处理方案，图像顶端的米粒被很好地从背景中分离开来，但是图像底部的米粒没有从背景中正确地提取出来。
3. 图(c ):对图像进行开操作，可以产生对整个图像背景的合理估计。
4. 图(d) :把图(c )从原始图像中减去，生成一幅拥有合适的均勾背景的米粒图像.
5. 图(e):显示了新的经阈值处理后的图像。注意，改进效果超过了图 (b)。

粒度测定 :

颗粒分析：形态学技术可以用与间接地度量颗粒的大小分布，但不能准确地识别每一个颗粒。对于形状规则且亮于背景大的颗粒，基本方法是应用不断增大尺寸的形态学开运算。

f = imread('D:\数字图像处理\第九章学习\Fig0926(a).tif');
sumpixels=zeros(1,36);  
for k=0:35  
    se=strel('disk',k);  
    fo=imopen(f,se);  
    sumpixels(k+1)=sum(fo(:));  
end    
%可以看到，连续开运算之间的表面积会减少  
plot(0:35,sumpixels),xlabel('k'),ylabel('surface area');  
title('(a)表面积和结构元素半径之间的关系');  
figure,plot(-diff(sumpixels));%diff()函数为差分或者近似倒数，即相邻2个之间的差值  
xlabel('k'),ylabel('surface area reduction');  
title('(b)减少的表面积和结构元素半径之间的关系'); 

分析：

1. (a)连续开运算之间的表面积会减小。
2. (b)图峰值表明出现了大量的有着这种半径的对象。

6.3 重建

重建：

1. h极小值变换：标记图像是由掩膜挑选ing减去常量所得。
2. 开运算重建：先腐蚀后重建。
3. 闭运算重建：对图像求补、计算其开操作重建并对结果求补。

重建移去复杂的背景 ：

f = imread('D:\数字图像处理\第九章学习\Fig0930(a).tif');
subplot(3,3,1),imshow(f);  
title('(a)原图像');    
f_obr=imreconstruct(imerode(f,ones(1,71)),f);  
subplot(3,3,2),imshow(f_obr);  
title('(b)重建的开操作');   
f_o=imopen(f,ones(1,71));    
subplot(3,3,3),imshow(f_o);  
title('(c)开操作');    
f_thr=imsubtract(f,f_obr);    %顶帽重构
subplot(3,3,4),imshow(f_thr);  
title('(d)重建的顶帽操作');  
f_th=imsubtract(f,f_o)    %标准顶帽运算，方便比较
subplot(3,3,5),imshow(f_th);  
title('(e)顶帽操作');  
g_obr=imreconstruct(imerode(f_thr,ones(1,11)),f_thr);  
subplot(3,3,6),imshow(g_obr);  
title('(f)用水平线对(b)经开运算后重建图');   
g_obrd=imdilate(g_obr,ones(1,2));  
subplot(3,3,7),imshow(g_obrd);  
title('(g)使用水平线对(f)进行膨胀');  
f2=imreconstruct(min(g_obrd,f_thr),f_thr);  
subplot(3,3,8),imshow(f2);  
title('(h)最后的重建结果');  

分析：

为了消除每个键盘上方的水平反射光，利用这些反射比图像中任何文本字符都要宽的这个事实。用长水平线的结构元执行重建的开操作，重建的开操作(f_obr) 显示于图(b)中。为了进行对比，图(c )显示了标准的开操作 (f_o) 。重建的开操作在提取水平的相邻键之间的背景方面的确较好。从原始图像中减去重建的开操作被称为顶帽重建 , 结果示于图 (d)中。消除图 (d)中键右边的垂直反射光。这可以通过用短的水平线执行重建的开操作来完成，在这个结果中(见图 (f))，垂直的反射光不见了。但是，包括字母的垂直的细笔画也不见了。我们利用了那些已被错误消除的字母非常接近第一次膨胀(见图 (g))后还存在的其他字符这一事实，以 f_thr 作为模板，以 min(g_obrd,f_thr) 作为标记，图 (h)显示了最后的结果。注意，背景上键盘的阴影和反射光都成功去除了。