机器学习——神经网络
机器学习——神经网络
- (一)算法原理
- 1.1 深度学习要解决的问题
- 1.2 深度学习应用领域
- 1.3 计算机视觉任务
- 1.4 得分函数
- 1.5 损失函数
- 1.6 模型表示
- 1.7 样本和直观理解
- 1.8 多类分类
- 1.9 代价函数
- (二)代码实现
(一)算法原理
1.1 深度学习要解决的问题
机器学习流程:
- 数据获取
- 特征工程(最核心的一部分)
- 建立模型
- 评估与应用
特征工程的作用:
- 数据特征决定了模型的上限。
- 预处理和特征提取是最核心的。
- 算法与参数选择决定了如何逼近这个上限。
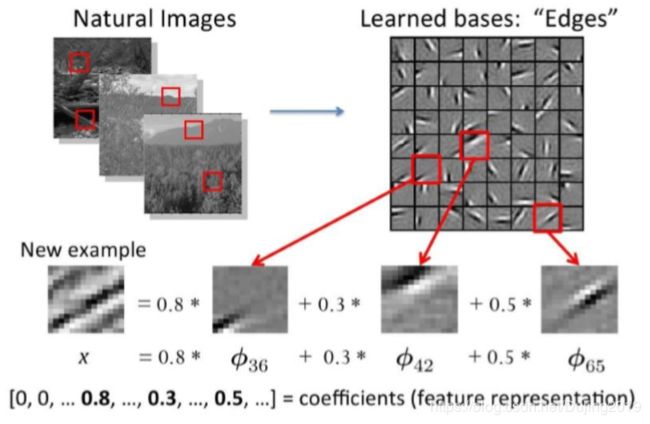
特征如何提取:
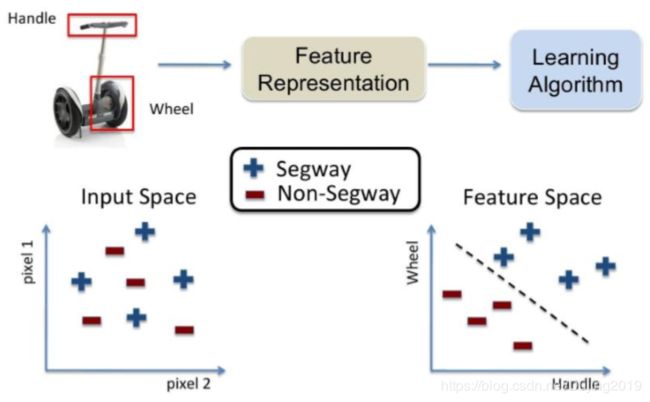
深度学习解决的核心问题是怎么样去提取特征,什么样的特征是最合适的。
1.2 深度学习应用领域
1.无人驾驶(检测和识别)
2.人脸识别
3.医学

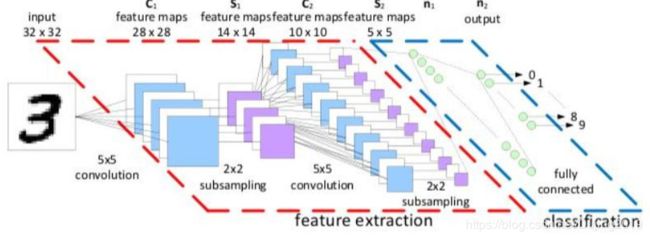
1.3 计算机视觉任务
图像表示:计算机眼中的图像

一张图片被表示成三维数组的形式,每个像素的值从0到255
例如:300x100x3
1.4 得分函数
从输入到输出的映射
f ( x , W ) = W x + b f(x,W)=Wx+b f(x,W)=Wx+b
算出每个类别的得分
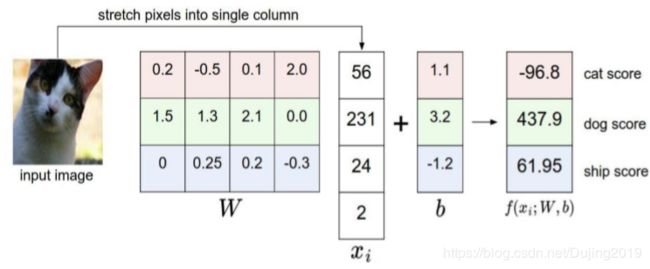
多重权重构成决策边界
f ( x i , W , b ) = W x i f(x_{i},W,b)=Wx_{i} f(xi,W,b)=Wxi+b
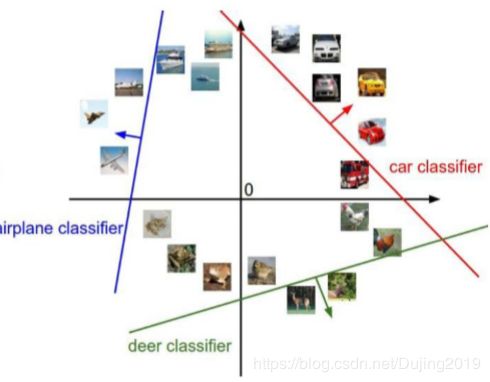
1.5 损失函数
L i = ∑ j ≠ y i m a x ( 0 , s j − s y i + 1 ) L_{i}=\sum_{j\neq y_{i}}^{}max(0,s_{j}-s_{yi}+1) Li=j̸=yi∑max(0,sj−syi+1)
L 1 = m a x ( 0 , 5.1 − 3.2 + 1 ) + m a x ( 0 , − 1.7 − 3.2 + 1 ) L_{1}=max(0,5.1-3.2+1)+max(0,-1.7-3.2+1) L1=max(0,5.1−3.2+1)+max(0,−1.7−3.2+1)
= m a x ( 0 , 2.9 ) + m a x ( 0 , − 13.9 ) =max(0,2.9)+max(0,-13.9) =max(0,2.9)+max(0,−13.9)
= 2.9 + 0 =2.9+0 =2.9+0
= 2.9 =2.9 =2.9
L 2 = m a x ( 0 , 5.1.3 − 4.9 + 1 ) + m a x ( 0 , − 2.0 − 4.9 + 1 ) L_{2}=max(0,5.1.3-4.9+1)+max(0,-2.0-4.9+1) L2=max(0,5.1.3−4.9+1)+max(0,−2.0−4.9+1)
= m a x ( 0 , − 2.6 ) + m a x ( 0 , − 1.9 ) =max(0,-2.6)+max(0,-1.9) =max(0,−2.6)+max(0,−1.9)
= 0 + 0 =0+0 =0+0
= 0 =0 =0
L 3 = m a x ( 0 , 2.2 − ( − 3.1 ) + 1 ) + m a x ( 0 , 2.5 − ( − 3.1 ) + 1 ) L_{3}=max(0,2.2-(-3.1)+1)+max(0,2.5-(-3.1)+1) L3=max(0,2.2−(−3.1)+1)+max(0,2.5−(−3.1)+1)
= m a x ( 0 , 5.3 ) + m a x ( 0 , 5.6 ) =max(0,5.3)+max(0,5.6) =max(0,5.3)+max(0,5.6)
= 5.3 + 5.6 =5.3+5.6 =5.3+5.6
= 10.9 =10.9 =10.9
如何损失函数的值相同,那么意味着两个模型一样吗?否定的
f ( x , W ) = W x f(x,W)=Wx f(x,W)=Wx
L = 1 N ∑ i = 1 N ∑ j ≠ y i m a x ( 0 , f ( x i ; W ) j − f ( x i ; W ) y j + 1 ) L=\frac{1}{N}\sum_{i=1}^{N}\sum_{j\neq y_{i}}^{}max(0,f(x_{i};W)_{j}-f(x_{i};W)_{yj}+1) L=N1∑i=1N∑j̸=yimax(0,f(xi;W)j−f(xi;W)yj+1)
输入数据: x = [ 1 , 1 , 1 , 1 ] x=[1,1,1,1] x=[1,1,1,1]
模型A: w 1 = [ 1 , 0 , 0 , 0 ] w_{1}=[1,0,0,0] w1=[1,0,0,0]
模型B: w 2 = [ 0.25 , 0.25 , 0.25 , 0.25 ] w_{2}=[0.25,0.25,0.25,0.25] w2=[0.25,0.25,0.25,0.25]
w 1 T x = w 2 T x = 1 w_{1}^{T}x=w_{2}^{T}x=1 w1Tx=w2Tx=1
损失函数=数据损失+正则化惩罚项
L = 1 N ∑ i = 1 N ∑ j ≠ y i m a x ( 0 , f ( x i ; W ) j − f ( x i ; W ) y j + 1 ) + λ R ( W ) L=\frac{1}{N}\sum_{i=1}^{N}\sum_{j\neq y_{i}}^{}max(0,f(x_{i};W)_{j}-f(x_{i};W)_{yj}+1)+\lambda R(W) L=N1∑i=1N∑j̸=yimax(0,f(xi;W)j−f(xi;W)yj+1)+λR(W)
正则化惩罚项: R ( W ) = ∑ k ∑ l W k , l 2 R(W)=\sum_{k}^{}\sum_{l}^{}W_{k,l}^{2} R(W)=∑k∑lWk,l2
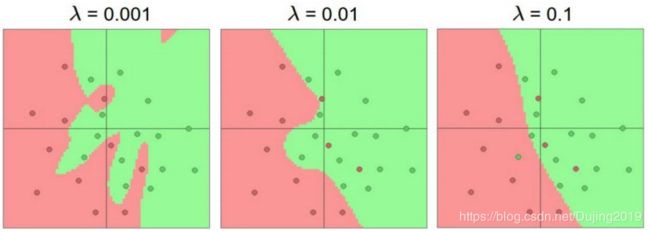
(模型不要太复杂,过拟合的模型是没有用的)
Softmax分类器
现在我们得到的是一个输入的得分值,但如果给我一个概率值会更好!如何把一个得分值转换成一个概率值呢?
g ( z ) = 1 1 + e − z g(z)=\frac{1}{1+e^{-z}} g(z)=1+e−z1
归一化:
P ( Y = k ∣ X = x i ) = e s k ∑ j e s j P(Y=k|X=x_{i})=\frac{e^{s}k}{\sum_{j}^{}e^{sj}} P(Y=k∣X=xi)=∑jesjesk where s = f ( x i ; W ) s=f(x_{i};W) s=f(xi;W)
计算损失值: L i = − l o g P ( Y = y i ∣ X = x i ) L_{i}=-logP(Y=y_{i}|X=x_{i}) Li=−logP(Y=yi∣X=xi)
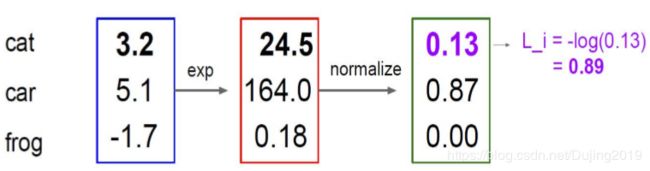
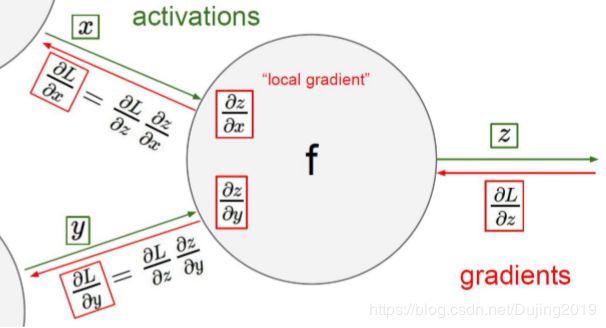
反向传播
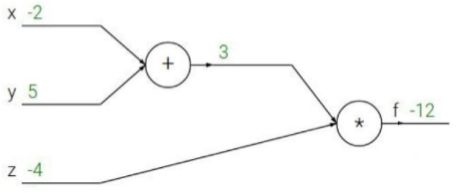
f ( x , y , z ) = ( x + y ) z f(x,y,z)=(x+y)z f(x,y,z)=(x+y)z
x = − 2 , y = 5 , z = − 4 x=-2,y=5,z=-4 x=−2,y=5,z=−4
q = x + y q=x+y q=x+y
∂ q ∂ x = 1 ∂ q ∂ y = 1 \frac{\partial q}{\partial x}=1 \frac{\partial q}{\partial y}=1 ∂x∂q=1∂y∂q=1
f = q z f=qz f=qz
∂ f ∂ q = z ∂ f ∂ z = q \frac{\partial f}{\partial q}=z \frac{\partial f}{\partial z}=q ∂q∂f=z∂z∂f=q
f ( w , x ) = 1 1 + e − ( w 0 x 0 + w 1 x 1 + w 2 ) f(w,x)=\frac{1}{1+e^{-(w_{0}x_{0}+w_{1}x_{1}+w_{2})}} f(w,x)=1+e−(w0x0+w1x1+w2)1
σ ( x ) = 1 1 + e − x \sigma (x)=\frac{1}{1+e^{-x}} σ(x)=1+e−x1
d σ ( x ) d x = e − x ( 1 + e − x ) 2 = ( 1 + e − x − 1 1 + e − x ) ( 1 + 1 + e − x ) = ( 1 − σ ( x ) ) σ ( x ) \frac{d\sigma (x)}{dx}=\frac{e^{-x}}{(1+e^{-x})^{2}}=\left ( \frac{1+e^{-x}-1}{1+e^{-x}}\right )\left ( \frac{1+}{1+e^{-x}}\right )=(1-\sigma (x))\sigma (x) dxdσ(x)=(1+e−x)2e−x=(1+e−x1+e−x−1)(1+e−x1+)=(1−σ(x))σ(x)
加法门单元:均等分配
MAX门单元:给最大的
乘法门单元:互换的感觉
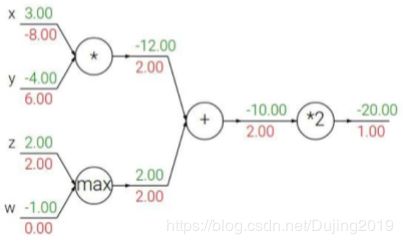
神经网络架构细节
线性方程: f = W x f=Wx f=Wx
非线性方程: f = W 2 m a x ( 0 , W 1 x ) f=W_{2}max(0,W_{1}x) f=W2max(0,W1x)
继续堆叠一层: f = W 3 m a x ( 0 , W 2 m a x ( 0 , W 1 x ) ) f=W_{3}max(0,W_{2}max(0,W_{1}x)) f=W3max(0,W2max(0,W1x))
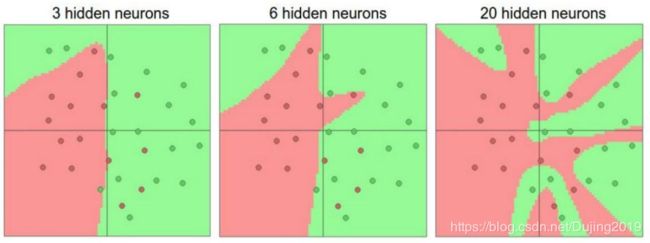
神经网络的强大之处在于,用更多的参数来拟合复杂的数据
1.6 模型表示
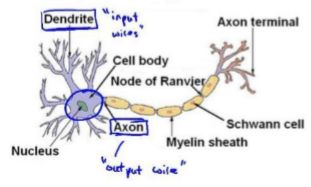
为了构建神经网络模型,我们需要首先思考大脑中的神经网络是怎样的?每一个神经元都可以被认为是一个处理单元/神经核(processing unit/Nucleus),它含有许多输入/树突(input/Dendrite),并且有一个输出/轴突(output/Axon)。神经网络是大量神经元相互链接并通过电脉冲来交流的一个网络。
神经网络模型建立在很多神经元之上,每一个神经元又是一个个学习模型。这些神经元(也叫激活单元,activation unit)采纳一些特征作为输出,并且根据本身的模型提供一个输出。下图是一个以逻辑回归模型作为自身学习模型的神经元示例,在神经网络中,参数又可被成为权重(weight)。
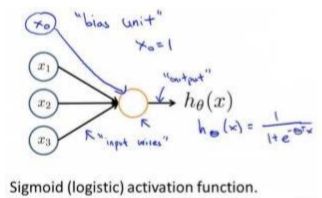
设计出了类似于神经元的神经网络,效果如下:
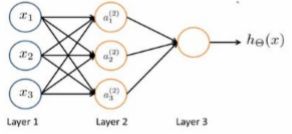
其中1, 2, 3是输入单元(input units),我们将原始数据输入给它们。 1, 2, 3是中间单元,它们负责将数据进行处理,然后呈递到下一层。 最后是输出单元,它负责计ℎ()。
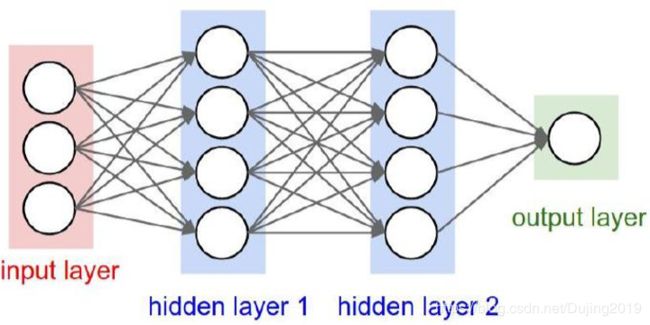
神经网络模型是许多逻辑单元按照不同层级组织起来的网络,每一层的输出变量都是下一层的输入变量。下图为一个 3 层的神经网络,第一层成为输入层(Input Layer),最后一层称为输出层(Output Layer),中间一层成为隐藏层(Hidden Layers)。我们为每一层都增加一个偏差单位(bias unit):
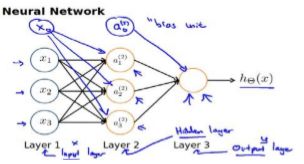
下面引入一些标记法来帮助描述模型:
a i ( j ) a_{i}^{(j)} ai(j) 代表第 层的第 个激活单元。 θ ( j ) \theta ^{(j)} θ(j) 代表从第 层映射到第 + 1 层时的权重的矩阵,例如 θ ( 1 ) \theta ^{(1)} θ(1)代表从第一层映射到第二层的权重的矩阵。其尺寸为:以第 + 1层的激活单元数量为行数,以第 层的激活单元数加一为列数的矩阵。例如:上图所示的神经网络中 θ ( 1 ) \theta ^{(1)} θ(1)的尺寸为 3*4。
对于上图所示的模型,激活单元和输出分别表达为:
a 1 ( 2 ) = g ( θ 10 ( 1 ) x 0 + θ 11 ( 1 ) x 1 + θ 12 ( 1 ) x 2 + θ 13 ( 1 ) x 3 ) a_{1}^{(2)}=g(\theta _{10}^{(1)}x_{0}+\theta _{11}^{(1)}x_{1}+\theta _{12}^{(1)}x_{2}+\theta _{13}^{(1)}x_{3}) a1(2)=g(θ10(1)x0+θ11(1)x1+θ12(1)x2+θ13(1)x3)
a 2 ( 2 ) = g ( θ 20 ( 1 ) x 0 + θ 21 ( 1 ) x 1 + θ 22 ( 1 ) x 2 + θ 23 ( 1 ) x 3 ) a_{2}^{(2)}=g(\theta _{20}^{(1)}x_{0}+\theta _{21}^{(1)}x_{1}+\theta _{22}^{(1)}x_{2}+\theta _{23}^{(1)}x_{3}) a2(2)=g(θ20(1)x0+θ21(1)x1+θ22(1)x2+θ23(1)x3)
a 3 ( 2 ) = g ( θ 30 ( 1 ) x 0 + θ 31 ( 1 ) x 1 + θ 32 ( 1 ) x 2 + θ 33 ( 1 ) x 3 ) a_{3}^{(2)}=g(\theta _{30}^{(1)}x_{0}+\theta _{31}^{(1)}x_{1}+\theta _{32}^{(1)}x_{2}+\theta _{33}^{(1)}x_{3}) a3(2)=g(θ30(1)x0+θ31(1)x1+θ32(1)x2+θ33(1)x3)
h θ ( x ) = g ( θ 10 ( 2 ) a 0 ( 2 ) + θ 11 ( 2 ) a 1 ( 2 ) + θ 12 ( 2 ) a 2 ( 2 ) + θ 12 ( 2 ) a 3 ( 2 ) ) h_{\theta}(x)=g(\theta _{10}^{(2)}a_{0}^{(2)}+\theta _{11}^{(2)}a_{1}^{(2)}+\theta _{12}^{(2)}a_{2}^{(2)}+\theta _{12}^{(2)}a_{3}^{(2)}) hθ(x)=g(θ10(2)a0(2)+θ11(2)a1(2)+θ12(2)a2(2)+θ12(2)a3(2))
上面进行的讨论中只是将特征矩阵中的一行(一个训练实例)给了神经网络,需要将整个训练集都给神经网络算法来学习模型。
可以知道:每一个都是由上一层所有的和每一个所对应的决定的。 (把这样从左到右的算法称为前向传播算法( FORWARD PROPAGATION ))
把, , 分别用矩阵表示,我们可以得到 ⋅ = :
X = x 0 x 1 x 2 x 3 , θ = θ 10 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . θ 33 , a = a 1 a 2 a 3 X=\begin{matrix} x_{0}\\ x_{1}\\ x_{2}\\ x_{3}\end{matrix},\theta =\begin{matrix} \theta _{10} & ... &... & ...\\ ... & ... & ... & ...\\ ...&... & ... & \theta _{33} \end{matrix},a=\begin{matrix} a_{1}\\ a_{2}\\ a_{3}\end{matrix} X=x0x1x2x3,θ=θ10..............................θ33,a=a1a2a3
( FORWARD PROPAGATION ) 相对与使用循环来编码,利用向量化的方法会使得计算更为简便。以上面的神经网络为例,试着计算第二层的值:
x = [ x 0 x 1 x 2 x 3 ] x=\begin{bmatrix} x_{0}\\ x_{1}\\ x_{2}\\ x_{3}\end{bmatrix} x=⎣⎢⎢⎡x0x1x2x3⎦⎥⎥⎤
z ( 2 ) = [ z 1 ( 2 ) z 2 ( 2 ) z 3 ( 2 ) ] z^{(2)}=\begin{bmatrix} z_{1}^{(2)}\\ z_{2}^{(2)}\\ z_{3}^{(2)}\\ \end{bmatrix} z(2)=⎣⎢⎡z1(2)z2(2)z3(2)⎦⎥⎤
z ( 2 ) = θ ( 1 ) x z^{(2)}=\theta ^{(1)}x z(2)=θ(1)x
a ( 2 ) = g ( z ( 2 ) ) a^{(2)}=g(z^{(2)}) a(2)=g(z(2))
g ( [ θ 10 ( 1 ) θ 11 ( 1 ) θ 12 ( 1 ) θ 13 ( 1 ) θ 20 ( 1 ) θ 21 ( 1 ) θ 22 ( 1 ) θ 23 ( 1 ) θ 30 ( 1 ) θ 31 ( 1 ) θ 32 ( 1 ) θ 33 ( 1 ) ] × [ x 0 x 1 x 2 x 3 ] ) g\left ( \begin{bmatrix} \theta _{10}^{(1)} & \theta _{11}^{(1)} & \theta _{12}^{(1)} &\theta _{13}^{(1)} \\ \theta _{20}^{(1)} & \theta _{21}^{(1)} & \theta _{22}^{(1)} &\theta _{23}^{(1)} \\ \theta _{30}^{(1)}& \theta _{31}^{(1)} & \theta _{32}^{(1)} & \theta _{33}^{(1)} \end{bmatrix}\times \begin{bmatrix} x_{0}\\ x_{1}\\ x_{2}\\ x_{3}\end{bmatrix}\right ) g⎝⎜⎜⎛⎣⎢⎡θ10(1)θ20(1)θ30(1)θ11(1)θ21(1)θ31(1)θ12(1)θ22(1)θ32(1)θ13(1)θ23(1)θ33(1)⎦⎥⎤×⎣⎢⎢⎡x0x1x2x3⎦⎥⎥⎤⎠⎟⎟⎞=
g ( [ θ 10 ( 1 ) x 0 + θ 11 ( 1 ) x 1 + θ 12 ( 1 ) x 2 + θ 13 ( 1 ) x 3 + θ 20 ( 1 ) x 0 + θ 21 ( 1 ) x 0 + θ 22 ( 1 ) x 2 + θ 23 ( 1 ) x 3 + θ 30 ( 1 ) x 0 + θ 31 ( 1 ) x 0 + θ 32 ( 1 ) x 0 + θ 33 ( 1 ) x 0 ] ) = [ a 1 ( 2 ) a 2 ( 2 ) a 3 ( 2 ) ] g\left ( \begin{bmatrix} \theta _{10}^{(1)}x_{0}+\theta _{11}^{(1)}x_{1}+\theta _{12}^{(1)}x_{2}+\theta _{13}^{(1)}x_{3}\\ +\theta _{20}^{(1)}x_{0}+\theta _{21}^{(1)}x_{0}+\theta _{22}^{(1)}x_{2}+\theta _{23}^{(1)}x_{3}\\ +\theta _{30}^{(1)}x_{0}+\theta _{31}^{(1)}x_{0}+\theta _{32}^{(1)}x_{0}+\theta _{33}^{(1)}x_{0}\end{bmatrix}\right )=\begin{bmatrix} a_{1}^{(2)}\\ a_{2}^{(2)}\\ a_{3}^{(2)}\end{bmatrix} g⎝⎜⎛⎣⎢⎡θ10(1)x0+θ11(1)x1+θ12(1)x2+θ13(1)x3+θ20(1)x0+θ21(1)x0+θ22(1)x2+θ23(1)x3+θ30(1)x0+θ31(1)x0+θ32(1)x0+θ33(1)x0⎦⎥⎤⎠⎟⎞=⎣⎢⎡a1(2)a2(2)a3(2)⎦⎥⎤
令 z ( 2 ) z^{(2)} z(2) = θ ( 1 ) x \theta ^{(1)}x θ(1)x,则 a ( 2 ) a^{(2)} a(2) = z ( 2 ) z^{(2)} z(2) ,计算后添加 a 0 ( 2 ) a_{0}^{(2)} a0(2) = 1。 计算输出的值为:
g ( [ θ 10 ( 2 ) θ 11 ( 2 ) θ 12 ( 2 ) θ 13 ( 2 ) ] × [ a 1 ( 2 ) a 2 ( 2 ) a 3 ( 2 ) ] ) = g ( a 10 ( 2 ) a 0 ( 2 ) + a 11 ( 2 ) a 1 ( 2 ) + a 12 ( 2 ) a 2 ( 2 ) + a 13 ( 2 ) a 3 ( 2 ) ) = h θ ( x ) g\left ( \begin{bmatrix} \theta _{10}^{(2)} &\theta_{11}^{(2)} &\theta_{12}^{(2)} & \theta_{13}^{(2)} \end{bmatrix}\times \begin{bmatrix} a_{1}^{(2)}\\ a_{2}^{(2)}\\ a_{3}^{(2)}\end{bmatrix}\right )=g\left ( a_{10}^{(2)}a_{0}^{(2)}+a_{11}^{(2)}a_{1}^{(2)}+a_{12}^{(2)}a_{2}^{(2)}+a_{13}^{(2)}a_{3}^{(2)}\right )=h_{\theta}(x) g⎝⎜⎛[θ10(2)θ11(2)θ12(2)θ13(2)]×⎣⎢⎡a1(2)a2(2)a3(2)⎦⎥⎤⎠⎟⎞=g(a10(2)a0(2)+a11(2)a1(2)+a12(2)a2(2)+a13(2)a3(2))=hθ(x)
令 z ( 3 ) = θ ( 2 ) a ( 2 ) z^{(3)}=\theta ^{(2)}a^{(2)} z(3)=θ(2)a(2),则 h θ ( x ) = a ( 3 ) = g ( z ( 3 ) ) h_{\theta}(x)=a^{(3)}=g(z^{(3)}) hθ(x)=a(3)=g(z(3))
这只是针对训练集中一个训练实例所进行的计算。如果要对整个训练集进行计算,需要将训练集特征矩阵进行转置,使得同一个实例的特征都在同一列里。即:
z ( 2 ) = θ ( 1 ) × X T z^{(2)}=\theta ^{(1)} \times X^{T} z(2)=θ(1)×XT
a ( 2 ) = g ( z ( 2 ) ) a^{(2)}=g(z^{(2)}) a(2)=g(z(2))
为了更好了解 Neuron Networks 的工作原理,先把左半部分遮住:
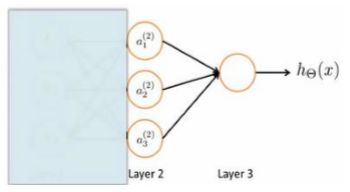
右半部分其实就是以 a 0 , a 1 , a 2 , a 3 a_{0},a_{1},a_{2},a_{3} a0,a1,a2,a3, 按照 Logistic Regression 的方式输出ℎ():
其实神经网络就像是 logistic regression,只不过我们把 logistic regression 中的输入向量 [ x 1 ∼ x 3 ] [x_{1}\sim x_{3}] [x1∼x3]变成了中间层的 [ a 1 ( 2 ) ∼ a 3 ( 2 ) ] [a_{1}^{(2)}\sim a_{3}^{(2)}] [a1(2)∼a3(2)],即:
g ( a 10 ( 2 ) a 0 ( 2 ) + a 11 ( 2 ) a 1 ( 2 ) + a 12 ( 2 ) a 2 ( 2 ) + a 13 ( 2 ) a 3 ( 2 ) ) = h θ ( x ) g\left ( a_{10}^{(2)}a_{0}^{(2)}+a_{11}^{(2)}a_{1}^{(2)}+a_{12}^{(2)}a_{2}^{(2)}+a_{13}^{(2)}a_{3}^{(2)}\right )=h_{\theta}(x) g(a10(2)a0(2)+a11(2)a1(2)+a12(2)a2(2)+a13(2)a3(2))=hθ(x)
可以把 a 0 , a 1 , a 2 , a 3 a_{0},a_{1},a_{2},a_{3} a0,a1,a2,a3看成更为高级的特征值,也就是 x 0 , x 1 , x 2 , x 3 x_{0},x_{1},x_{2},x_{3} x0,x1,x2,x3的进化体,并且它们是由 与决定的,因为是梯度下降的,所以是变化的,并且变得越来越厉害,所以这些更高级的特征值远比仅仅将 次方厉害,也能更好的预测新数据。
这就是神经网络相比于逻辑回归和线性回归的优势。
1.7 样本和直观理解
从本质上讲,神经网络能够通过学习得出其自身的一系列特征。在普通的逻辑回归中,被限制为使用数据中的原始特征 x 1 , x 2 , x 3 . . , x n , x_{1},x_{2},x_{3}..,x_{n}, x1,x2,x3..,xn,,虽然可以使用一些二项式项来组合这些特征,但是仍然受到这些原始特征的限制。在神经网络中,原始特征只是输入层,在上面三层的神经网络例子中,第三层也就是输出层做出的预测利用的是第二层的特征,而非输入层中的原始特征,可以认为第二层中的特征是神经网络通过学习后自己得出的一系列用于预测输出变量的新特征。
神经网络中,单层神经元(无中间层)的计算可用来表示逻辑运算,比如逻辑与(AND)、逻辑或(OR)。
举例说明:逻辑与(AND);下图中左半部分是神经网络的设计与 output 层表达式,右边上部分是 sigmod 函数,下半部分是真值表。
可以用这样的一个神经网络表示AND 函数:
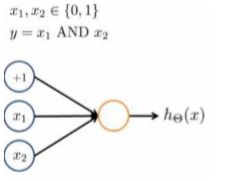
其中 θ 0 = − 30 \theta _{0}= −30 θ0=−30, θ 1 = 20 \theta _{1}= 20 θ1=20, θ 2 = 20 \theta _{2}= 20 θ2=20 ,输出函数 h θ ( x ) h_{\theta}(x) hθ(x)即为: h θ ( x ) = g ( − 30 + 20 x 1 + 20 x 2 ) h_{\theta}(x) = g(−30 + 20x_{1} +20x_{2}) hθ(x)=g(−30+20x1+20x2)
()的图像是:
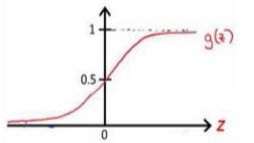

所以有: h θ ( x ) ≈ x 1 A N D x 2 h_{\theta}(x)\approx x_{1}ANDx_{2} hθ(x)≈x1ANDx2
OR 函数:

OR 与 AND 整体一样,区别只在于的取值不同。
二元逻辑运算符(BINARY LOGICAL OPERATORS)当输入特征为布尔值(0 或 1)时,我们可以用一个单一的激活层可以作为二元逻辑运算符,为了表示不同的运算符,我们之需要选择不同的权重即可。
下图的神经元(三个权重分别为-30,20,20)可以被视为作用同于逻辑与(AND):
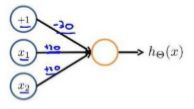
下图的神经元(三个权重分别为-10,20,20)可以被视为作用等同于逻辑或(OR):
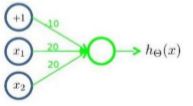
下图的神经元(两个权重分别为 10,-20)可以被视为作用等同于逻辑非(NOT):
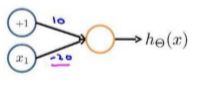
可以利用神经元来组合成更为复杂的神经网络以实现更复杂的运算。例如要实现 XNOR 功能(输入的两个值必须一样,均为 1 或均为 0),即:
X N O R = ( x 1 A N D x 2 ) O R ( ( N O T x 1 ) A N D ( N O T x 2 ) ) XNOR = (x_{1} AND x_{2}) OR((NOT x_{1})AND(NOT x_{2})) XNOR=(x1 AND x2) OR((NOT x1)AND(NOT x2))
首先构造一个能表达 ( N O T x 1 ) A N D ( N O T x 2 ) (NOT x_{1})AND(NOT x_{2}) (NOT x1)AND(NOT x2)部分的神经元:

然后将表示 AND 的神经元和表示 ( N O T x 1 ) A N D ( N O T x 2 ) (NOT x_{1})AND(NOT x_{2}) (NOT x1)AND(NOT x2)的神经元以及表示 OR 的神经元进行组合:
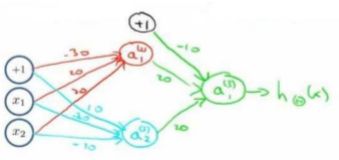
就得到了一个能实现 XNOR 运算符功能的神经网络。 按这种方法可以逐渐构造出越来越复杂的函数,也能得到更加厉害的特征值。 这就是神经网络的厉害之处。
1.8 多类分类
当有不止两种分类时(也就是 = 1,2,3….),比如以下这种情况,该怎么办?如果要训练一个神经网络算法来识别路人、汽车、摩托车和卡车,在输出层应该有 4 个值。例如,第一个值为 1 或 0 用于预测是否是行人,第二个值用于判断是否为汽车。
输入向量有三个维度,两个中间层,输出层 4 个神经元分别用来表示 4 类,也就是每一个数据在输出层都会出现 [ a b c d ] T \begin{bmatrix} a & b & c & d \end{bmatrix}^{T} [abcd]T,且,,,中仅有一个为 1,表示当前类。下面是该神经网络的可能结构示例:
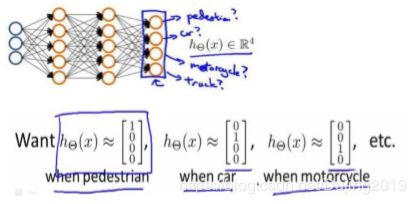
神经网络算法的输出结果为四种可能情形之一:

1.9 代价函数
假设神经网络的训练样本有个,每个包含一组输入和一组输出信号,表示神经网络层数,表示每层的 neuron 个数(表示输出层神经元个数),代表最后一层中处理单元的个数。
将神经网络的分类定义为两种情况:二类分类和多类分类,
二类分类: = 0, = 0 1表示哪一类;
类分类: = , = 1表示分到第 i 类;( > 2)
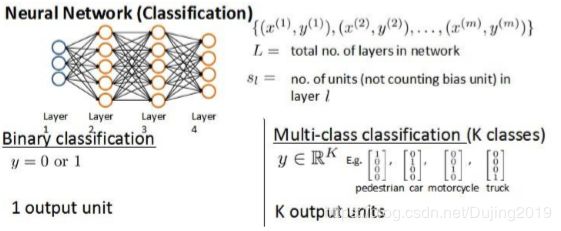
回顾逻辑回归问题中代价函数为:
J ( θ ) = − 1 m [ ∑ j = 1 n y ( i ) l o g h θ ( x ( i ) ) + ( 1 − y ( i ) ) l o g ( 1 − h θ ( x ( i ) ) ) ] + λ 2 m ∑ j = 1 n θ j 2 J(\theta)=-\frac{1}{m}\left [ \sum_{j=1}^{n}y^{(i)}logh_{\theta}(x^{(i)})+(1-y^{(i)})log(1-h_{\theta}(x^{(i)}))\right ]+\frac{\lambda }{2m}\sum_{j=1}^{n}\theta _{j}^{2} J(θ)=−m1[∑j=1ny(i)loghθ(x(i))+(1−y(i))log(1−hθ(x(i)))]+2mλ∑j=1nθj2
在逻辑回归中,只有一个输出变量,又称标量(scalar),也只有一个因变量,但是在神经网络中,可以有很多输出变量,ℎ()是一个维度为的向量,并且训练集中的因变量也是同样维度的一个向量,因此代价函数会比逻辑回归更加复杂一些,为:
J ( θ ) = − 1 m [ ∑ i = 1 m ∑ j = 1 n y k ( i ) ( l o g h θ ( x ( i ) ) ) k + ( 1 − y k ( i ) ) l o g ( 1 − ( h θ ( x ( i ) ) ) k ) ] + λ 2 m ∑ l = 1 L − 1 ∑ i = 1 s i ∑ j = 1 s i + 1 ( θ j i ( l ) ) 2 J(\theta)=-\frac{1}{m}\left [ \sum_{i=1}^{m}\sum_{j=1}^{n}y_{k}^{(i)}(logh_{\theta}(x^{(i)}))_{k}+(1-y_{k}^{(i)})log(1-(h_{\theta}(x^{(i)}))_{k})\right ]+\frac{\lambda }{2m}\sum_{l=1}^{L-1}\sum_{i=1}^{s_{i}}\sum_{j=1}^{s_{i}+1}(\theta _{ji}^{(l)})^{2} J(θ)=−m1[∑i=1m∑j=1nyk(i)(loghθ(x(i)))k+(1−yk(i))log(1−(hθ(x(i)))k)]+2mλ∑l=1L−1∑i=1si∑j=1si+1(θji(l))2
这个看起来复杂很多的代价函数背后的思想还是一样的,希望通过代价函数来观察算法预测的结果与真实情况的误差有多大,唯一不同的是,对于每一行特征,都会给出个预测,基本上可以利用循环,对每一行特征都预测个不同结果,然后在利用循环,在个预测中选择可能性最高的一个,将其与中的实际数据进行比较。
正则化的那一项只是排除了每一层 θ 0 \theta_{0} θ0后,每一层的 矩阵的和。最里层的循环循环所有的行(由 +1 层的激活单元数决定),循环则循环所有的列,由该层(层)的激活单元数所决定。即:ℎ()与真实值之间的距离为每个样本-每个类输出的加和,对参数进行regularization 的 bias 项处理所有参数的平方和。
之前在计算神经网络预测结果的时候采用了一种正向传播方法,从第一层开始正向一层一层进行计算,直到最后一层的ℎ()。
现在,为了计算代价函数的偏导数,需要采用一种反向传播算法,也就是首先计算最后一层的误差,然后再一层一层反向求出各层的误差,直到倒数第二层。 以一个例子来说明反向传播算法。 假设我们的训练集只有一个实例((1),(1)),我们的神经网络是一个四层的神经网络,其中 = 4 , = 4 , = 4:
前向传播算法:
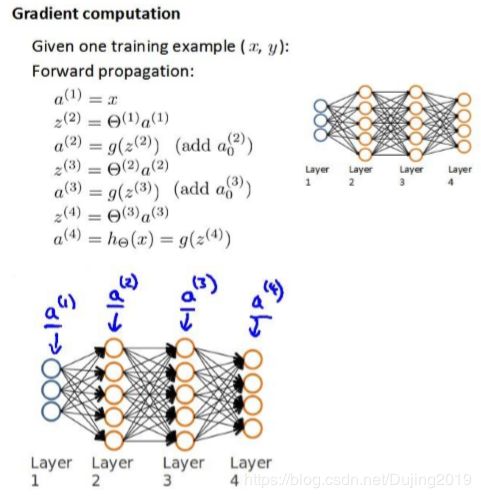
从最后一层的误差开始计算,误差是激活单元的预测 ( a k ( 4 ) ) (a_{k}^{(4)}) (ak(4))与实际值 ( y k ) (y^{k}) (yk) 之间的误差( = 1:)。用 δ \delta δ来表示误差,则: δ ( 4 ) = a ( 4 ) − y \delta^{(4)} =a^{(4)}-y δ(4)=a(4)−y
利用这个误差值来计算前一层的误差: δ ( 3 ) = ( θ ( 3 ) ) T δ ( 4 ) ∗ g ′ ( z ( 3 ) ) \delta^{(3)} =(\theta^{(3)})^{T}\delta ^{(4)}*{g}'(z^{(3)}) δ(3)=(θ(3))Tδ(4)∗g′(z(3))其中 g ′ ( z ( 3 ) ) {g}'(z^{(3)}) g′(z(3))是 形函数的导数, g ′ ( z ( 3 ) ) = a ( 3 ) ∗ ( 1 − a ( 3 ) ) {g}'(z^{(3)})=a^{(3)}*(1-a^{(3)}) g′(z(3))=a(3)∗(1−a(3))。而 ( θ ( 3 ) ) T δ ( 4 ) (\theta ^{(3)})^{T}\delta ^{(4)} (θ(3))Tδ(4)则是权重导致的误差的和。下一步是继续计算第二层的误差: δ ( 2 ) = ( θ ( 2 ) ) T δ ( 3 ) ∗ g ′ ( z ( 2 ) ) \delta ^{(2)}=(\theta^{(2)})^{T}\delta ^{(3)}*{g}'(z^{(2)}) δ(2)=(θ(2))Tδ(3)∗g′(z(2)) ,因为第一层是输入变量,不存在误差。有了所有的误差的表达式后,便可以计算代价函数的偏导数了,假设 = 0,即不做任何正则化处理时有: ∂ ∂ θ i j ( l ) J ( θ ) = a j ( l ) δ i l + 1 \frac{\partial}{\partial\theta _{ij}^{(l)}}J(\theta)=a_{j}^{(l)}\delta _{i}^{l+1} ∂θij(l)∂J(θ)=aj(l)δil+1
- 代表目前所计算的是第几层。
- 代表目前计算层中的激活单元的下标,也将是下一层的第个输入变量的下标。
- 代表下一层中误差单元的下标,是受到权重矩阵中第行影响的下一层中的误差单元
的下标。
如果考虑正则化处理,并且训练集是一个特征矩阵而非向量。在上面的特殊情况中,需要计算每一层的误差单元来计算代价函数的偏导数。在更为一般的情况中,同样需要计算每一层的误差单元,但是我们需要为整个训练集计算误差单元,此时的误差单元也是一个矩阵,用 Δ i j ( l ) \Delta _{ij}^{(l)} Δij(l)来表示这个误差矩阵。第 层的第 个激活单元受到第 个参数影响而导致的误差。
即首先用正向传播方法计算出每一层的激活单元,利用训练集的结果与神经网络预测的结果求出最后一层的误差,然后利用该误差运用反向传播法计算出直至第二层的所有误差。
在求出了 Δ i j ( l ) \Delta _{ij}^{(l)} Δij(l)之后,我们便可以计算代价函数的偏导数了,计算方法如下:
D i j ( l ) : = 1 m Δ i j l + λ θ i j ( l ) D_{ij}^{(l)}:=\frac{1}{m}\Delta _{ij}^{l}+\lambda \theta _{ij}^{(l)} Dij(l):=m1Δijl+λθij(l) i f j ≠ 0 if j\neq 0 ifj̸=0
D i j ( l ) : = 1 m Δ i j l D_{ij}^{(l)}:=\frac{1}{m}\Delta _{ij}^{l} Dij(l):=m1Δijl i f j = 0 if j= 0 ifj=0
随机初始化
任何优化算法都需要一些初始的参数。到目前为止都是初始所有参数为 0,这样的初始方法对于逻辑回归来说是可行的,但是对于神经网络来说是不可行的。如果令所有的初始参数都为 0,这将意味着我们第二层的所有激活单元都会有相同的值。同理,如果我们初始所有的参数都为一个非 0 的数,结果也是一样的。 通常初始参数为正负之间的随机值。
使用神经网络的注意事项:
- 网络结构:第一件要做的事是选择网络结构,即决定选择多少层以及决定每层分别有多
少个单元。 - 第一层的单元数即我们训练集的特征数量。
- 最后一层的单元数是我们训练集的结果的类的数量。
- 如果隐藏层数大于 1,确保每个隐藏层的单元个数相同,通常情况下隐藏层单元的个数
越多越好。 - 真正决定的是隐藏层的层数和每个中间层的单元数。
训练神经网络:
- 参数的随机初始化
- 利用正向传播方法计算所有的ℎ()
- 编写计算代价函数 的代码
- 利用反向传播方法计算所有偏导数
- 利用数值检验方法检验这些偏导数
- 使用优化算法来最小化代价函数
(二)代码实现
手写字体识别
import numpy as np
from utils.features import prepare_for_training
from utils.hypothesis import sigmoid, sigmoid_gradient
class MultilayerPerceptron:
#定义初始化函数
def __init__(self,data,labels,layers,normalize_data =False):
data_processed = prepare_for_training(data,normalize_data = normalize_data)[0]
self.data= data_processed
self.labels= labels
self.layers= layers #28x28x1=784 隐藏神经元个数25个 最终10分类任务
self.normalize_data= normalize_data
self.thetas = MultilayerPerceptron.thetas_init(layers)#初始化权重参数
def predict(self,data):
data_processed = prepare_for_training(data,normalize_data = self.normalize_data)[0]
num_examples = data_processed.shape[0]
predictions = MultilayerPerceptron.feedforward_propagation(data_processed,self.thetas,self.layers)
return np.argmax(predictions,axis=1).reshape((num_examples,1))
def train(self,max_iterations=1000,alpha=0.1):
unrolled_theta = MultilayerPerceptron.thetas_unroll(self.thetas)
(optimized_theta,cost_history) = MultilayerPerceptron.gradient_descent(self.data,self.labels,unrolled_theta,self.layers,max_iterations,alpha)
self.thetas = MultilayerPerceptron.thetas_roll(optimized_theta,self.layers)
return self.thetas,cost_history
@staticmethod
def thetas_init(layers):
num_layers = len(layers)
thetas = {}
for layer_index in range(num_layers - 1):
"""
会执行两次,得到两组参数矩阵:25*785 , 10*26
"""
in_count = layers[layer_index]
out_count = layers[layer_index+1]
# 这里需要考虑到偏置项,记住一点偏置的个数跟输出的结果是一致的
thetas[layer_index] = np.random.rand(out_count,in_count+1)*0.05 #随机进行初始化操作,值尽量小一点
return thetas
@staticmethod
def thetas_unroll(thetas):
num_theta_layers = len(thetas)
unrolled_theta = np.array([])
for theta_layer_index in range(num_theta_layers):
unrolled_theta = np.hstack((unrolled_theta,thetas[theta_layer_index].flatten()))
return unrolled_theta
@staticmethod
def gradient_descent(data,labels,unrolled_theta,layers,max_iterations,alpha):
optimized_theta = unrolled_theta
cost_history = []
for _ in range(max_iterations):
cost = MultilayerPerceptron.cost_function(data,labels,MultilayerPerceptron.thetas_roll(optimized_theta,layers),layers)
cost_history.append(cost)
theta_gradient = MultilayerPerceptron.gradient_step(data,labels,optimized_theta,layers)
optimized_theta = optimized_theta - alpha* theta_gradient
return optimized_theta,cost_history
@staticmethod
def gradient_step(data,labels,optimized_theta,layers):
theta = MultilayerPerceptron.thetas_roll(optimized_theta,layers)
thetas_rolled_gradients = MultilayerPerceptron.back_propagation(data,labels,theta,layers)
thetas_unrolled_gradients = MultilayerPerceptron.thetas_unroll(thetas_rolled_gradients)
return thetas_unrolled_gradients
@staticmethod
def back_propagation(data,labels,thetas,layers):
num_layers = len(layers)
(num_examples,num_features) = data.shape
num_label_types = layers[-1]
deltas = {}
#初始化操作
for layer_index in range(num_layers -1 ):
in_count = layers[layer_index]
out_count = layers[layer_index+1]
deltas[layer_index] = np.zeros((out_count,in_count+1)) #25*785 10*26
for example_index in range(num_examples):
layers_inputs = {}
layers_activations = {}
layers_activation = data[example_index,:].reshape((num_features,1))#785*1
layers_activations[0] = layers_activation
#逐层计算
for layer_index in range(num_layers - 1):
layer_theta = thetas[layer_index] #得到当前权重参数值 25*785 10*26
layer_input = np.dot(layer_theta,layers_activation) #第一次得到25*1 第二次10*1
layers_activation = np.vstack((np.array([[1]]),sigmoid(layer_input)))
layers_inputs[layer_index + 1] = layer_input #后一层计算结果
layers_activations[layer_index + 1] = layers_activation #后一层经过激活函数后的结果
output_layer_activation = layers_activation[1:,:]
delta = {}
#标签处理
bitwise_label = np.zeros((num_label_types,1))
bitwise_label[labels[example_index][0]] = 1
#计算输出层和真实值之间的差异
delta[num_layers - 1] = output_layer_activation - bitwise_label
#遍历循环 L L-1 L-2 ...2
for layer_index in range(num_layers - 2,0,-1):
layer_theta = thetas[layer_index]
next_delta = delta[layer_index+1]
layer_input = layers_inputs[layer_index]
layer_input = np.vstack((np.array((1)),layer_input))
#按照公式进行计算
delta[layer_index] = np.dot(layer_theta.T,next_delta)*sigmoid_gradient(layer_input)
#过滤掉偏置参数
delta[layer_index] = delta[layer_index][1:,:]
for layer_index in range(num_layers-1):
layer_delta = np.dot(delta[layer_index+1],layers_activations[layer_index].T)
deltas[layer_index] = deltas[layer_index] + layer_delta #第一次25*785 第二次10*26
for layer_index in range(num_layers -1):
deltas[layer_index] = deltas[layer_index] * (1/num_examples)
return deltas
@staticmethod
def cost_function(data,labels,thetas,layers):
num_layers = len(layers)
num_examples = data.shape[0]
num_labels = layers[-1]
#前向传播走一次
predictions = MultilayerPerceptron.feedforward_propagation(data,thetas,layers)
#制作标签,每一个样本的标签都得是one-hot
bitwise_labels = np.zeros((num_examples,num_labels))
for example_index in range(num_examples):
bitwise_labels[example_index][labels[example_index][0]] = 1
bit_set_cost = np.sum(np.log(predictions[bitwise_labels == 1]))
bit_not_set_cost = np.sum(np.log(1-predictions[bitwise_labels == 0]))
cost = (-1/num_examples) *(bit_set_cost+bit_not_set_cost)
return cost
@staticmethod
def feedforward_propagation(data,thetas,layers):
num_layers = len(layers)
num_examples = data.shape[0]
in_layer_activation = data
# 逐层计算
for layer_index in range(num_layers - 1):
theta = thetas[layer_index]
out_layer_activation = sigmoid(np.dot(in_layer_activation,theta.T))
# 正常计算完之后是num_examples*25,但是要考虑偏置项 变成num_examples*26
out_layer_activation = np.hstack((np.ones((num_examples,1)),out_layer_activation))
in_layer_activation = out_layer_activation
#返回输出层结果,结果中不要偏置项了
return in_layer_activation[:,1:]
@staticmethod
def thetas_roll(unrolled_thetas,layers):
num_layers = len(layers)
thetas = {}
unrolled_shift = 0
for layer_index in range(num_layers - 1):
in_count = layers[layer_index]
out_count = layers[layer_index+1]
thetas_width = in_count + 1
thetas_height = out_count
thetas_volume = thetas_width * thetas_height
start_index = unrolled_shift
end_index = unrolled_shift + thetas_volume
layer_theta_unrolled = unrolled_thetas[start_index:end_index]
thetas[layer_index] = layer_theta_unrolled.reshape((thetas_height,thetas_width))
unrolled_shift = unrolled_shift+thetas_volume
return thetas
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import matplotlib.image as mping
import math
from multilayer_perceptron import MultilayerPerceptron
data = pd.read_csv('../data/mnist-demo.csv')
numbers_to_display = 25
num_cells = math.ceil(math.sqrt(numbers_to_display))
plt.figure(figsize=(10,10))
for plot_index in range(numbers_to_display):
digit = data[plot_index:plot_index+1].values
digit_label = digit[0][0] #第一个位置
digit_pixels = digit[0][1:]#后面所有位置
image_size = int(math.sqrt(digit_pixels.shape[0]))
frame = digit_pixels.reshape((image_size,image_size))
plt.subplot(num_cells,num_cells,plot_index+1)
plt.imshow(frame,cmap='Greys')
plt.title(digit_label)
plt.subplots_adjust(wspace=0.5,hspace=0.5)
plt.show()
#构建训练模块
train_data = data.sample(frac = 0.8)
test_data = data.drop(train_data.index)
train_data = train_data.values
test_data = test_data.values
num_training_examples = 5000
x_train = train_data[:num_training_examples,1:]
y_train = train_data[:num_training_examples,[0]]
x_test = test_data[:,1:]
y_test = test_data[:,[0]]
layers=[784,25,10]
normalize_data = True
max_iterations = 500
alpha = 0.1
multilayer_perceptron = MultilayerPerceptron(x_train,y_train,layers,normalize_data)
(thetas,costs) = multilayer_perceptron.train(max_iterations,alpha)
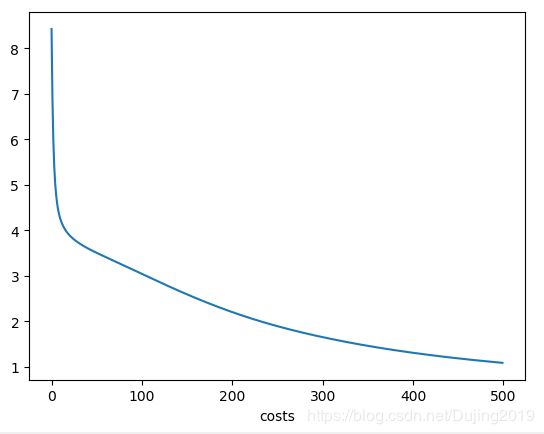
plt.plot(range(len(costs)),costs)
plt.xlabel('Grident steps')
plt.xlabel('costs')
plt.show()
y_train_predictions = multilayer_perceptron.predict(x_train)
y_test_predictions = multilayer_perceptron.predict(x_test)
train_p = np.sum(y_train_predictions == y_train)/y_train.shape[0] * 100
test_p = np.sum(y_test_predictions == y_test)/y_test.shape[0] * 100
print ('训练集准确率:',train_p)
print ('测试集准确率:',test_p)
numbers_to_display = 64
num_cells = math.ceil(math.sqrt(numbers_to_display))
plt.figure(figsize=(15, 15))
for plot_index in range(numbers_to_display):
digit_label = y_test[plot_index, 0]
digit_pixels = x_test[plot_index, :]
predicted_label = y_test_predictions[plot_index][0]
image_size = int(math.sqrt(digit_pixels.shape[0]))
frame = digit_pixels.reshape((image_size, image_size))
color_map = 'Greens' if predicted_label == digit_label else 'Reds'
plt.subplot(num_cells, num_cells, plot_index + 1)
plt.imshow(frame, cmap=color_map)
plt.title(predicted_label)
plt.tick_params(axis='both', which='both', bottom=False, left=False, labelbottom=False, labelleft=False)
plt.subplots_adjust(hspace=0.5, wspace=0.5)
plt.show()