Ceres的Options详解
目录
- 1、Ceres简介
- 2、常用通用参数
- 3、与优化算法相关的参数
- 3.1、优化方法无关参数
- 3.2、TRUST_REGION
- 3.3、LINE_SEARCH
- 4、与线性求解器有关的参数
1、Ceres简介
Ceres是一个非常优秀的非线性优化库(谷歌出品)。能完成很复杂的优化功能,选项也非常的多,本篇博客就来梳理下这些选项。Ceres的参数主要有三类,一类通用参数,比如迭代次数什么的;第二类是和优化算法的参数;第三类是和线性求解器(在信任域算法中被使用)有关的参数。
我在调Ceres Solver的优化的参数时,我首先会调最大迭代次数,然后换优化算法,调优化算法的参数,最后再调线性求解器的参数。
并不是所有的参数我都列出来了,我只列出常用的参数。
参考:solver-options。
2、常用通用参数
-
bool Solver::Options::IsValid(string *error) const
检查options是否合法,不合法的话返回false,并将错误信息存到error里面。 -
int Solver::Options::max_num_iterations
默认值:50
最大迭代次数。 -
double Solver::Options::max_solver_time_in_seconds
默认值:1e6
最长运行时间,单位为秒。 -
int Solver::Options::num_threads
默认值:1
Ceres用于评估Jacobian的线程数,越多优化速度越快。 -
DenseLinearAlgebraLibrary Solver::Options::dense_linear_algebra_library_type
默认值:EIGEN
Ceres支持使用多个密集线性代数库进行稠密矩阵分解。 目前可选的为EIGEN和LAPACK。 EIGEN始终可用;LAPACK指的是BLAS + LAPACK库,可能有也可能没有(得看编译Ceres库时有没有加入BLAS + LAPACK的支持)。
此设置会影响DENSE_QR,DENSE_NORMAL_CHOLESKY和DENSE_SCHUR求解器。 对于小到中等大小的求解器(这里的大小应该是指运算量,也就是问题规模的大小),EIGEN是一个很好的选择,但对于大问题,LAPACK + BLAS实现可以在性能上优势很大。 -
SparseLinearAlgebraLibrary Solver::Options::sparse_linear_algebra_library_type
默认值:SUITE_SPARSE > CX_SPARSE > EIGEN_SPARSE > NO_SPARSE
Ceres支持使用三个稀疏线性代数库SuiteSparse、CXSparse、EIGEN_SPARSE ,NO_SPARSE意味着不应使用稀疏线性求解器。
SuiteSparse是一个非常复杂的稀疏线性代数库(就是一群非常牛*的人写的),性能最好,推荐使用。如果SuiteSparse不可用(编译Ceres的时候没有加入SuiteSparse支持),请考虑使用CXSparse,这是一个更小,更容易编译的库。但是,它在大问题上的性能与SuiteSparse的性能相差巨大。也可以使用Eigen中稀疏线性代数库。目前,这个库的表现是三个中最差的。说不定在不久的将来性能会有改善。 -
int Solver::Options::num_linear_solver_threads
默认值:-1
这是一个废弃的选项,将在1.15中删除。 -
LoggingType Solver::Options::logging_type
默认值:PER_MINIMIZER_ITERATION
每次迭代都打印信息,另一个可选的为SILENT。 -
bool Solver::Options::minimizer_progress_to_stdout
默认值:false
默认情况下,Minimizer(优化器)进度会记录到stderr,具体取决于vlog级别。 如果此标志设置为true,并且Solver::Option:: logging_type不是SILENT,则日志记录输出将发送到stdout(在终端打印出信息)。
对于TRUST_REGION_MINIMIZER,进度显示如下:
iter cost cost_change |gradient| |step| tr_ratio tr_radius ls_iter iter_time total_time
0 4.185660e+06 0.00e+00 1.09e+08 0.00e+00 0.00e+00 1.00e+04 0 7.59e-02 3.37e-01
1 1.062590e+05 4.08e+06 8.99e+06 5.36e+02 9.82e-01 3.00e+04 1 1.65e-01 5.03e-01
2 4.992817e+04 5.63e+04 8.32e+06 3.19e+02 6.52e-01 3.09e+04 1 1.45e-01 6.48e-01
1. cost 是目标函数的值。
2. cost_change 是目标函数值的变化。
3. |gradient| 是梯度的最大范数。
4. |step| 是参数向量的变化。
5. tr_ratio是目标函数值的实际变化与信赖域模型值的变化之比。
6. tr_radius是信任区域半径的大小。
7. ls_iter是用于计算信任区域步骤的线性求解器迭代次数。
8. total_time是所用的总时间。
对于LINE_SEARCH_MINIMIZER,进度显示如下:
0: f: 2.317806e+05 d: 0.00e+00 g: 3.19e-01 h: 0.00e+00 s: 0.00e+00 e: 0 it: 2.98e-02 tt: 8.50e-02
1: f: 2.312019e+05 d: 5.79e+02 g: 3.18e-01 h: 2.41e+01 s: 1.00e+00 e: 1 it: 4.54e-02 tt: 1.31e-01
2: f: 2.300462e+05 d: 1.16e+03 g: 3.17e-01 h: 4.90e+01 s: 2.54e-03 e: 1 it: 4.96e-02 tt: 1.81e-01
1. f是目标函数的值。
2. d是目标函数的值的变化。
3. g是梯度的最大范数。
4. h是参数向量的变化。
5. s是线搜索计算的最佳步长。
6. it是当前迭代所花费的时间。
7. tt是最小化器所用的总时间。
-
bool Solver::Options::check_gradients
默认值:false
检查由具有有限差分的每个残差块计算的所有雅可比行列式,比较结果,如果它们大不相同,则优化失败。如果设置为true的花比较耗费性能,一般保持默认。 -
double Solver::Options::gradient_check_relative_precision
默认值: 1e8
在gradient checker中检查的精度。 如果雅可比行列式中的元素之间的相对差异超过此数字,则dump该cost term的雅可比行列式。 -
vector Solver::Options::callbacks
在Minimizer的每次迭代结束时执行的回调。 它们按照在此vector中指定的顺序执行。 默认情况下,参数仅在优化结束时更新。 如果希望在执行回调时访问更新的参数,则将Solver::Options::update_state_every_iteration需要设置为true。 -
bool Solver::Options::update_state_every_iteration
默认值:false
如果为true,则在每个迭代结束时更新参数,否则在优化终止时才更新参数。更多细节请参考链接。
3、与优化算法相关的参数
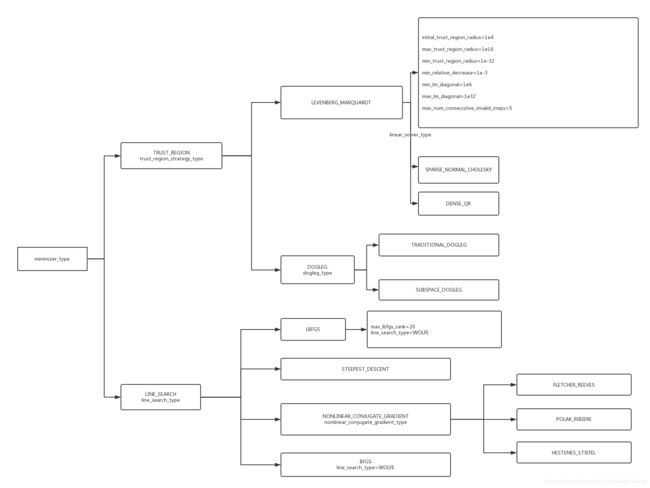
在Ceres中,求解优化问题有两类方法:信任域(TRUST_REGION)和线性搜索(LINE_SEARCH,尚不支持边界约束),和它们相关的主要的参数如下图所示(小写的是选项):
3.1、优化方法无关参数
-
MinimizerType Solver::Options::minimizer_type
默认值:TRUST_REGION
可选的为LINE_SEARCH和TRUST_REGION,这是非线性优化的两类算法。参考:Trust Region Methods 、 Line Search Methods。 -
double Solver::Options::gradient_tolerance
默认值:1e-10
求解器会在满足
∥ x − Π ⊞ ( x , − g ( x ) ) ∥ ∞ < = gradient_tolerance \|x - \Pi \boxplus(x, -g(x))\|_\infty <= \text{gradient\_tolerance} ∥x−Π⊞(x,−g(x))∥∞<=gradient_tolerance
时停止求解。其中||⋅||∞是指最大范数,Π是对边界约束的投影,⊞是与参数矢量相关的整体局部参数化的加法运算。
3.2、TRUST_REGION
-
double Solver::Options::function_tolerance
默认值:1e-6
求解器会在满足:
∣ Δ cost ∣ cost < = function_tolerance \frac{|\Delta \text{cost}|}{\text{cost}} <= \text{function\_tolerance} cost∣Δcost∣<=function_tolerance
时停止求解,其中Δcost是Levenberg-Marquardt方法中当前迭代中目标函数值(也就是损失函数)的变化。上面的公式可以这样理解,Δcost/cost非常小了,就说明cost基本没啥变化,就认为已经得到一个解了,故停止优化。 -
TrustRegionStrategyType Solver::Options::trust_region_strategy_type
默认值:LEVENBERG_MARQUARDT
可选的为LEVENBERG_MARQUARDT和DOGLEG。更多细节请参考: Levenberg-Marquardt 和 Dogleg。 -
DoglegType Solver::Options::dogleg_type
默认值:TRADITIONAL_DOGLEG
可选的为TRADITIONAL_DOGLEG和SUBSPACE_DOGLEG。更多细节请参考: Dogleg。 -
bool Solver::Options::use_nonmonotonic_steps
默认值:false
更多细节请参考原文档。 -
double Solver::Options::initial_trust_region_radius
默认值:1e4
初始信任区域的大小。 当使用LEVENBERG_MARQUARDT策略时,该数字的倒数是初始正则化参数。 -
double Solver::Options::max_trust_region_radius
默认值:1e16
信任区域半径最大值。 -
double Solver::Options::min_trust_region_radius
默认值:1e-32
信任区域的最小值。当信任区域小于此值,会停止优化。 -
double Solver::Options::min_relative_decrease
默认值:1e-3
信任域步长(trust region step)相对减少的最小值。 -
double Solver::Options::min_lm_diagonal
默认值:1e6
LEVENBERG MARQUARDT算法使用对角矩阵来规范(regularize)信任域步长。 这是该对角矩阵的值的下限。 -
double Solver::Options::max_lm_diagonal
默认值:1e32
LEVENBERG MARQUARDT算法使用对角矩阵来规范(regularize)信任域步长。这是该对角矩阵的值的上限。 -
int Solver::Options::max_num_consecutive_invalid_steps
默认值:5
信任区域策略返回的步骤有时可能在数值上无效,通常是因为条件问题。 优化器可以继续尝试使用较小的信任区域/更好的条件问题来解决,而不是崩溃或停止优化。 此参数设置最小化器停止优化之前的连续重试次数。
3.3、LINE_SEARCH
-
LineSearchDirectionType Solver::Options::line_search_direction_type
默认值:LBFGS
可选的为STEEPEST_DESCENT、NONLINEAR_CONJUGATE_GRADIENT、BFGS和LBFGS,都属于LINE_SEARCH类的算法。 -
LineSearchType Solver::Options::line_search_type
默认值:WOLFE
选择是ARMIJO和WOLFE(强WOLFE条件)。 为了保证BFGS和LBFGS线搜索方向算法的基本假设得到满足,应使用WOLFE线性搜索。 -
int Solver::Options::max_lbfgs_rank
默认值:20
L-BFGS的Hessian矩阵是对Hessian矩阵的逆的低秩近似。 近似的秩的大小与近似算法的空间和时间复杂度线性相关。 秩越高,近似的质量越好。 然而,由于以下两种原因,质量的提高受到限制。
~The method only uses secant information and not actual derivatives.
~The Hessian approximation is constrained to be positive definite.
因此,将该秩增加到一个特别大的数字将大量将花费时间和空间而不会相应地提高求解的质量。不同的问题,可能最佳的秩也不同。 -
bool Solver::Options::use_approximate_eigenvalue_bfgs_scaling
默认值:false
更多细节请参考原文档。 -
LineSearchIterpolationType Solver::Options::line_search_interpolation_type
默认值:CUBIC
用于近似目标函数的多项式的次数。 可选的为BISECTION,QUADRATIC和CUBIC。 -
double Solver::Options::min_line_search_step_size
线性搜索将在满足
∥ Δ x k ∥ ∞ < min_line_search_step_size \|\Delta x_k\|_\infty < \text{min\_line\_search\_step\_size} ∥Δxk∥∞<min_line_search_step_size
时停止搜索。其中||⋅||∞是指无穷范数,Δxk是第k次迭代时参数值的step的变化量。这是线性线性搜索算法的一个终止条件。 -
double Solver::Options::line_search_sufficient_function_decrease
默认值:1e-4
完全解决线搜索问题在计算上是令人望而却步的。 幸运的是,基于行搜索的优化算法仍然可以保证收敛,如果不是精确的解决方案,行搜索算法返回一个充分降低目标函数值(cost)的解。 更准确地说,寻找步长s.t.
f ( step_size ) ≤ f ( 0 ) + sufficient_decrease ∗ [ f ′ ( 0 ) ∗ step_size ] f(\text{step\_size}) \le f(0) + \text{sufficient\_decrease} * [f'(0) * \text{step\_size}] f(step_size)≤f(0)+sufficient_decrease∗[f′(0)∗step_size]
上面的就是Armijo条件。 -
double Solver::Options::max_line_search_step_contraction
默认值: 1e-3
在线性搜索算法的每次迭代中,
new_step_size > = max_line_search_step_contraction ∗ step_size \text{new\_step\_size} >= \text{max\_line\_search\_step\_contraction} * \text{step\_size} new_step_size>=max_line_search_step_contraction∗step_size
根据定义,满足约束:
0 < max_step_contraction < min_step_contraction < 1 0 < \text{max\_step\_contraction} < \text{min\_step\_contraction} < 1 0<max_step_contraction<min_step_contraction<1 -
double Solver::Options::min_line_search_step_contraction
默认值:0.6
在线性搜索算法的每次迭代中,
new_step_size < = min_line_search_step_contraction ∗ step_size \text{new\_step\_size} <= \text{min\_line\_search\_step\_contraction} * \text{step\_size} new_step_size<=min_line_search_step_contraction∗step_size
根据定义,满足约束:
0 < max_step_contraction < min_step_contraction < 1 0 < \text{max\_step\_contraction} < \text{min\_step\_contraction} < 1 0<max_step_contraction<min_step_contraction<1 -
int Solver::Options::max_num_line_search_step_size_iterations
默认值:20
每次线搜索期间的最大试验步长迭代次数,如果在此次试验次数内无法找到满足搜索条件的步长(step size),则线性搜索将停止。
由于这是一个“人为”约束,如果正在使用WOLFE线性搜索,并且在当前搜索期间找到了满足Armijo条件的的点(in < = max_num_line_search_step_size_iterations)。 然后,具有满足Armijo条件的最低函数值的步长将作为新的有效步长返回,即使它不满足强Wolfe条件。可防止优化器在次优解处提前终止。 -
int Solver::Options::max_num_line_search_direction_restarts
默认值:5
线性搜索方向算法的最大重启次数,超过此数值时,求解就停止了。 当当前算法未能产生新的下降方向时,线性搜索方向算法会重新开始。 -
double Solver::Options::line_search_sufficient_curvature_decrease
默认值:0.9
更多细节请参考原文档。 -
double Solver::Options::max_line_search_step_expansion
默认值:10.0
和Wolfe线性搜索相关。更多细节请参考原文档。
4、与线性求解器有关的参数
-
double Solver::Options::parameter_tolerance
默认值:1e-8
求解器会在
∥ x − Π ⊞ ( x , − g ( x ) ) ∥ ∞ < = gradient_tolerance \|x - \Pi \boxplus(x, -g(x))\|_\infty <= \text{gradient\_tolerance} ∥x−Π⊞(x,−g(x))∥∞<=gradient_tolerance
其中Δx是当前迭代中线性求解器(Linear Solver)计算的步长。 -
LinearSolverType Solver::Options::linear_solver_type
默认值:SPARSE_NORMAL_CHOLESKY / DENSE_QR
线性求解器的类型,用于计算Levenberg-Marquardt算法每次迭代中线性最小二乘问题的解。 如果编译Ceres时加入了SuiteSparse或CXSparse或Eigen的稀疏Cholesky分解选项,则默认为SPARSE_NORMAL_CHOLESKY,否则为DENSE_QR。 -
PreconditionerType Solver::Options::preconditioner_type
默认值:JACOBI
迭代线性求解器使用的预处理器(Preconditioner)。 默认是块Jacobi预处理器。 有效值是IDENTITY,JACOBI,SCHUR_JACOBI,CLUSTER_JACOBI和CLUSTER_TRIDIAGONAL(复杂程度依次递增)。 更多细节请参考Preconditioner。 -
DenseLinearAlgebraLibrary Solver::Options::dense_linear_algebra_library_type
默认值:EIGEN -
shared_ptr Solver::Options::linear_solver_ordering
默认值:NULL
更多细节请参考原文档。
还有很多关于求解器的参数,用的少,我懒得列了。