kd-tree : k近邻查询和范围查询

作者:DylanFrank(滔滔)
转载请注明出处 http://blog.csdn.net/dylan_frank/article/details/77934272

想象一下我们有如下两个任务:

• 我现在想骑一辆小黄车，我想查找离我最近的k辆小黄车.
• 找到百度地图中显示在屏幕上区域中的所有酒店

这两个任务均可以用kd-tree来解决
kd-tree 主要两个用途:

• 查询离某个点的最近的 k 个邻居,
• 搜索某个区域内的所有点.

后者在计算几何中称为范围查询,例如查询某个平面区域内的点的个数.

kd-tree是什么玩意儿

kd-tree就是高维平衡树……
kd-tree 是将平面点集进行一个分割，对某一个维度满足左子树和右子树的偏序关系

若你只对代码感兴趣请直接移动到文末
代码文末

建树

以二维平面为例
在根节点以某一维度对点集进行分割，比如以 x 为序将点集分割.，即找到 x 为序的中点，将它作为根节点，比它小的作为左子树，比它大的作为右子树，递归建树，不过由于 d 层是用 x 为序，所以 d+1 层以 y 为序.依次递归下去即可.

扩展到多维的情形则是:

每一层轮流选择某一维度作为切割方向，找到沿着这一方向上的中位数节点，将其作为根，递归建树则行

实例

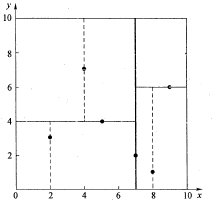
假设有6个二维数据点{（2,3），（5,4），（9,6），（4,7），（8,1），（7,2）}，数据点位于二维空间内（如图1中黑点所示）。k-d树算法就是要确定图1中这些分割空间的分割线（多维空间即为分割平面，一般为超平面）。下面就要通过一步步展示k-d树是如何确定这些分割线的。

k-NN 查找

伪代码

k_close(p,o,k,)//查询点p,树当前节点o,近邻数目k
1. 从根节点开始递归的查找，根据p在节点的左边还是右边，决定递归方向
2. 若到达叶节点,则将其作为当前最优节点
3. 回溯:
(1) 若当前节点比当前最优点更优，则将其作为当前最优节点
(2) 判断左子树是否存在最优点，若有则递归下去
4. 当根节点搜索完毕，则查找结束

实现细节

具体实现的时候需要说明的是，可以用一个优先队列存储最优的k个节点，这样每次比对回溯节点是否比当前最优点更优的时候，就只需用当前最优点中里p最远的节点来比对，而这个工作对于优先队列来说是 O(1) 的

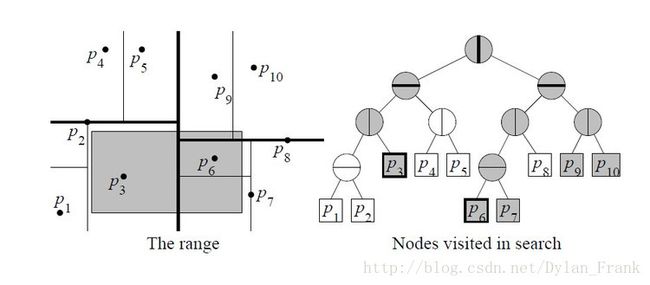
范围查询

给定一个平面矩形范围，问其中有多少个点.如图

伪代码

find(region,o)//范围，当前节点
ret =0
if 叶子节点：　ret += (o在region 内部) ,return
判断当前节点是否在范围内,在就+1
if 左子树在其内部　报告左子树内所有节点，
else 判断是否与左子树相交，若是则递归进入左子树，查询ret += (region,lc)
右子树同理

复杂度

范围查询复杂度

由于kd-tree每一层都是对平面的划分，我们考虑其孙子辈节点.查询只会对那些与其相交的节点递归查询，因此只需要判断相交区域数目就行了,
如下图

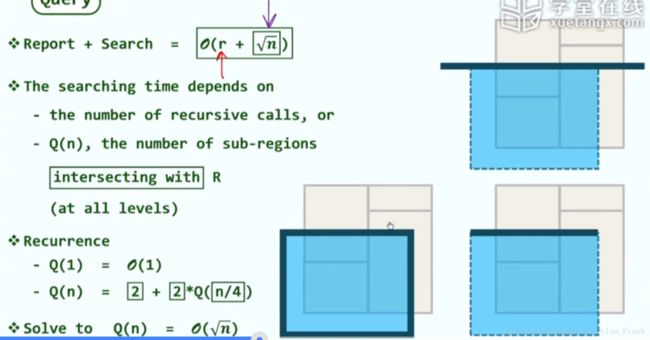
将其中一条边延展出去后至多会与两个区域相交，因此:

T(1)T(n)=O(1)=2+2T(n/4)

可以解出

T(n)=O(n−−√)

范围查询的优化

我们会发现有很多递归都是不需要的因为，有些时候某个子节点的区域已经完全包含其中了

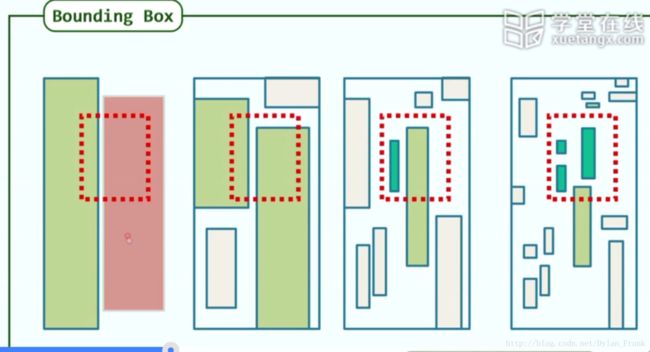
所以我们可以在节点中记录他相应管辖的区域，这样就能提前终止递归了.
详细代码见文末

超出2d

不难发现在更高纬度的时候也是一样的，我们按照每个纬度切分一次就行了,
不过复杂度会有所提高，
一般的在d维空间中进行范围查找的复杂度是 O(nd−1d) 非常高，所以不太推荐用kd-tree做范围查询，范围查询我们有更高效的数据结构—–range tree 2d的时候查询时间复杂度为 O(logn)

代码

本代码 k_close 查询经过HDU 4347 测试
那个题是在5维空间中查询k-NN,给的时限是8s

AC代码

范围查询部分，只经过个人数据测试，未在oj 测试,若有题目请联系
限于本人c++有限，设计的不够好.

int _idx;//比较维度
struct KDNode{
    const static int max_dims = 5;
    int featrue[max_dims];
    int size;//子树节点个数
    int region[max_dims][2];//每个维度最大值最小值
    int dim;
    bool operator < (const KDNode& o)const{
        return featrue[_idx]struct KDTree{
    int dims;
    KDNode Node[maxn];
    KDNode data[maxn<<2];
    bool flag[maxn<<2];
    priority_queueint,KDNode> > Q;//查询结果队列
    void build(int l,int r,int o,int dep,bool clc_region = false){
        //最后一个参数表明是否记录区域大小
        if(l>r)return;
        _idx = dep % dims;
        int lc = o<<1,rc = o<<1|1;
        flag[o] = true;
        flag[lc]=flag[rc] = 0;
        int mid = (l+r) >> 1;
        nth_element(Node+l,Node+mid,Node+r+1);
        data[o] = Node[mid];data[o].dim = _idx;
        // std::cout <<"node "<< o << '\n';
        // std::cout << _idx << '\n';
        // for(int i=0 ; i
        data[o].size = r-l+1;
        if(clc_region){
            for(int i=0 ; i0] = min_element(Node+l,Node+r+1)->featrue[i];
                data[o].region[i][1] = max_element(Node+l,Node+r+1)->featrue[i];
            }
            _idx = dep%dims;
        }
        build(l,mid-1,lc,dep+1,clc_region);
        build(mid+1,r,rc,dep+1,clc_region);
    }

    void k_close(const KDNode& p,int k,int o){
        if(!flag[o])return;
        int dim = data[o].dim;
        int lc = o<<1;int rc = o<<1|1;
        if(p.featrue[dim] >data[o].featrue[dim])swap(lc,rc);
        if(flag[lc])k_close(p,k,lc);
        pair<int,KDNode> cur(0,data[o]);
        for(int i=0 ; ibool fg = false;//右子树遍历标志
        if(Q.size() < k){
            Q.push(cur);fg =1;
        }else{
            if(cur.fi < Q.top().fi){
                Q.pop();Q.push(cur);
            }
            fg = SQ(p.featrue[dim]-data[o].featrue[dim]) < Q.top().fi;
        }
        if(flag[rc] && fg)k_close(p,k,rc);
    }
    int  check(int region[][2],int o){
        //1表示相交
        //－１表示全属于
        //0表示不相交
        if(!flag[o])return 0;
        bool fg = true;
        for(int i=0 ; iif(data[o].region[i][0] < region[i][0] || data[o].region[i][1] > region[i][1]){
                fg = false;break;
            }
        }
        int d = data[o].dim;
        return fg?-1 : data[o].region[d][1] > region[d][0] || data[o].region[d][0]1];
    }
    int find_size(int region[][2],int o){
        //查找范围内的点数
        //默认建树时有ｒｅｇｉｏｎ记录
        if(!flag[o])return 0;
        int ret =0;
        bool fg =1 ;//当前点是否在范围内
        for(int i=0 ; iif(data[o].featrue[i]0]||data[o].featrue[i]>region[i][1]){
                fg = 0;break;
            }
        ret += fg;
        int lc = o<<1,rc = o<<1|1;
        int lstate = check(region,lc),rstate = check(region,rc);
        if(lstate ==-1)ret += data[lc].size;
        else if(lstate == 1)ret += find_size(region,lc);
        if(rstate ==-1)ret += data[rc].size;
        else if(rstate == 1)ret += find_size(region,rc);
        return ret;
    }
};

局限

以上只是一颗静态树不支持加点和删除.