【Python数据挖掘课程】七.PCA降维操作及subplot子图绘制

        这篇文章主要介绍四个知识点，也是我那节课讲课的内容。
        1.PCA降维操作；
        2.Python中Sklearn的PCA扩展包；
        3.Matplotlib的subplot函数绘制子图；
        4.通过Kmeans对糖尿病数据集进行聚类，并绘制子图。

        前文推荐：
       【Python数据挖掘课程】一.安装Python及爬虫入门介绍
       【Python数据挖掘课程】二.Kmeans聚类数据分析及Anaconda介绍
       【Python数据挖掘课程】三.Kmeans聚类代码实现、作业及优化
       【Python数据挖掘课程】四.决策树DTC数据分析及鸢尾数据集分析
       【Python数据挖掘课程】五.线性回归知识及预测糖尿病实例
       【Python数据挖掘课程】六.Numpy、Pandas和Matplotlib包基础知识

        希望这篇文章对你有所帮助，尤其是刚刚接触数据挖掘以及大数据的同学，这些基础知识真的非常重要。如果文章中存在不足或错误的地方，还请海涵~

一. PCA降维

        参考文章：http://blog.csdn.net/xl890727/article/details/16898315
        参考书籍：《机器学习导论》
        任何分类和回归方法的复杂度都依赖于输入的数量，但为了减少存储量和计算时间，我们需要考虑降低问题的维度，丢弃不相关的特征。同时，当数据可以用较少的维度表示而不丢失信息时，我们可以对数据绘图，可视化分析它的结构和离群点。
        特征降维是指采用一个低纬度的特征来表示高纬度。特征降维一般有两类方法：特征选择（Feature Selection）和特征提取（Feature Extraction）。
        1.特征选择是从高纬度的特征中选择其中的一个子集来作为新的特征。最佳子集是以最少的维贡献最大的正确率，丢弃不重要的维，使用合适的误差函数进行，方法包括在向前选择（Forword Selection）和在向后选择（Backward Selection）。
        2.特征提取是指将高纬度的特征经过某个函数映射至低纬度作为新的特征。常用的特征抽取方法就是PCA（主成分分析）和LDA（线性判别分析） 。

        下面着重介绍PCA。
        降维的本质是学习一个映射函数f：X->Y，其中X是原始数据点，用n维向量表示。Y是数据点映射后的r维向量，其中n>r。通过这种映射方法，可以将高维空间中的数据点
        主成分分析（Principal Component Analysis，PCA）是一种常用的线性降维数据分析方法，其实质是在能尽可能好的代表原特征的情况下，将原特征进行线性变换、映射至低纬度空间中。
        PCA通过正交变换将一组可能存在相关性的变量转换为一组线性不相关的变量，转换后的这组变量叫主成分，它可用于提取数据的主要特征分量，常用于高维数据的降维。
        该方法的重点在于：能否在各个变量之间相关关系研究基础上，用较少的新变量代替原来较多的变量，而且这些较少新变量尽可能多地保留原来较多的变量所反映的信息，又能保证新指标之间保持相互无关（信息不重叠）。

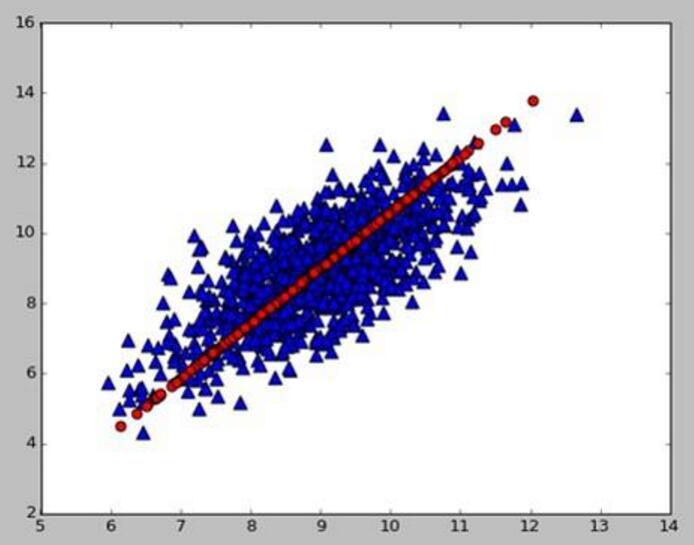
        图形解释：上图将二维样本的散点图降为一维表示，理想情况是这个1维新向量包含原始数据最多的信息，选择那条红色的线，类似于数据的椭圆长轴，该方向离散程度最大，方差最大，包含的信息量最多。短轴方向上的数据变化很少，对数据的解释能力弱。

        原理解释：
        下面引用xl890727的一张图片简单讲解，因为我数学实在好弱，恶补中。
        PCA是多变量分析中最老的技术之一，它源于通信理论中的K-L变换。

        其结果是该点到n个样本之间的距离最小，从而通过该点表示这n个样本。

        详细过程：
        下面是主成分分析算法的过程，还是那句话：数学太差是硬伤，所以参考的百度文库的，还请海涵，自己真的得加强数学。

        总结PCA步骤如下图所示：

        推荐参考资料：
        http://blog.codinglabs.org/articles/pca-tutorial.html - by: 张洋
        特征降维-PCA（Principal Component Analysis） - xl890727
        PCA的原理及详细步骤 -  百度文库

        

二. Python中Sklearn的PCA扩展包

        下面介绍Sklearn中PCA降维的方法，参考网址： http://scikit-learn.org/stable/modules/generated/sklearn.decomposition.PCA.html
        导入方法：

from sklearn.decomposition import PCA

        调用函数如下，其中n_components=2表示降低为2维。

pca = PCA(n_components=2)

        例如下面代码进行PCA降维操作：

import numpy as np
from sklearn.decomposition import PCA
X = np.array([[-1, -1], [-2, -1], [-3, -2], [1, 1], [2, 1], [3, 2]])
pca = PCA(n_components=2)
print pca
pca.fit(X)
print(pca.explained_variance_ratio_) 

        输出结果如下所示：

PCA(copy=True, n_components=2, whiten=False)
[ 0.99244291  0.00755711]

        再如载入boston数据集，总共10个特征，降维成两个特征：

#载入数据集
from sklearn.datasets import load_boston
d = load_boston()
x = d.data
y = d.target
print x[:10]
print u'形状:', x.shape

#降维
import numpy as np
from sklearn.decomposition import PCA
pca = PCA(n_components=2)
newData = pca.fit_transform(x)
print u'降维后数据:'
print newData[:4]
print u'形状:', newData.shape

        输出结果如下所示，降低为2维数据。

[[  6.32000000e-03   1.80000000e+01   2.31000000e+00   0.00000000e+00
    5.38000000e-01   6.57500000e+00   6.52000000e+01   4.09000000e+00
    1.00000000e+00   2.96000000e+02   1.53000000e+01   3.96900000e+02
    4.98000000e+00]
 [  2.73100000e-02   0.00000000e+00   7.07000000e+00   0.00000000e+00
    4.69000000e-01   6.42100000e+00   7.89000000e+01   4.96710000e+00
    2.00000000e+00   2.42000000e+02   1.78000000e+01   3.96900000e+02
    9.14000000e+00]
 [  2.72900000e-02   0.00000000e+00   7.07000000e+00   0.00000000e+00
    4.69000000e-01   7.18500000e+00   6.11000000e+01   4.96710000e+00
    2.00000000e+00   2.42000000e+02   1.78000000e+01   3.92830000e+02
    4.03000000e+00]
 [  3.23700000e-02   0.00000000e+00   2.18000000e+00   0.00000000e+00
    4.58000000e-01   6.99800000e+00   4.58000000e+01   6.06220000e+00
    3.00000000e+00   2.22000000e+02   1.87000000e+01   3.94630000e+02
    2.94000000e+00]]
形状: (506L, 13L)
降维后数据:
[[-119.81821283    5.56072403]
 [-168.88993091  -10.11419701]
 [-169.31150637  -14.07855395]
 [-190.2305986   -18.29993274]]
形状: (506L, 2L)

        推荐大家阅读官方的文档，里面的内容可以学习，例如Iris鸢尾花降维。

三. Kmeans聚类糖尿病及降维subplot绘制子图

        绘制多子图
        Matplotlib 里的常用类的包含关系为 Figure -> Axes -> (Line2D, Text, etc.)。一个Figure对象可以包含多个子图(Axes)，在matplotlib中用Axes对象表示一个绘图区域，可以理解为子图。可以使用subplot()快速绘制包含多个子图的图表，它的调用形式如下：
        subplot(numRows, numCols, plotNum)
        subplot将整个绘图区域等分为numRows行* numCols列个子区域，然后按照从左到右，从上到下的顺序对每个子区域进行编号，左上的子区域的编号为1。如果numRows，numCols和plotNum这三个数都小于10的话，可以把它们缩写为一个整数，例如subplot(323)和subplot(3,2,3)是相同的。subplot在plotNum指定的区域中创建一个轴对象。如果新创建的轴和之前创建的轴重叠的话，之前的轴将被删除。
        当前的图表和子图可以使用gcf()和gca()获得，它们分别是“Get Current Figure”和“Get Current Axis”的开头字母缩写。gcf()获得的是表示图表的Figure对象，而gca()则获得的是表示子图的Axes对象。下面我们在Python中运行程序，然后调用gcf()和gca()查看当前的Figure和Axes对象。

import numpy as np
import matplotlib.pyplot as plt
  
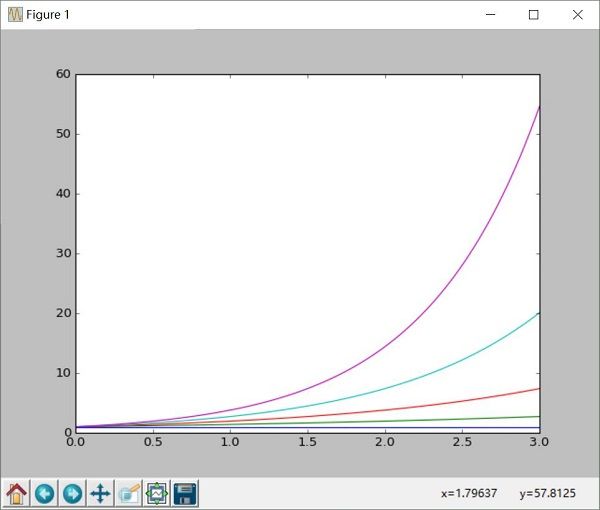
plt.figure(1) # 创建图表1
plt.figure(2) # 创建图表2
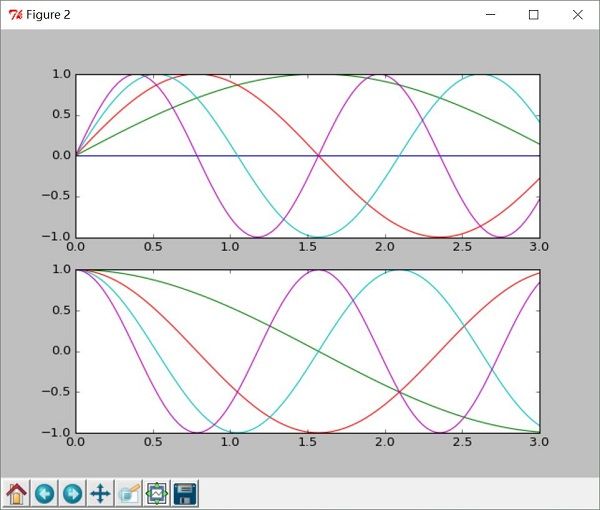
ax1 = plt.subplot(211) # 在图表2中创建子图1
ax2 = plt.subplot(212) # 在图表2中创建子图2
  
x = np.linspace(0, 3, 100)
for i in xrange(5):
    plt.figure(1)    # 选择图表1 
    plt.plot(x, np.exp(i*x/3))
    plt.sca(ax1)    # 选择图表2的子图1
    plt.plot(x, np.sin(i*x))
    plt.sca(ax2)    # 选择图表2的子图2
    plt.plot(x, np.cos(i*x))
  
plt.show()

        输出如下图所示：

    

        详细代码
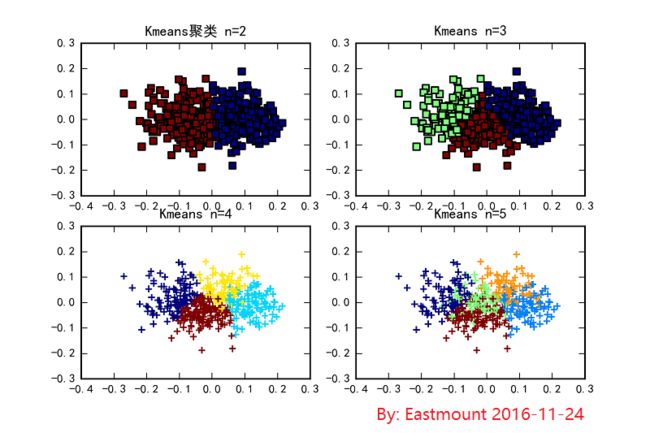
        下面这个例子是通过Kmeans聚类，数据集是load_diabetes载入糖尿病数据集，然后使用PCA对数据集进行降维操作，降低成两维，最后分别聚类为2类、3类、4类和5类，通过subplot显示子图。

# -*- coding: utf-8 -*-

#糖尿病数据集
from sklearn.datasets import load_diabetes
data = load_diabetes()
x = data.data
print x[:4]
y = data.target
print y[:4]

#KMeans聚类算法
from sklearn.cluster import KMeans
#训练
clf = KMeans(n_clusters=2)
print clf
clf.fit(x)
#预测
pre = clf.predict(x)
print pre[:10]

#使用PCA降维操作
from sklearn.decomposition import PCA
pca = PCA(n_components=2)
newData = pca.fit_transform(x)
print newData[:4]

L1 = [n[0] for n in newData]
L2 = [n[1] for n in newData]

#绘图
import numpy as np
import matplotlib.pyplot as plt

#用来正常显示中文标签
plt.rc('font', family='SimHei', size=8)
#plt.rcParams['font.sans-serif']=['SimHei'] 

#用来正常显示负号
plt.rcParams['axes.unicode_minus']=False 

p1 = plt.subplot(221)
plt.title(u"Kmeans聚类 n=2")
plt.scatter(L1,L2,c=pre,marker="s")
plt.sca(p1)


###################################
# 聚类 类蔟数=3

clf = KMeans(n_clusters=3)
clf.fit(x)
pre = clf.predict(x)

p2 = plt.subplot(222)
plt.title("Kmeans n=3")
plt.scatter(L1,L2,c=pre,marker="s")
plt.sca(p2)


###################################
# 聚类 类蔟数=4

clf = KMeans(n_clusters=4)
clf.fit(x)
pre = clf.predict(x)

p3 = plt.subplot(223)
plt.title("Kmeans n=4")
plt.scatter(L1,L2,c=pre,marker="+")
plt.sca(p3)


###################################
# 聚类 类蔟数=5

clf = KMeans(n_clusters=5)
clf.fit(x)
pre = clf.predict(x)

p4 = plt.subplot(224)
plt.title("Kmeans n=5")
plt.scatter(L1,L2,c=pre,marker="+")
plt.sca(p4)

#保存图片本地
plt.savefig('power.png', dpi=300)  
plt.show()

        输出结果如下图所示，感觉非常棒，这有利于做实验对比。

        最后希望这篇文章对你有所帮助，尤其是我的学生和接触数据挖掘、机器学习的博友。本来是24号感恩节半夜写完的，实在太累，星期六来办公室写的，同时评估终于结束了，好累，但庆幸的是好多可爱的学生，自己也在成长，经历很多终究是好事，她的酒窝没有酒，我却醉得像条狗。杨老师加油~
       (By:Eastmount 2016-11-26 下午4点半     http://blog.csdn.net/eastmount/   )