【XJOI】题解 表达式求值-逆波兰算法+字符串处理

题目链接

 

数学表达式求值：输入由数字、‘+’，‘—’，‘*’，‘/’，乘方’^’，小括号组成的字符串，输出运算结果；

 

输入格式：

一个数学表达式

 

输出格式：

运算结果，保留三位小数

 

样例输入：

样例输入一：
3*(5+3^2*(3-4)+6/2)+2.5
样例输入二：
2^0.5

 

样例输出：

样例输出一：
-0.500
样例输出二：
1.414

 

数据范围：

不会出现形如2^3^4的数据
运算的中间值不会很大
长度小于等于100

 

时间限制：

1s

 

空间限制：

64M

 

------------------------------------------------------------------------题解分割线----------------------------------------------------------------------------------

乍一看，这是一道很简单的模拟题，但当开始编码处理时就会发现，这是一道非常考验人细节处理（恶心人）的好题（毒瘤题）

那么这道题怎么做呢，初始的表达式用计算机来处理求值很显然是很困难的

那有什么好办法呢? 当然有啦，用逆波兰算法来求出表达式的后缀表达式，就可以有顺序的处理数值啦

先介绍一下逆波兰算法：（摘自网友博客）

 

逆波兰算法介绍

假定给定一个只 包含 加、减、乘、除，和括号的算术表达式，你怎么编写程序计算出其结果。

问题是：在表达式中，括号，以及括号的多层嵌套 的使用，运算符的优先级不同等因素，使得一个算术表达式在计算时，运算顺序往往因表达式的内容而定，不具规律性。 这样很难编写出统一的计算指令。
使用逆波兰算法可以轻松解决。他的核心思想是将普通的中缀表达式转换为后缀表达式。

转换为后缀表达式的好处是：
1、去除原来表达式中的括号，因为括号只指示运算顺序，不是完成计算必须的元素。
2、使得运算顺序有规律可寻，计算机能编写出代码完成计算。虽然后缀表达式不利于人阅读，但利于计算机处理。

 

算术表达式的组成部分

一个表达式有如下及部分元素组成

• 操作数：可以是任何数值：1，89 ， 3.14159 ...
• 运算符：

  分为单目运算符 如 sin , cos ， 双目运算符 如 加、减、乘、除 。

  运算符还会分为左结合性和右结合性。同级的左结合性的运算符从左往右依次计算。同级的右结合性的运算符从右往左依次计算。 
  如: 7-6+1 等价于 (7-6) + 1 ，因为普通加减运算符是左结合性的。
  如：C语言中的组合赋值语句： a = b = 1 等价于 a = (b=1) ，因为赋值运算符在C中是右结合性的。
  
  对于单目运算符，还分为前缀运算符和后缀运算符，如 sin(x) 是前缀运算符，而 阶乘运算符 ： n ! 就是后缀运算符。

 

• 分界符：一般是圆括号 ( ) ， 用于指示运算的先后顺序。

在本文中，只会考虑算术表达式 有 加、减、乘、除 运算符， 左右圆括号 ( ， ) ，合法的数字简单的情况。对于更加复杂的运算符，只要对这个算法轻微修改，就可以支持。

 

逆波兰算法的原理

逆波兰算法的核心步骤就2个：
1、将中缀表达式转换为后缀表达式，例如输入的原始表达式是 3*（5+7） ，转换得到 3 5 7 + *
2、根据后缀表达式，按照特定的计算规则得到最终结算结果

下面详细介绍这个2步的操作。

中缀表达式转换为后缀表达式
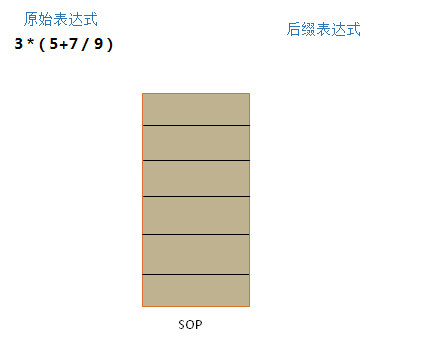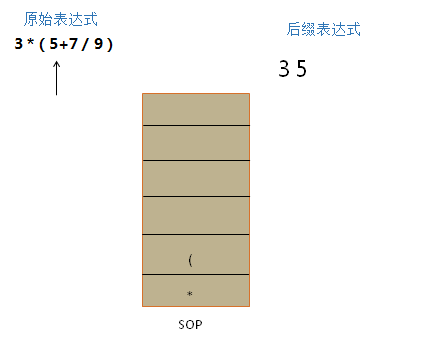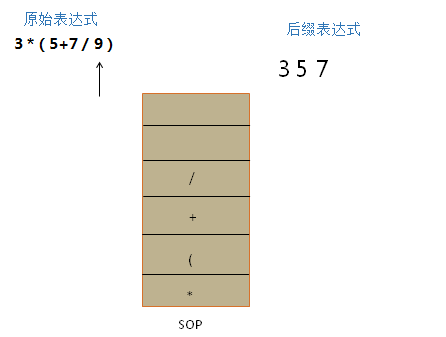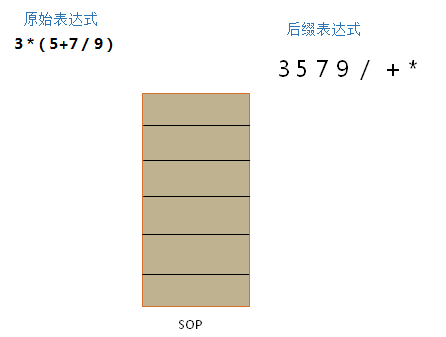
你需要设定一个栈SOP,和一个线性表 L 。SOP用于临时存储运算符和分界符( ，L用于存储后缀表达式。
遍历原始表达式中的每一个表达式元素
（1）如果是操作数，则直接追加到 L中。只有 运算符 或者 分界符（ 才可以存放到 栈SOP中
（2）如果是分界符
         Ⅰ 如果是左括号 ( ， 则 直接压入SOP，等待下一个最近的 右括号 与之配对。
          Ⅱ 如果是右括号），则说明有一对括号已经配对(在表达式输入无误的情况下)。不将它压栈，丢弃它，然后从SOP中出栈，得到元素e，将e依次追加到L里。一直循环，直到出栈元素e 是 左括号 ( ，同样丢弃他。
（3）如果是运算符（用op1表示）
        Ⅰ如果SOP栈顶元素（用op2表示） 不是运算符，则二者没有可比性，则直接将此运算符op1压栈。 例如栈顶是左括号 ( ，或者栈为空。
         Ⅱ 如果SOP栈顶元素（用op2表示） 是运算符 ，则比较op1和 op2的优先级。如果op1 > op2 ，则直接将此运算符op1压栈。
如果不满足op1 > op2，则将op2出栈，并追加到L，重复步骤3。
也就是说，如果在SOP栈中，有2个相邻的元素都是运算符，则他们必须满足：下层运算符的优先级一定小于上层元素的优先级，才能相邻。

最后，如果SOP中还有元素，则依次弹出追加到L后，就得到了后缀表达式。

 

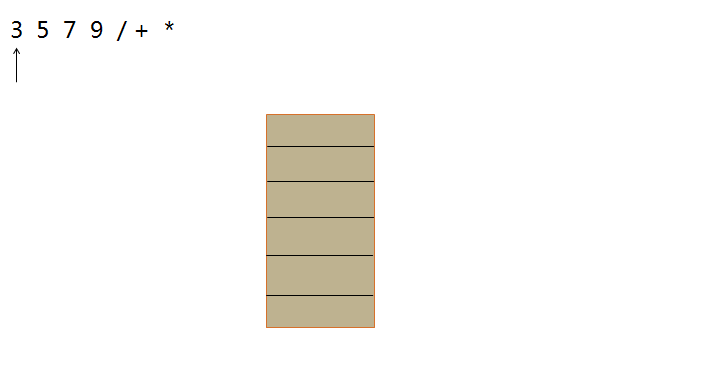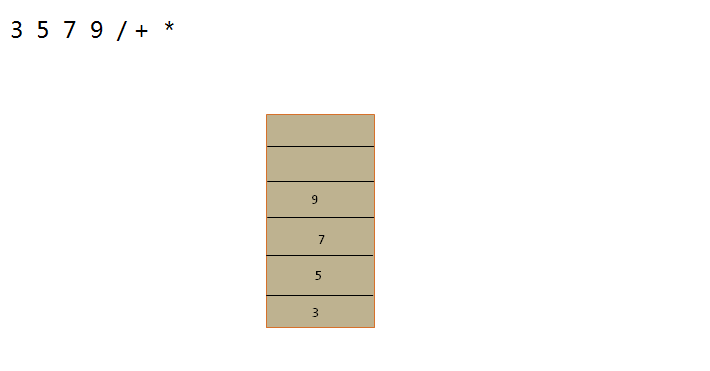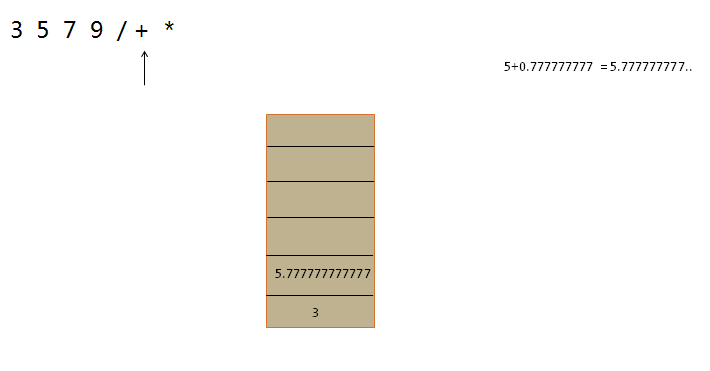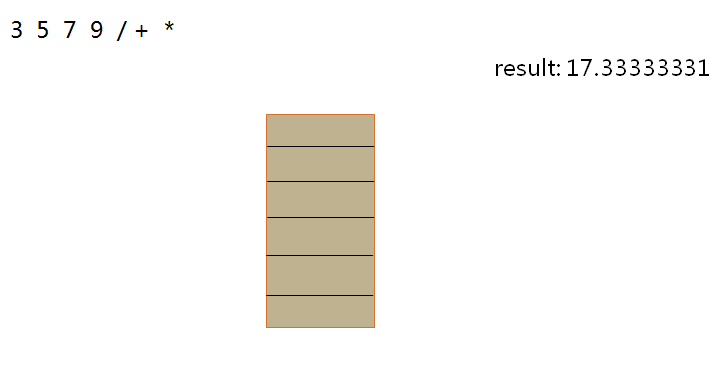
根据后缀表达式计算得到最终结果

 

执行这步操作时，也需要一个栈scalc，用于存放计算中的操作数。

 

示例图

 

如此我们就可以将一个人类读得懂机器读不懂的算术表达式转换为有顺序的规则严谨的机器操作步骤

那么这道题就解决了

PS.这道题需要耐心的慢慢打，千万别求快，中间的小错误是很难发现的，尽量一次打好，不然调试过程会让你很难过

------------------------------------------------------------------------AC代码分割线------------------------------------------------------------------------------

AC代码：

#include 
#include 
#include 
#include 
#include 
#include 
#define double long double
using namespace std;

int flag = 0;
string s;
stack  q;
stack  sop;
queue  calc;

int main ()
{
	cin >> s;
	s += '$';
	int len = s.length();
	q.push(0);
	for (int i = 0; i < len + 1; ++i)
	{
		if (s[i] >= '0' && s[i] <= '9')
		{
			double x = s[i] - '0';
			int now = i + 1;
			for (; s[now] >= '0' && s[now] <= '9' && now <= len - 1 ;)
				x = x * 10 + (s[now] - '0'), ++now;
			if (s[now] == '.')
			{
				++now;
				int cnt = 1;
				for (; s[now] >= '0' && s[now] <= '9' && now <= len - 1;)
					x = x + (double)(s[now] - '0') / (double)pow (10, cnt), ++now, ++cnt;
			}
			i = now - 1;
			q.push(x);
			continue;
		}
		else if (s[i] == '+' || s[i] == '-' || s[i] == '*' || s[i] == '/' || s[i] == '^')
		{
			int num, numm;
			if (s[i] == '+' || s[i] == '-')
				num = 1;
			else if (s[i] == '*' || s[i] == '/')
				num = 2;
			else if (s[i] == '^')
				num = 3;
			if (sop.empty())
				sop.push(s[i]);
			else if (sop.top() == '(')
				sop.push(s[i]);
			else
			{
				char x = sop.top();
				if (x == '+' || x == '-')
					numm = 1;
				else if (x == '*' || x == '/')
					numm = 2;
				else if (x == '^')
					numm = 3;
				for (; numm >= num ;)
				{
					sop.pop();
					calc.push(x);
					if (sop.empty())
						break;
					numm = 0;
					x = sop.top();
					if (x == '+' || x == '-')
						numm = 1;
					else if (x == '*' || x == '/')
						numm = 2;
					else if (x == '^')
						numm = 3;
				}
				sop.push(s[i]);
			}
		}
		else if (s[i] == '(')
			sop.push(s[i]);
		else if (s[i] == ')')
		{
			char x = sop.top();
			for (; x != '(' ;)
			{
				calc.push(x);
				sop.pop();
				x = sop.top();
			}
			sop.pop();
		}
		for (; !calc.empty() ;)
		{
			char x = calc.front();
			calc.pop();
			double a = q.top();
			q.pop();
			double b = q.top();
			q.pop();
			if (x == '+')
				q.push(a + b);
			else if (x == '-')
				q.push(b - a);
			else if (x == '*')
				q.push(a * b);
			else if (x == '/')
				q.push(b / a);
			else if (x == '^')
				q.push(pow (b, a));
		}
	}
	for (; !sop.empty() ;)
	{
		char x = sop.top();
		sop.pop();
		calc.push(x);
	}
	for (; !calc.empty() ;)
	{
		char x = calc.front();
		calc.pop();
		double a = q.top();
		q.pop();
		double b = q.top();
		q.pop();
		if (x == '+')
			q.push(a + b);
		else if (x == '-')
			q.push(b - a);
		else if (x == '*')
			q.push(a * b);
		else if (x == '/')
			q.push(b / a);
		else if (x == '^')
			q.push(pow (b, a));
	}
	printf ("%.3Lf\n", q.top());
	return 0;
}