Caffe入门:对于抽象概念的图解分析
我看过很多关于Caffe的博客,虽然收益很多,但是很遗憾没有发现一片能大彻大悟融会贯通的那种,打通任督二脉的感觉;
综合很多说法,总结归纳,写出这篇小文章,尽量做到句句为精,言简意赅:
Caffe的全称:Convolutional Architecture for Fast Feature Embedding.
l Blobs:Caffe 使用 blobs 结构来存储、交换和处理网络中正向和反向迭代时的数据和导数信息,有统一的接口类型
l Layers:Layer 是 Caffe 模型和计算的基本单元
l Nets:Net 是一系列 layers 和其连接的集合
l Forward and Backward:Caffe的两条计算生命线,Forward 产生loss和输出结果;Backward产生反向梯度
l Loss:计算真实值和预测值误差,指导下一步工作,由 loss 定义待学习的任务;
l Solver:solver 协调模型的优化;
l Layer Catalogue:学习Caffe 中构建先进模型所需的各种层的功能;
l Interface:Caffe 的命令行、Python、和 MATLAB 版接口;
有了上述的基础;我们就可以深入了解这些概念之间的抽象的关系了:先给一个总体印象:
Blob包含在Layer里包含在Net里,Solver是Net的求解。(修改这部分人主要会是研究DL求解方向的)
一、Blob概念图:
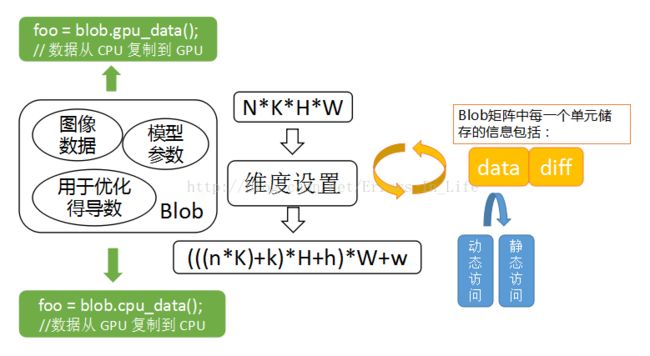
我们可以看到,图片的核心是Blob,从左往右看,Caffe 基于 blobs 存储和交换数据。为了便于优化,blobs 提供统一的内存接口来存储某种类型的数据,例如批量图像数据、模型参数以及用来进行优化的导数。
【思考:如何使得提取速度最快呢???】
Blob 使用了一个 SyncedMem 类来同步 CPU 和 GPU 上的数值,以隐藏同步的细节和最小化传送数据(绿色部分)
对于批量图像数据来说,blob 常规的维数为图像数量 N *通道数 K *图像高度 H *图像宽度 W。Blob 按行为主(row-major)进行存储,所以一个 4 维 blob 中,坐标为(n, k, h, w)的值的物理位置为: ((n * K + k) * H + h) * W + w
这也使得最后面/最右边的维度更新最快。对于 blob 中的数据,我们关心的是 values(值)和 gradients(梯度),所以一个 blob单元存储了两块数据——data 和 diff。前者是我们在网络中传送的普通数据,后者是通过网
络计算得到的梯度。(中间白色部分)
而且,由于data既可存储在 CPU 上,也可存储在 GPU 上,因而有两种数据访问方式:静态方式,不改变数值;动态方式,改变数值。(蓝色部分)
二、Blob服务于层——Layer概念图:
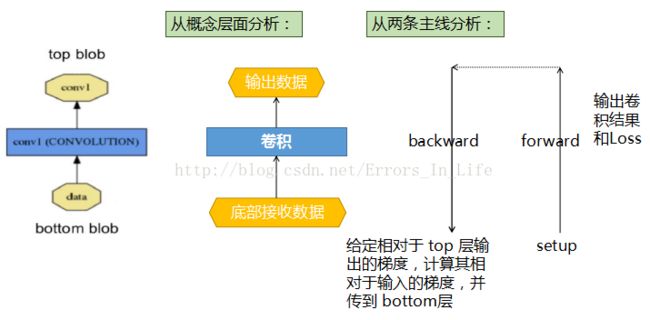
一个 layer 通过 bottom(底部)连接层接收数据,通过 top(顶部)连接层输出数据。每一个 layer 都定义了 3 种重要的运算:
setup(初始化设置),forward(前向传播),backward(反向传播)。
Setup: 在模型初始化时重置 layers 及其相互之间的连接 ;
Forward: 从 bottom 层中接收数据,进行计算后将输出送入到 top 层中;
Backward: 给定相对于 top 层输出的梯度,计算其相对于输入的梯度,并传递到 bottom层。一个有参数的 layer 需要计算相对于各个参数的梯度值并存储在内部。
有了上面可以开始定义Net了:Caffe定义了一个函数(各层前向输出)和对应梯度(各层后向输出),函数会结合各个层的输出,来计算损失函数的梯度,从而指导学习。
eg:一个典型的 Net 开始于 data layer——从磁盘中加载数据,终止于 loss layer——计算如分类和重构这些任务的目标函数。
三、Net概念图:
这里列出三个层:
图中的label就是ground truth真实值;ip就是预测值,输入到loss里面就可以实现两者的差,进而计算误差值。
前传(forward)过程为给定的待推断的输入计算输出。
在前传过程中,Caffe 组合每一层的计算以得到整个模型的计算“函数”。本过程自底向上进行。数据 x 通过一个内积层得到 g(x ),然后通过 softmax 层得到 h(g(x )),通过 softmax loss 得到 fw(x )。
反传(backward)过程根据损失来计算梯度从而进行学习。在反传过程中,Caffe 通过自动求导并反向组合每一层的梯度来计算整个网络的梯度。这就是反传过程的本质。本过程自顶向下进行。
对应的具体函数:
Net::Forward()和 Net::Backward()方法实现网络的前传和后传,
Layer::Forward()和Layer::Backward()计算每一层的前传后传。
每一层都有 forward_{cpu, gpu}()和 backward_{cpu, gpu}方法来适应不同的计算模式。(CPU 或者 GPU 模式。)
我们可以结合上面的概念图,看看下面的源代码
name: "LogReg"
layer {
name: "mnist"
type: "Data"
top: "data"
top: "label"
data_param {
source: "input_leveldb"
batch_size: 64
}
}
layer {
name: "ip"
type: "InnerProduct"
bottom: "data"
top: "ip"
inner_product_param {
num_output: 2
}
}
layer {
name: "loss"
type: "SoftmaxWithLoss"
bottom: "ip"
bottom: "label"
top: "loss"
}Caffe是端到端的机器学习引擎:Caffe 基于自己的模型架构,通过逐层定义(layer-by-layer)的方式定义一个网络(Nets)。网络从数据输入层到损失层自下而上地定义整个模型。Net的开始,就是模型(model)的开始;
首先caffe中的layers组合成为net,通过两条线来在各个layer之间运作:forward和backward,前传计算获得的是输出和损失,后传得到的是模型的梯度,与更新的权值结合,进入loss层来减少误差。
Caffe 模型的学习被分为两个部分:由 Net 计算出 loss 和 gradient,由 Solver 进行优化、更新参数。
五、什么是———Solver:
Solver 用于优化一个模型,首先通过调用前传来获得输出和损失,然后调用反传产生模型的梯度,将梯度与权值更新后相结合来最小化损失。Solver、网络和层之间的分工使得 Caffe可以模块化并且开源。
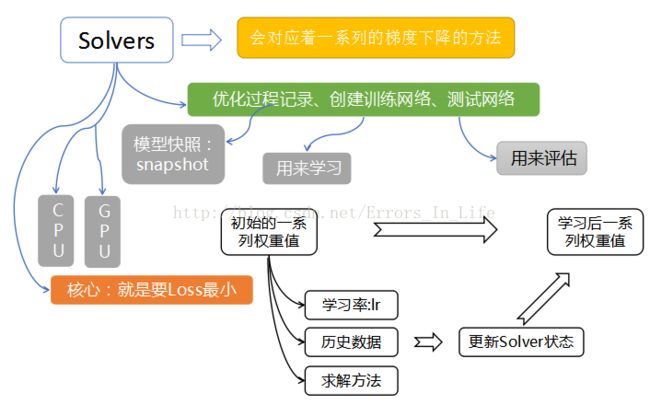
Solver概念图:
从图上看出:流程主线在黑白框,内容分支在彩色框:
1. 用于优化过程的记录、创建训练网络(用于学习)和测试网络(用于评估);
2. 通过 forward 和 backward 过程来迭代地优化和更新参数;【思考:每一次迭代发生什么?】
3. 周期性地用测试网络评估模型性能;
4. 在优化过程中记录模型和 solver 状态的快照(snapshot);
每一次迭代过称中:
1. 调用 Net 的前向过程计算出输出和 loss;
2. 调用 Net 的后向过程计算出梯度(loss 对每层的权重 w 和偏置 b 求导);
3. 根据下面所讲的 Solver 方法,利用梯度更新参数;
4. 根据学习率(learning rate),历史数据和求解方法更新 solver 的状态,使权重从初始化状态逐步更新到最终的学习到的状态。solvers 的运行模式有 CPU/GPU 两种模式。
仅仅简单介绍一种方法:随即梯度下降法(SGD):
由上图分析开始我们会发现其实并没有这么难:
随机梯度下降是通过每个样本来迭代更新一次,如果样本量很大的情况(例如几十万),那么可能只用其中几万条或者几千条的样本,就已经将W权重迭代到最优解了,对比上面的批量梯度下降,迭代一次需要用到十几万训练样本,一次迭代不可能最优,如果迭代10次的话就需要遍历训练样本10次。但是,SGD伴随的一个问题是噪音较BGD要多,使得SGD并不是每次迭代都向着整体最优化方向。
六、真实的训练会怎么设置这些参数呢?迷茫设置?——经验设置!
【设定学习率 α 和动量 μ 的经验法则】
一个比较好的建议是,将学习速率( learning rate α)初始化为α ≈ 0.01 = 102,然后在训练(training)中当 loss 达到稳定时,将 α 除以一个常数(例如 10),将这个过程重复多次。对于动量(momentum μ)一般设置为μ = 0.9,μ 使 weight 的更新更为平缓,使学习过程更为稳定、快速。
我们可以参照Caffe官方教程上面的代码来设置咯:
七、Caffe是怎么跑起来的??
这一个步骤相当重要,如果说前面是概念的理解,那么这一层就是内容上的进阶。。
因为这才是让Caffe跑起来的原理:
首先介绍一下Interface:也就是接口:Caffe 有命令行、Python 和 MATLAB 三种接口,来实现日常使用、研究代码交互以及实现快速原型。
Caffe 以 C++库为核心,其在开发中使用模块化接口而不是每次都调用其定义的编译。
cmdcaffe,pycaffe 与 matcaffe 接口都可供用户使用。
首先你要编译你的Caffe:
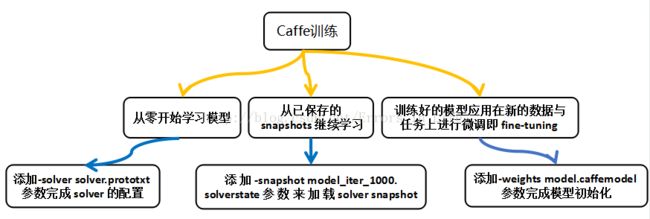
Caffe运作流程图:
到这里:Caffe的基本内容就已经介绍完了;接下来我会继续深入研究Caffe源代码,和大家交流更多的心得体会;如有遗漏请多多指出,共同进步!