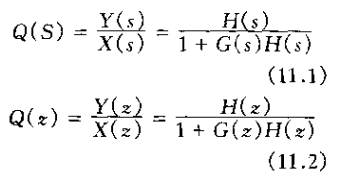《信号与系统学习笔记》—线性反馈系统(一)
注:本博客是基于奥本海姆《信号与系统》第二版编写,主要是为了自己学习的复习与加深。
一、线性反馈系统
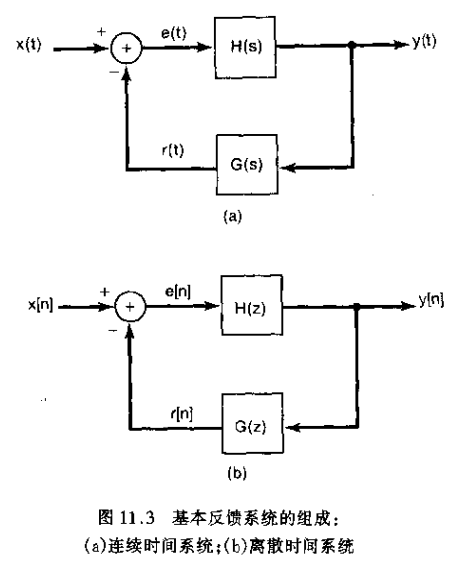
1、连续时间线性时不变反馈系统的一般结构可以用图11.3(a)所示,而离散时间线性时不变反馈系统则可以用图11.3(b)来表示
由于反馈系统最典型的应用场合都是在因果系统中,所以和那自然把图11.3(a)和图11.3(b)中的系统都局限为因果系统。图11.3中的系统函数既可以认为是单边变换,又可以认为是双边变换;而作为因果性的一个结果,其有关的收敛域,对拉普拉斯变换而言,总是位于最右边极点的右边,而对z变换而言,总是位于嘴歪层极点的外边。
2、图11.3(a)中的H(s),或图11.3(b)中的H(z)称为正向通路系统函数,而G(s)或G(z)则称为反馈通路系统函数。图11.3(a)或图11.3(b)中的整个系统函数称为闭环系统函数,特记为Q(s)或Q(z),根据图得到
式(11.1)和式(11.2)代表了研究线性时不变反馈系统的基本方程。
二、反馈的某些应用及结果
一)、逆系统设计
1、在某些应用中,希望给出一个已经连续时间系统的逆系统,嘉定西系统的系统函数为P(s),现考虑图11.4所示的反馈系统。应用式(11.1),若H(s)=K且G(s)=P(s),可求得比环刺痛函数为
若增益K足够大,因而满足KP(s)>>1,那么
式(11.4)的结果要求增益K足够大,否则它就与增益的具体大小有关。各种运算放大器就是具有这样一种增益特性的器件。在求出一个非线性系统的逆系统时,一般也采用这一基本途径。
二)、非理想元件的补偿
1、反馈的另一种应用是校正正坏系统的某些非理想特性。具体而言,开来一个开环频率响应H(jw),H(jw)在某一得定频带内有放大,但不是常数。将G(s)宣威常数没这事闭环频率响应是
若在给定频带内有
那么
根据式(11.7)可见,若闭环系统能提供一个比1大的增益,K就必须小于1.也就是说,G(jw)在给定的频率范围内必须是一个衰减器。一般来说,实现一个具有近似平坦频率特性的衰减器比实现一个具有同样频率特性的放大器来说要容易得多。应用反馈可使频率响应平坦,这是要付出代价的,由式(11.6)和式(11.7)可见
因此比环增益1/K远小于开环增益|H(jw)|。
三)、不稳定系统的稳定
1、反馈的一个重要应用是稳定一个原先在没有反馈时不稳定的系统。
2、对于利用反馈来稳定不稳定的系统,这种方法有比例反馈系统和比列加微分反馈系统。
四)、采样数据反馈系统
1、离散时间反馈级数在设计连续时间系统的各种应用中也是很重要的。数字系统的灵活性已经使采样数据反馈系统的实现具有极大的吸引力。在这样的系统中,连续时间系统的输出被采样,然后对采样的序列完成一些处理,这样就等到了已反馈控制的离散序列。然后又将这个序列变换成连续时间信号反馈到输入端,并从外部输入中减去这一反馈信号,从而产生该连续时间系统的真正输入。
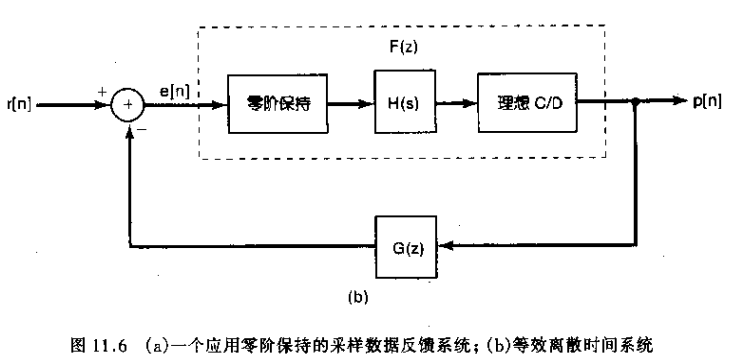
2、采样数据反馈系统在广泛的应用是零阶保持。其图示如11.6所示
图中包括一个连续时间线性时不变系统,其系统函数为H(s),它的输出y(t)被采样仪产生一个离散时间序列
然后,序列p[n]被系统函数为G(z)的离散时间线性时不变系统所处理,其输出通过一个零阶保持产生连续时间信号
这个信号由从外部输入x(t)中减去而得到e(t)。假设x(t)在T的区域内时常数,即
其中r[n]是一个离散时间序列。因为采样率一般都很高,以至于x(t)在T的区间呢没有明显变化,所以在时间中这种近似通常都是成立的。此外,在很多应用中,这个外部输入x(t)本身就是在某一离散时间序列上应用零阶保持而产生。
图11.6(b)中,输入为e[n]和输出为p[n]的离散时间系统是一个系统函数为F(z)的线性时不变系统,该系统函数F(z)与连续时间系统函数H(s)的关系是通过一种阶跃响应不定的变换连续起来的。也就是说,若s(t)是该连续时间系统的阶跃响应,那么该离散时间系统的结余响应q[n]就由s(t)的等间隔样本组成,其数学表示是
一旦去确定了F(z),就由一个完整的离散时间反馈系统的模型。
五)、跟踪系统
反馈的中药应用之一是设计一个旨在使输出跟踪输入的系统。在范围广泛的各种稳定提中,跟踪是一个重要的部分。
六)、反馈引起的不稳定
反馈也会有一些不希望的后果,事实上反馈可以引起不稳定。
三、线性反馈系统的根轨迹分析法
一)、一个例子
1、极点的轨迹值决定于正向通路和反馈通路系统函数的代数表示式,而与该系统是否是一个连续时间系统或离散时间系统无关。然而,对所得结果的解释则与连续时间系统或离散时间系统有密切关系。在离散时间情况下,重要的是极点位置与单位圆的关系;而在连续时间情况下,急死俺位置相对于虚轴的关系则很重要。
二)、闭环极点方程
1、对于较为复杂的系统,不能期望对闭环极点能找到这样简单的闭式表示式。然而,不用真正地求出任何一个具体增益值得极点位置,仍可能准确地勾画出当增益参数值从-∞到+∞变化时极点的轨迹。确定根轨迹的这一方法对了解一个反馈系统的特性是记为有用的。一旦确定了根轨迹,就有一个相当直接的办法来确定增益参数值,以沿根轨迹在任何给定位置上产生一个闭环系统。
三)、根轨迹的端点:K=0和|K|=∞时的比环极点
或许对于根堆积来说,特别是对K=0,这个方程的解必定是G(s)H(s)的极点,因为1/K=∞。
四)、角判据
1、比环系统的根轨迹,即K从-∞到+∞变化时,对某些K值来说,在复平面s内时闭环极点的那些点的集合,就是满足角条件的那些点。于是可以归纳如下:
1)、满足
的点s0位于个你轨迹上,并且对K>0的某个值来说是一个闭环极点,使s0称为闭环极点的增益值由式(11.52)确定。
2)、满足
的点s0位于根轨迹上,并且对于K<0的某个值来说是一个比环极点,使s0称为闭环极点的增益值由式(11.55)确定。
五)、根轨迹的性质
1、性质一;对于K=0,式(11.45)的解就是G(s)H(s)的极点。因为嘉定由n个极点,因此根轨迹就有n个分支,其中每一个分支都始于G(s)H(s)的一个极点(K=0)。
2、性质二;随着|K|→∞,根轨迹的每一分支都趋于G(s)H(s)的一个零点。因为假设m≤n,所以这些零点中的(n-m)个无限远点。
3、性质三;位于G(s)H(s)的奇数个实极点和零点左边的实轴部分在K>0时的根轨迹图上;位于G(s)H(s)的偶数个(包括零个)实极点和零点左边的实轴部分在K<0时的根轨迹图上。
4、性质四;当|K|足够大时,两个极点之间的轨迹必然分裂而进入复平面。