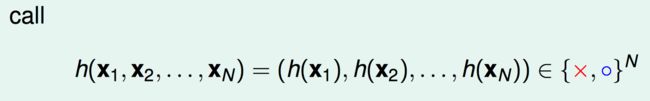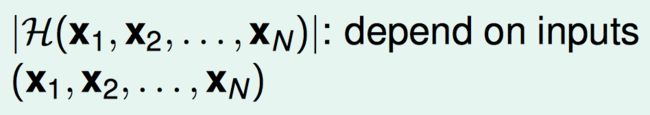机器学习基石 5.3 Effective Number of Hypotheses

1. Dichotomies: Mini-hypotheses

原来的hypothesis set：

引入新概念：

dichotomy：只关注hypothesis作用在${\mathbf{x}}_1,{\mathbf{x}}_2,\cdots ,{\mathbf{x}}_{\mathbf{N}}$上的结果，这样就可以把所有的hypothesis像上一节一样进行分类。

令
$h({\mathbf{x}}_1,{\mathbf{x}}_2,\cdots ,{\mathbf{x}}_{\mathbf{N}})=(h({\mathbf{x}}_1),h({\mathbf{x}}_2),\cdots ,h({\mathbf{x}}_{\mathbf{N}}))\in \{\times ,◯{\}}^N$

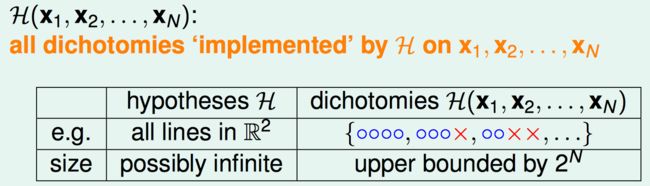
希望可以用$|\mathcal{H}({\mathbf{x}}_1,{\mathbf{x}}_2,\cdots ,{\mathbf{x}}_{\mathbf{N}})|$来代替原来的$M$。

2. Growth Function

然而$|\mathcal{H}({\mathbf{x}}_1,{\mathbf{x}}_2,\cdots ,{\mathbf{x}}_{\mathbf{N}})|$与输入的$({\mathbf{x}}_1,{\mathbf{x}}_2,\cdots ,{\mathbf{x}}_{\mathbf{N}})$有关。

用其最大值来摆脱输入的依赖。

比如：
$m_H(1)=2$
$m_H(2)=4$
$m_H(3)=8$
$m_H(4)=14$

3. Growth Function for Positive Rays

考虑一个简单的情况：Positive Rays
$$h(x)=\{\begin{array}{ll}1,& x>threshold\\ -1,& x⩽threshold\end{array}$$

相当于一维的perceptrons的一半。

易得

$\mathcal{H}({\mathbf{x}}_1,{\mathbf{x}}_2,\cdots ,{\mathbf{x}}_{\mathbf{N}})$中每一个$h({\mathbf{x}}_1,{\mathbf{x}}_2,\cdots ,{\mathbf{x}}_{\mathbf{N}})$的样子

当$N$很大时，$N+1$远小于$2^N$。

4. Growth Function for Positive Intervals

考虑另外一种情况：Positive Intervals
范围内为+1，范围外为-1。

它的$m_H(N)$

$N$个点把数轴分为$N+1$段，如果范围的两个端点放在不同的段内，那么一共有$
\begin{pmatrix}
N+1 \
2 \
\end{pmatrix}
$种，如果放在同一段内，那么只有1种。

$\mathcal{H}({\mathbf{x}}_1,{\mathbf{x}}_2,\cdots ,{\mathbf{x}}_{\mathbf{N}})$中每一个$h({\mathbf{x}}_1,{\mathbf{x}}_2,\cdots ,{\mathbf{x}}_{\mathbf{N}})$的样子

这个结果在$N$很大时也是远小于$2^N$的。

5. Growth Function for Convex Sets

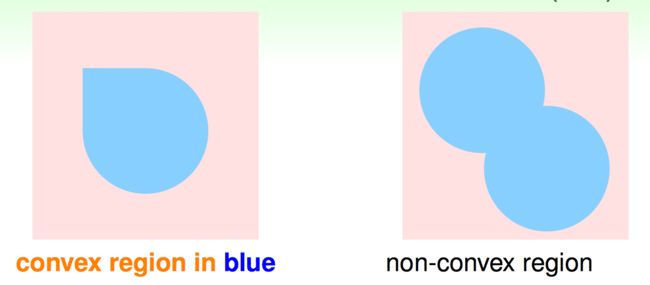
考虑$h$为平面上的一个凸包的情况

当$\mathbf{x}$在凸包内部时，$h(\mathbf{x})=1$，否则$h(\mathbf{x})=-1$

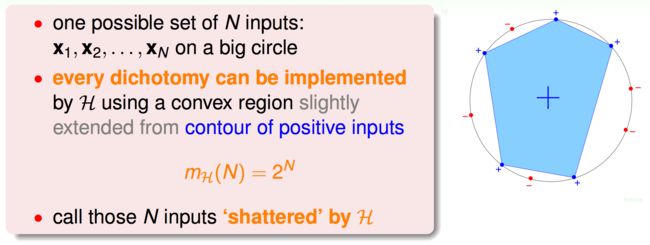
一种可能的输入：所有的点都在一个大圆上。

这时无论每个点对应的是圈还是叉，都能找到一种凸包对应一个dichotomy。

6. Fun Time