皮尔逊相关度欧式距离以及曼哈顿距离

前言

　　有些时候我们需要获得一些事物的相似度评价值，例如我们可以获取到大量的数据用以分析人们在品味方面的相似度，为此，我们可以将没个人与所有其他人进行对比，并计算他们的相似度评价。有很多种方法能够帮助我们来实现这个目的，而我们今天要提到的则是欧几里得距离和皮耶尔逊相关度，同时作为引申，简单地涉及一些曼哈顿距离的算法。

欧几里德距离

　　计算相似度评价值的一个非常简单的方法是使用欧几里德距离的评价方法，因为很多人都用了那个书上的例子，但是如果没看过这本书的人没有看前面的介绍可能理解起来也不那么舒服，因为这个算法本身很简单所以在此我使用一个更简单的图来解释一下这个 算法。下面这个图 是对两种性格的评价，一共有四个人对此作出了评价，A,B,C,D。图上很明显的表现出来了。
　　
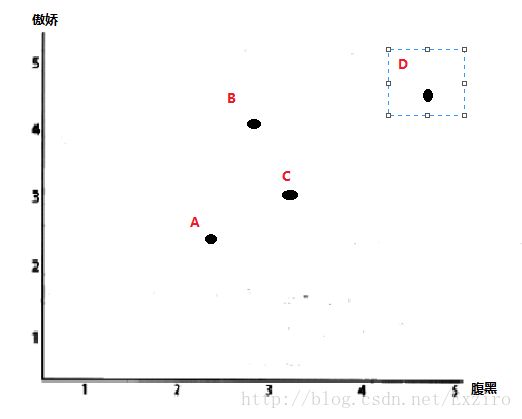
　　那么我们如何判断这些人对一些性格的相关度呢？这里的欧几里得算法其实质就是一个简单粗暴的方法。我们简单看一下这个算法的定义：1欧几里得度量（euclidean metric）（也称欧氏距离）是一个通常采用的距离定义，指在m维空间中两个点之间的真实距离，或者向量的自然长度（即该点到原点的距离）。在二维和三维空间中的欧氏距离就是两点之间的实际距离。对，其实说白了就是两个点之间的距离。（当然，这里我们所说的仅限于二维和三维空间）。
　　
　　以上就是其公式。使用欧几里得算法要注意的有一点的是，在使用欧几里得距离时需要十分注意不能对不同单位的量度使用，比如常见的容易混淆的身高体重之类。
　　下面是其实现的代码：

from math import sqrt#需要使用开方

def sim_distance(prefs,person1,person2)
si = {}#准备一个列表
for item in prefs[person1]:
   if item in prefs[person2]:
     si[item] = 1
if len(si) == 0: return 0#两者没有共同之处，返回0

sum_of_squares = sum([pow(prefs[person1][item]-pow(prefs[person2][item],2) for item in prefs[person1] if item in prefs[person2]])

return 1/(1+sqrt(sum_of_squares))

这里可能有些童鞋比较犹豫我的最后一步为什么要加1求倒数，这是因为我们得到的是距离啊（敲黑板）并不是相似度，而这里的函数值加一则是因为避免遇到点重合然后除零报错的问题。同时，由于求导，我们计算出的结果与1相近则相似度较大，与0相近则相似度较小甚至木有。

缺点：会出现较大的误差，尤其是在处理一些主观问题上时，相似度的比较误差会很大，就比如上图中的D点和A点，在我们使用欧几里得算法的时候，直观上来讲，他们的相似度会因为距离遥远而变得很低，但实际情况是，两个人的评价可能存在保守与非保守的情况，这就是一个很大的主观因素，如果你继续往下去看会发现，两人处于同一条直线，用皮尔逊相关度来解释就会发现两者的关系其实存在很大的相似度。

---

皮尔逊相关度

　　除了欧几里德距离，还有一种更复杂一些的算法可以用来判断人们兴趣的相似度，那就是皮尔逊相关系数，皮尔逊相关系数是判断两组数据与某一直线拟合程度的一种度量。对应的公式相较于欧几里德距离评价的计算公式要复杂。但是同时，同时它在数据不是很规范的时候，尤其是上述的一些主观因素时，会倾向于给出一些更好的结果。
　　假设有两个变量X、Y，那么两变量间的皮尔逊相关系数可通过以下公式计算：
　　
　　
　　
　　
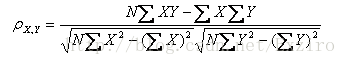
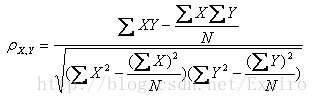
　　这四个公式是目前搜集到的四种公式，均可根据情况代入。其中E是数学期望，cov表示协方差，N表示变量取值的个数。
　　为了更加形象的说明这一方法，我们使用一个图标来举例说明，这里我们使用集体智慧书中的一个实例。随机选取了两名观影者对于相同的五部的电影的得分情况来进行说明 我们把数据放到坐标中进行比较。横纵坐标各代表一名影评者对相同电影的得分情况。
　　
　　在图上我们可以看到一条直线，绘制这条直线的原则是尽可能地靠近图上的所有坐标点，所以这条线被我们称作最佳拟合线。如果两位评论者对所有影片的评分都情况都相同，那么这条直线将成为对角线，并且会与图上所有点都相交，从而得到一个结果为1的极度理想的相关度评价。
　　我们这里的代码，使用的是来自书上的一组代码，所以它接受的参数一个列表。这部分代码首先会找出两位评论者都曾评价过的物品，然后计算两者的评分总和与平方和，并求得评分的乘积之和。不过，不同于距离度量法，这一公式不是非常的直观，但是通过除以所有变量的变化值相乘后的到的结果。它的确能够告诉我们变量的总体变化情况。

critics = {'Lisa Rose': {'Lady in the Water': 2.5, 'Snakes on a Plane': 3.5,  
                         'Just My Luck': 3.0, 'Superman Returns': 3.5, 'You, Me and Dupree': 2.5,  
                         'The Night Listener': 3.0},  
           'Gene Seymour': {'Lady in the Water': 3.0, 'Snakes on a Plane': 3.5,  
                            'Just My Luck': 1.5, 'Superman Returns': 5.0, 'The Night Listener': 3.0,  
                            'You, Me and Dupree': 3.5},  
           'Michael Phillips': {'Lady in the Water': 2.5, 'Snakes on a Plane': 3.0,  
                                'Superman Returns': 3.5, 'The Night Listener': 4.0},  
           'Claudia Puig': {'Snakes on a Plane': 3.5, 'Just My Luck': 3.0,  
                            'The Night Listener': 4.5, 'Superman Returns': 4.0,  
                            'You, Me and Dupree': 2.5},  
           'Mick LaSalle': {'Lady in the Water': 3.0, 'Snakes on a Plane': 4.0,  
                            'Just My Luck': 2.0, 'Superman Returns': 3.0, 'The Night Listener': 3.0,  
                            'You, Me and Dupree': 2.0},  
           'Jack Matthews': {'Lady in the Water': 3.0, 'Snakes on a Plane': 4.0,  
                             'The Night Listener': 3.0, 'Superman Returns': 5.0, 'You, Me and Dupree': 3.5},  
           'Toby': {'Snakes on a Plane': 4.5, 'You, Me and Dupree': 1.0, 'Superman Returns': 4.0}}  


from math import sqrt  

def sim_pearson(prefs, p1, p2):  
    # Get the list of mutually rated items  
    si = {}  
    for item in prefs[p1]:  
        if item in prefs[p2]:  
            si[item] = 1  

    # if they are no ratings in common, return 0  
    if len(si) == 0:  
        return 0  

    # Sum calculations  
    n = len(si)  

    # Sums of all the preferences  
    sum1 = sum([prefs[p1][it] for it in si])  
    sum2 = sum([prefs[p2][it] for it in si])  

    # Sums of the squares  
    sum1Sq = sum([pow(prefs[p1][it], 2) for it in si])  
    sum2Sq = sum([pow(prefs[p2][it], 2) for it in si])  

    # Sum of the products  
    pSum = sum([prefs[p1][it] * prefs[p2][it] for it in si])  

    # Calculate r (Pearson score)  
    num = pSum - (sum1 * sum2 / n)  
    den = sqrt((sum1Sq - pow(sum1, 2) / n) * (sum2Sq - pow(sum2, 2) / n))  
    if den == 0:  
        return 0  

    r = num / den  

    return r  

　　所以综上所述就是简单的对于皮尔逊相关度的算法的一个表示。有兴趣的童鞋也可以去看看有关相关度的资料对这里加强一下理解。

---

附录：曼哈顿距离

　　曼哈顿距离的命名原因是从规划为方型建筑区块的城市（如曼哈顿）间，最短的行车路径而来（忽略曼哈顿的单向车道以及只存在于3、14大道的斜向车道）。任何往东三区块、往北六区块的的路径一定最少要走九区块，没有其他捷径。
　　
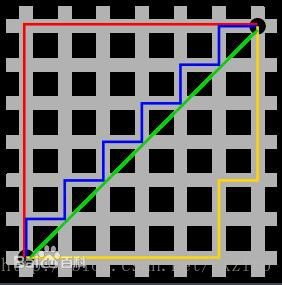
　　图中红线代表曼哈顿距离，绿色代表欧氏距离，也就是直线距离，而蓝色和黄色代表等价的曼哈顿距离。曼哈顿距离——两点在南北方向上的距离加上在东西方向上的距离，即d（i，j）=|xi-xj|+|yi-yj|。对于一个具有正南正北、正东正西方向规则布局的城镇街道，从一点到达另一点的距离正是在南北方向上旅行的距离加上在东西方向上旅行的距离，因此，曼哈顿距离又称为出租车距离。
　　在早期图形学中使用曼哈顿距离算法是因为，欧几里德算法浮点数较打且精度较低，所以使用曼哈顿距离算法。
　　

---

总结

　　在计算相似度的时候，我们可以有很多算法来选择，但是我们要根据我们的实际情况来进行选择，欧几里德算法适合快速得出相似度的时候，而皮尔逊相关度的算法则在一定程度上会更加精确。
　　以上内容经过整理得到 如有问题请及时提出感谢各位大佬。