树状数组 为何你如此优秀

想必大家对树状数组都并不陌生
近年来,许多OI赛事中都出现了它的身影.由于其编码难度较小，速度较快，受到广大Oier的喜爱(划掉)

让我们聊一聊这个神通广大的数据结构-树状数组吧!

树状数组是啥?

树状数组是一个用来维护序列的数据结构
没有啦(划水

树状数组到底是啥?

假设有这样一段序列

现在需要你支持区间查询,你会怎么做?

前缀和不就完了么 –dalao说

但是如果我们需要资瓷单点修改呢?
显然朴素前缀和的修改时间复杂度令人发指,不由得换U开核液金上倍频

所以考虑维护一个这样的序列

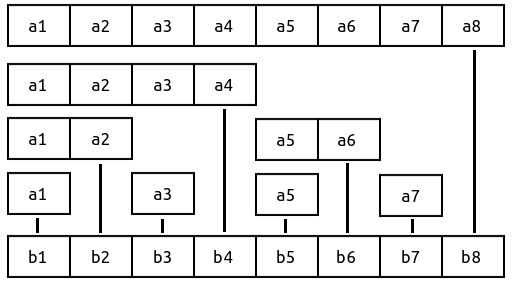
其中, a a 为原序列
* b[1]=a[1] b [ 1 ] = a [ 1 ]
* b[2]=a[1]+a[2] b [ 2 ] = a [ 1 ] + a [ 2 ]
* b[3]=a[3] b [ 3 ] = a [ 3 ]
* b[4]=a[1]+a[2]+a[3]+a[4] b [ 4 ] = a [ 1 ] + a [ 2 ] + a [ 3 ] + a [ 4 ]
* b[5]=a[5] b [ 5 ] = a [ 5 ]
* b[6]=a[5]+a[6] b [ 6 ] = a [ 5 ] + a [ 6 ]
* b[7]=a[7] b [ 7 ] = a [ 7 ]
* b[8]=a[1]+a[2]+a[3]+a[4]+a[5]+a[6]+a[7]+a[8] b [ 8 ] = a [ 1 ] + a [ 2 ] + a [ 3 ] + a [ 4 ] + a [ 5 ] + a [ 6 ] + a [ 7 ] + a [ 8 ]

与此同时,还能够写成:
* b[1]=a[1] b [ 1 ] = a [ 1 ]
* b[2]=b[1]+a[2] b [ 2 ] = b [ 1 ] + a [ 2 ]
* b[3]=a[3] b [ 3 ] = a [ 3 ]
* b[4]=b[2]+b[3]+a[4] b [ 4 ] = b [ 2 ] + b [ 3 ] + a [ 4 ]
* b[5]=a[5] b [ 5 ] = a [ 5 ]
* b[6]=b[5]+a[6] b [ 6 ] = b [ 5 ] + a [ 6 ]
* b[7]=a[7] b [ 7 ] = a [ 7 ]
* b[8]=b[4]+b[6]+b[7]+a[8] b [ 8 ] = b [ 4 ] + b [ 6 ] + b [ 7 ] + a [ 8 ]

发现了么?
当下标为 2k 2 k 时

b[2k]=∑i=12ka[i] b [ 2 k ] = ∑ i = 1 2 k a [ i ]

当下标为 2k1+2k2(k1>k2) 2 k 1 + 2 k 2 ( k 1 > k 2 ) 时

b[2k1+2k2]=∑i=2k1+12k1+2k2a[i] b [ 2 k 1 + 2 k 2 ] = ∑ i = 2 k 1 + 1 2 k 1 + 2 k 2 a [ i ]

以此类推

区间查询

显然的,将序列以这样的方式划分,能够将 a[1]−a[m] a [ 1 ] − a [ m ] 的和分为 log(m) l o g ( m ) 个块,每个块就是 b b 序列的一个节点

那么是哪 log(m) l o g ( m ) 个块呢?
假设 m=5 m = 5
那么, 5 5 的二进制表示为 101 101
这就说明将其转化为长度为 22 2 2 的块+长度为 20 2 0 的块,刚好拼成 5 5 废话

如何计算这些块的位置呢?
由图我们可知应该是
b[5]+b[4] b [ 5 ] + b [ 4 ]
将 101 101 从低位开始减,当前的数值代表着一个块的位置,最低位1的位置代表着块的长度
首先最近的是一长度为 1 1 的块 b[101] b [ 101 ]
然后减去 1 1 ,二进制变为 100 100
下一个块就是长度为 4 4 的块 b[100] b [ 100 ]
然后减去 100 100 ,二进制变为 0 0
结束

引入函数 lowbit l o w b i t
lowbit l o w b i t 函数的作用是获取一个数从二进制状态下低位到高位第一个1的位置
可以利用补码性质这么写

int lowbit(int x) {return x&(-x);}

也可以这么写

int lowbit(int x) {return x&(x^(x-1));}

所以说每次寻找下一个块时就直接

x-=lowbit(x)

完整代码

int query(int x) {
    int ans=0;
    while(x) {
        ans+=b[x];
        x-=lowbit(x);
    }
    return ans;
}

这样,就获得了 a[1]−a[m] a [ 1 ] − a [ m ] 的和
若查询 [l,r] [ l , r ] ,则 query(r)−query(l−1) q u e r y ( r ) − q u e r y ( l − 1 ) 即可

单点修改

说到修改某个位置的值,只需要看看有哪些块包含了此位置
设修改位置 m=2k1+2k2(k1>k2) m = 2 k 1 + 2 k 2 ( k 1 > k 2 ) ,包含这个块的第一个块必然是 m′=2k1+2k2+1 m ′ = 2 k 1 + 2 k 2 + 1
m′ m ′ 能够取到 2k1+1 2 k 1 + 1 到 2k1+2k2+1 2 k 1 + 2 k 2 + 1 中全部的值,刚好包括了 m m 所能取到的值,并且能够证明没有比其更小的包含当前位置的块
紧接着我们递归处理,直到块的编号超过限制为止

所以说每次寻找下一个块时就直接

x+=lowbit(x)

完整代码

void insert(int x,int add) {}
    while(x<=n) {
        b[x]+=add;
        x+=lowbit(x);
    }
}

这样,就修改了单个点值

当然,树状数组肯定不止这些用法,我会在下一篇博客中详细介绍树状数组一些使用方法,戳这里