稀疏表示（Sparse representation）原理理解

谨以此文献给我最好的朋友

我有一个十分好学的朋友，一起度过了三年的大学时光（大二认识的），最终他选择了工作，我继续读书。最近他很想了解我最近在搞的东西，在此，就发一片博客来简单说明一下自己最近研究的稀疏表示算法。因为本人能力有限，我会尽自己最大的努力将稀疏表示算法讲的清楚简单。此外，博客中避免不了会有一些差错，希望各位大佬理解。

正文

稀疏表示（Sparse Representation）也叫作稀疏编码（Sparse Coding）,就是用字典中元素的线性组合去表示测试样本。

我们现在考虑图片分类问题，如下：

现在给定一个任务，在字典中找出10张图片，用这10张图片的一个线性组合去尽可能的表示测试样本，如果是你的话，你会怎么选，你会选10张桌子图片去表示 一张狗的图片吗？不会的，你会选10张狗的图片竟可能的描述测试样本。这也就是稀疏表示的过程。表示，就是用字典中的元素（就是字典中的样本）的线性组合尽可能的描述（还原）测试样本。稀疏表示要用尽可能少的字典中的元素去描述测试样本。为什么要稀疏呢？为什么选用的字典中的样本要尽可能少呢？你可以想象对于一个狗的图片，我用大量的字典中桌子的的样本，东补补西凑凑，只要桌子的样本够多，我也是可以用大量桌子图片的线性组合去表示狗这张图片的。所以对字典中选取的样本的数量要求尽可能的少。

然后，我们的任务就是怎么将这个想法，用数学的公式表示出来，然后用计算机编程实现。

对应的数学表示

在图片分类的问题上，通常把一个两维图像，展成一个一维的向量（一般说向量，是列向量），来方便后边的操作。如何将一个二维图像展成一个一维向量呢，很简单，就是以列展开，第一列下边接上第二列，第二列下边接上第三列.....

完整之后就是这样一个情况：

下面我将详细的解释这图途中每一个字母的含义，

 表示的是第i个测试样本（就是上个图中左侧的狗这个测试样本），上边我们提到我们已经将二维图像展成了一个一维图像，在这里 为N*1的向量，N表示样本的维度。

D表示的是字典（就是上一个图中的字典），这里对字典中的每一个二维图像也展成了一个向量。D是一个N*M的矩阵，N表示样本的维度，所有的样本的维度都是相同的，用图像处理可以很简单的做到。M表示字典中训练样本的个数。

注意这个图中 的表述是不准确的，实际上应该是 ,其中 表示的是第i类训练样本的训练集，n表示类别总共n类。假设i个类别中训练样本的个数用 表示，那么可以得到n类样本总的样本个数为。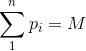

 就是对应第i个测试样本的稀疏系数。

下面我将讲明这个公式代表的具体意思（很重要），

我们把D矩阵写成行向量的形式，上个公式就变成了

注意这里的 与上边提到的 所表示的意思是不一样的， 是一个N*1的向量，表示字典中第i个元素（训练样本）,而 表示的是一个N* 的矩阵，表示的是字典中第i个训练样本的总体。

我们再把 展开，

表示列向量，我们继续变换

这个公式的含义是什么呢？你可以想仔细想想，是不是很兴奋，他代表这用的d1,d2...等训练样本去表示测试样本，这不就是我们在开头提出的问题吗？选10张照片去表示狗。

现在稀疏表示，表示已经出来了，稀疏怎么办呢，很好办，我们约束系数  是稀疏的，具体的约束就是 中非零项的个数不能超过10，用数学公式表示就是 , 这个叫做0范数，就是要求 中非零项的个数不能超过T。

最后还有一个问题怎么描述 误差呢，因为 

要做到严格的相等太难了，实际中是存在误差的，如何描述这个误差呢？

是不是已经想到办法了

最终上边所提的到的表示的问题，最终就转化成了如下公式：

arg min这个单词下边应该有一个 （CSDN的公式编辑器中没有找到如何编写），表示在s.t.的约束下，使得上个公式最小的 的值。

如何求解这个问题，我们就直接用现成的算法就好，我一般用OMP算法，具体见https://blog.csdn.net/scucj/article/details/7467955

最后最后的问题来了？怎么分类呢？？先想几分钟，其实很简单

那就是用字典中每一个类别对应的训练样本乘以与之对应的稀疏系数中的分量。

我们上边提到

现在我不这么划分了，我将D字典不按照样本数量划分了，我按照样本类别划分。

Di表示字典D中第i个类别中所有的样本， 表示Di 在系数X中对应的分量。

最终 表示用字典D中的第i类去重建测试样本  的误差。我们将误差最小的类别最为 的预测类别。

具体的流程请见：

 

 

至此本片文章结束。

但是我的朋友要求我要理论+实践，理论部分讲完了，实践部分，你们自己写吧。我觉得我讲的已经十分清楚了，这么清楚的一片博客，一个认真阅读的读者，应该可以自己写出代码来了吧

（来自朋友的一顿毒打）

所以，我还写了代码（真香），用稀疏表示来进行人脸识别（人脸分类）的。（脸好疼）

这是结果

code：code