卷积神经网络模型-LeNet-5、AlexNet、ZFNet
LeNet
LeNet由Yann LeCun在1995年完成,最初主要是用于手写数字的识别工作,它是最早的卷积神经网络之一。相比于全连接的神经网络,LeNet-5利用了卷积、参数共享、池化等操作来进行特征的提取,然后再使用全连接层进行分类,从而避免了大量的计算开销。
它的网络架构如下所示
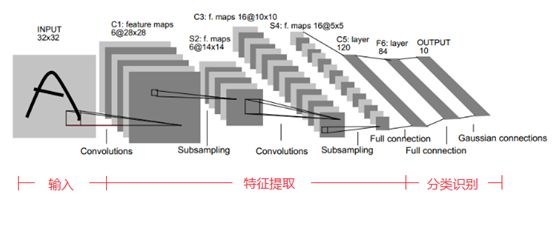
LeNet-5的具体架构设置如下所示
| 层 | 类型 | 图 | 尺寸 | 卷积核尺寸 | 步长 | 激活函数 |
|---|---|---|---|---|---|---|
| OUT | 全连接 | - | 10 | - | - | RBF |
| F6 | 全连接 | - | 84 | - | - | tanh |
| C5 | 卷积 | 120 | 1 × 1 1 \times 1 1×1 | 5 × 5 5\times 5 5×5 | 1 | tanh |
| S4 | 平均池化 | 16 | 5 × 5 5\times 5 5×5 | 2 × 2 2 \times 2 2×2 | 2 | tanh |
| C3 | 卷积 | 16 | 10 × 10 10 \times 10 10×10 | 5 × 5 5\times 5 5×5 | 1 | tanh |
| S2 | 平均池化 | 6 | 14 × 14 14 \times 14 14×14 | 2 × 2 2 \times 2 2×2 | 2 | tanh |
| C1 | 卷积 | 6 | 28 × 28 28 \times 28 28×28 | 5 × 5 5\times 5 5×5 | 1 | tanh |
| In | 输入 | 1 | 32 × 32 32 \times 32 32×32 | - | - | - |
- LeNet-5在进行手写数字识别时,输入的 28 × 28 28 \times 28 28×28的图像被零填充到 32 × 32 32 \times 32 32×32 ,而且进行了归一化处理
- 这里的池化操作不是简单的找出最大值或是平均值,而是每个神经元计算输入值,然后将结果乘以一个可学习的系数,并添加一个可学习的偏执参数,最终应用激活函数
- 大多数的C3图中的神经元指连接到S2图中的三到四个神经元
- 输出层每个神经元输出的是输入向量和权值向量之间的欧式距离,然后是每个输出衡量了该图片属于某个特定数字类的可能性
我们可以使用Keras简单的创建一个LeNet-5
def LeNet():
model = Sequential()
model.add(Conv2D(32,(5,5),strides=(1,1),input_shape= (28,28,1),padding='valid',activation='relu',kernel_initializer='uniform'))
model.add(MaxPooling2D(pool_size=(2,2)))
model.add(Conv2D(64,(5,5),strides=(1,1),padding='valid',activation='relu',kernel_initializer='uniform'))
model.add(MaxPooling2D(pool_size=(2,2)))
model.add(Flatten())
model.add(Dense(100,activation='relu'))
model.add(Dense(10,activation='softmax'))
return model
下面显示的是LeNet-5在识别手写数字3的一个过程
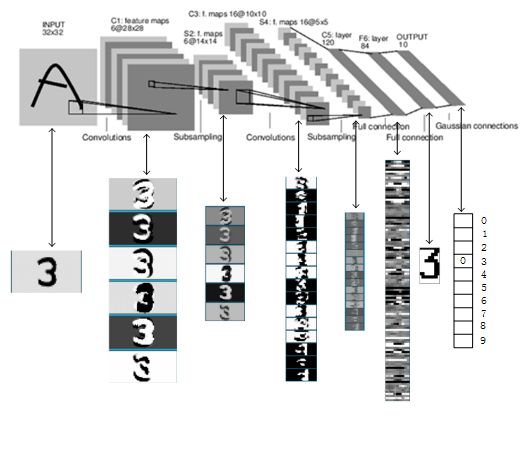
LeNet-5最重要的一点就是它基本上确定了卷积神经网络的组成,即主要包含卷积层、池化层、全连接层和激活函数。
AlexNet
2012年,Alex Krizhevsky、Ilya Sutskever在多伦多大学Geoff Hinton的实验室设计出了一个深层的卷积神经网络AlexNet,夺得了2012年ImageNet LSVRC的冠军,且准确率远超第二名(top5错误率为15.3%,第二名为26.2%),引起了很大的轰动。至此,深度学习开始逐渐成为人工智能领域一个热门的方向,它可以认为是深度学习的一个里程碑,具体可见原论文**《ImageNet Classification with Deep Convolutional Networks》**。
它的网络架构如下所示
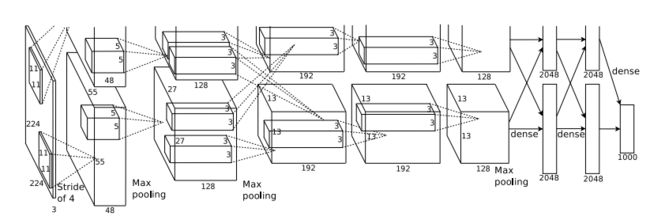
因为AlexNet在最初的训练时使用了两块GPU,所以如上图所示的它有两股流
AlexNet的具体架构如下所示
| 层 | 类型 | 特征图 | 尺寸 | 卷积核尺寸 | 步长 | 填充 | 激活函数 |
|---|---|---|---|---|---|---|---|
| OUT | 全连接 | - | 1000 | - | - | - | Softmax |
| F9 | 全连接 | - | 4096 | - | - | - | Relu |
| F8 | 全连接 | - | 4096 | - | - | - | Relu |
| C7 | 卷积 | 256 | 13 × 13 13 \times 13 13×13 | 3 × 3 3 \times 3 3×3 | 1 | SAME | Relu |
| C6 | 卷积 | 384 | 13 × 13 13 \times 13 13×13 | 3 × 3 3 \times 3 3×3 | 1 | SAME | Relu |
| C5 | 卷积 | 384 | 13 × 13 13 \times 13 13×13 | 3 × 3 3 \times 3 3×3 | 1 | SAME | Relu |
| S4 | 最大池化 | 256 | 13 × 13 13 \times 13 13×13 | 3 × 3 3 \times 3 3×3 | 2 | VALID | - |
| C3 | 卷积 | 256 | 27 × 27 27 \times 27 27×27 | 5 × 5 5 \times 5 5×5 | 1 | SAME | Relu |
| S2 | 最大池化 | 96 | 27 × 27 27 \times 27 27×27 | 3 × 3 3 \times 3 3×3 | 2 | VALID | - |
| C1 | 卷积 | 96 | 55 × 55 55 \times 55 55×55 | 11 × 11 11 \times 11 11×11 | 4 | SAME | Relu |
| In | 输入 | 3 | 224 × 224 224 \times 224 224×224 | - | - | - | - |
AlexNet包含了6亿三千万个连接,6000万个参数和65万个神经元,拥有5个卷积层,其中3个卷积层后面连接了最大池化层,最后还有3个全连接层。
训练技巧
AlexNet比较重要的一点,它使用了很多的训练技巧来提高训练的效率,以及对于结果的提升
-
Dropout:它随机忽略一部分神经元,缓解了神经网络的过拟合现象,防止对网络参数优化时陷入局部最优的问题,提高了模型的鲁棒性,主要用于最后的几个全连接层
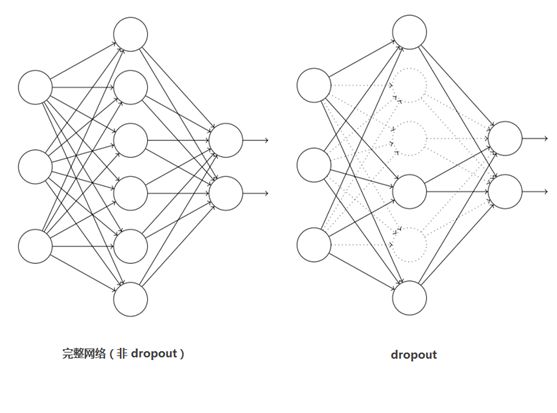
-
数据增强:通过图像平移、水平翻转、调整图像灰度等方法扩充样本训练集,使得训练得到的网络对局部平移、旋转、光照变化具有一定的不变性,数据经过扩充以后可以达到减轻过拟合并提升泛化能力

-
最大池化:避免了使用平均池化所造成的图像模糊的效果
-
激活函数:这里使用的是Relu而不是tanh,它的梯度性质更好,一定程度上缓解了梯度消失的问题,同时加快了网络的训练,降低了计算复杂度,提高了网络的鲁棒性
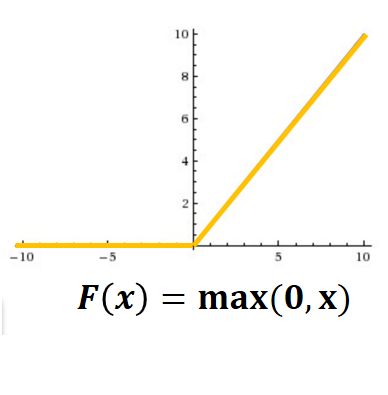
-
Local Response Normalization,LRN:即局部响应归一化处理,实际就是利用临近的数据做归一化。它一般是在激活、池化后使用。LRN是对局部神经元的活动创建竞争机制(借鉴了神经生物学上的侧抑制的概念),使得其中响应较大的值变得相对更大,并抑制其他反馈较小的神经元,从而增强了模型的泛化能力。
数学表达式如下所示
b x , y i = a x , y i / ( min ( N − 1 , i + n / 2 ) k + α ∑ j = max ( 0 , i − n / 2 ) min ( N − 1 , i + n / 2 ) ( a x , y j ) 2 ) β b_{x, y}^{i}=a_{x, y}^{i} / \left( \begin{array}{c}{\min (N-1, i+n / 2)} \\ {k+\alpha \sum_{j=\max (0, i-n / 2)}^{\min (N-1, i+n / 2)}\left(a_{x, y}^{j}\right)^{2}}\end{array}\right)^{\beta} bx,yi=ax,yi/(min(N−1,i+n/2)k+α∑j=max(0,i−n/2)min(N−1,i+n/2)(ax,yj)2)β
其中 a x , y i a_{x,y}^i ax,yi表示卷积核 i i i作用于 ( x , y ) (x,y) (x,y) 然后采用Relu计算得到的活跃度; N N N是该层卷积核的总数目; k , n , α , β k,n,\alpha,\beta k,n,α,β是超参数, k k k为偏置参数, r r r为深度半径
关于AlexNet更详细的介绍可见
https://my.oschina.net/u/876354/blog/1633143
https://blog.csdn.net/zyqdragon/article/details/72353420
ZFNet
ZFNet纽约大学Matthew Zeiler 和 Rob Fergus设计,赢得了2013的ILSVRC比赛的冠军,本质上就是AlexNet,只不过进行了某些超参数的调整,比如特征图数量、卷积核大小、步长等。它最大的贡献在于通过使用可视化技术揭示了神经网络各层到底在干什么,起到了什么作用。
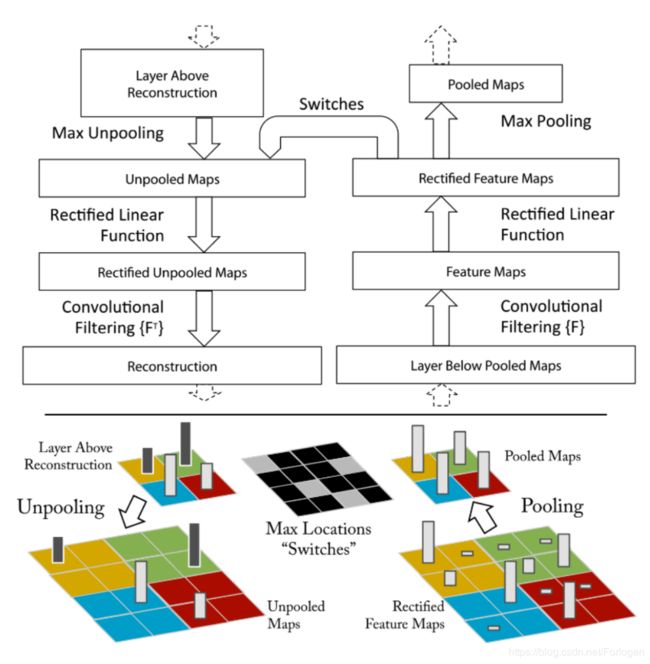
训练过程
- 反卷积可视化:一个卷积层加一个对应的反卷积层;输入是feature map,输出是图像像素;过程包括反池化操作、Relu和反卷积过程
- 反池化:从对池化的理解上我们知道,真正意义上的反池化是无法实现的,所以这里使用的是一种近似的实现,假设使用最大池化,在池化的过程中不仅要找到区域中的最大值,还要记录它的位置,这样在反池化时,就将最大值返回到它原始的位置上,其他位置写零
- Relu:根据Relu的定义可知,它保证输出的feature map总是为正数。所以在反卷积时也需要保证每一层的feature map都是正值,故这里使用Relu作为非线性激活函数
- 反卷积:这里称为反卷积其实更多的是和训练时的卷积操作对照,真正的名字是转置卷积操作。
训练细节
网络结构类似于AlexNet,有两点不同,一是将3,4,5层的变成了全连接,二是卷积核的大小减小,详细的可总结如下所示
-
AlexNet用了1500万张图像,ZFNet用了130万张图像。
-
AlexNet在第一层中使用了大小为 11 × 11 11×11 11×11的滤波器,而ZFNet使用的滤波器大小为 7 × 7 7 \times7 7×7,整体处理速度也有所减慢,但这样做有助于保留大量的原始象素信息
-
随着网络增大,使用的滤波器数量增多。
-
利用Relu将交叉熵代价函数作为误差函数,使用批处理随机梯度下降进行训练。
-
使用一台GTX 580 GPU训练了12天。
-
开发可视化技术“解卷积网络”(Deconvolutional Network),有助于检查不同的特征激活和其对输入空间关系。名字之所以称为“deconvnet”,是因为它将特征映射到像素(与卷积层恰好相反)。
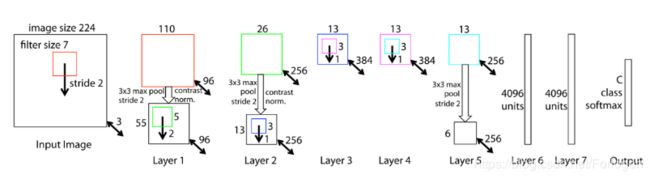
ZFNet虽然对于网络结构没有太大得调整,但它对CNN的运作机制提供了极好的直观信息,展示了更多提升性能的方法。论文所描述的可视化方法不仅有助于弄清CNN的内在机理,也为优化网络架构提供了有用的信息。
参考
https://my.oschina.net/u/876354/blog/1632862
https://cuijiahua.com/blog/2018/01/dl_3.html
https://blog.csdn.net/jiaoyangwm/article/details/80011656
https://my.oschina.net/u/876354/blog/1633143