Time Series Analysis (TSA) in Python-Linear Models to GRACH 笔记（一）

以下内容主要来自：

Time Series Analysis (TSA) in Python - Linear Models to GARCH

上面这篇post是一篇很有用处的文章，从时间序列的平稳性到线性模型，再到自回归模型以及GARCH，不仅内容比较充实，还有python的代码，所以主体是基于这篇文章，其中也加入了我自己的一些理解。

本篇目录：

Motivation

 The Basics

1、Stationarity (平稳性)

2、Serial Correlation (Autocorrelation) (自相关性)

3.Why Do We Care about Serial Correlation?(为什么要重视序列的相关性)

White Noise and Random Walks

---

Motivation

时间序列分析的技术有很多，而如何正确地使用它们，以及将它们整合则需要对它们有更深入的理解，它们都有使用的前提和条件，并不是直接将它们套用就可以了。有句话来自Michael Halls Moore (QuantStart.com 的创始人) 的一句话需要好好理解：

Time series analysis attempts to understand the past and predict the future.

通过对已经发生过的历史数据进行分析，来更好地去预测未来。包括预测未来资产收益，未来相关(correlations)/不相关性(covariances)，以及未来波动率(volatility)。

下面以对从 Yahoo Finance 中抓取的SPY(标普ETF)，TLT(美国国债20+年ETF-iShares)，MSFT(微软)从2007年1月1日到2015年1月1日这三只股票八年的收盘价进行分析。

import os
import sys

import pandas as pd
import pandas_datareader.data as web
import numpy as np

import statsmodels.formula.api as smf
import statsmodels.tsa.api as smt
import statsmodels.api as sm
import scipy.stats as scs
from arch import arch_model

import matplotlib.pyplot as plt
import matplotlib as mpl
%matplotlib inline
p = print

p('Machine: {} {}\n'.format(os.uname().sysname,os.uname().machine))
p(sys.version)

# Machine: Linux x86_64

# 3.5.2 |Anaconda custom (64-bit)| (default, Jul  2 2016, 17:53:06) 
# [GCC 4.4.7 20120313 (Red Hat 4.4.7-1)]


end = '2015-01-01'
start = '2007-01-01'
get_px = lambda x: web.DataReader(x, 'yahoo', start=start, end=end)['Adj Close']

symbols = ['SPY','TLT','MSFT']
# raw adjusted close prices
data = pd.DataFrame({sym:get_px(sym) for sym in symbols})
# log returns
lrets = np.log(data/data.shift(1)).dropna()

 The Basics

1、Stationarity (平稳性)

用一张来自 SeanAbu.com 的图片来直观理解时间序列的平稳性。

 时间序列平稳有什么意义，或者说平稳的时间序列具有哪些特征？从上图中得到：

1. 时间序列的均值（mean）不是时间的函数，或者围绕一个常数上下波动，1中红色序列的均值可以看出是随着时间而增加的，所以它不是平稳的。
2. 时间序列的方差（variance）不是时间的函数，2中红色序列的均值满足第1条但是它的方差不断扩张。
3. 时间序列的协方差（covariance）不是时间的函数，2中红色序列满足第1、2条，但是它中间部分随着时间而变得更近了，也就是说 i 项和 i+m 具有相关性。

如果保证了时间序列的平稳性，那么对未来的预测就会简单很多，因为未来数据和现在数据具有相同的统计特征（statistical properties）；另外，很多模型都是要在协方差平稳（covariance-stationarity ）的假设下的，所以只有时间序列是在稳定的情况下，通过这些模型得到的结果才是有意义的。

然而，我们分析的大多数时间序列都是不稳定的，如金融市场的时间序列。因此，我们需要首先做的检验时间序列是否是平稳的，当我们用肉眼无法判断是否平稳时，就需要借助数学工具了。平稳性检验的常用方法有 ADF(Augemented Dickey-Fuller)检验， 即单位根检验，如果不平稳再通过其他方法将它们转换为平稳的。

ADF检验即是检验序列中是否存在单位根，因为存在单位根就是非平稳时间序列了。

ADF检验过程：

以后填

---------------------------------------------------

2、Serial Correlation (Autocorrelation) (自相关性)

通常我们分析一个时间序列时，会将它分解为三个部分进行研究：

• trend (趋势)
• seasonal/cyclical (季节性/周期性)
• random (随机部分)

随机部分也叫做残差（residual）或者误差（error），它可以是预测值和观测值之间的偏差，是无法控制的，无法度量的随机项。如 ，其中X、Y是自变量和因变量，a和b是参数，而u则是作为随机扰动项。当时间序列的残差具有相关性时，那么这个序列就是自相关的。

3.Why Do We Care about Serial Correlation?(为什么要重视序列的相关性)

关系时间序列的相关性是因为它对模型预测的正确性有着重要的意义。回顾一下定义，平稳时间序列的残差是序列不相关的，后面的随机漫步和白噪声的例子可以看出。检验时间序列是否具有相关性的方法有杜宾-沃森（Durbin-Watson）检验。

D-W检验过程：

以后填

----------------------------

White Noise and Random Walks

白噪声是第一个需要理解的时间序列，根据定义知：白噪声过程的时间序列具有连续不相关的误差，并且这些误差的均值（mean）为零。并且对于连续不相关的误差的另一种描述是独立同分布（independent and identical distribution, iid）。

下面模拟了一个白噪声过程。

def tsplot(y, lags=None, figsize=(10, 8), style='bmh'):
    if not isinstance(y, pd.Series):
        y = pd.Series(y)
    with plt.style.context(style):    
        fig = plt.figure(figsize=figsize)
        #mpl.rcParams['font.family'] = 'Ubuntu Mono'
        layout = (3, 2)
        ts_ax = plt.subplot2grid(layout, (0, 0), colspan=2)
        acf_ax = plt.subplot2grid(layout, (1, 0))
        pacf_ax = plt.subplot2grid(layout, (1, 1))
        qq_ax = plt.subplot2grid(layout, (2, 0))
        pp_ax = plt.subplot2grid(layout, (2, 1))
        
        y.plot(ax=ts_ax)
        ts_ax.set_title('Time Series Analysis Plots')
        smt.graphics.plot_acf(y, lags=lags, ax=acf_ax, alpha=0.5)
        smt.graphics.plot_pacf(y, lags=lags, ax=pacf_ax, alpha=0.5)
        sm.qqplot(y, line='s', ax=qq_ax)
        qq_ax.set_title('QQ Plot')        
        scs.probplot(y, sparams=(y.mean(), y.std()), plot=pp_ax)

        plt.tight_layout()
    return 

np.random.seed(1)

# plot of discrete white noise
randser = np.random.normal(size=1000)
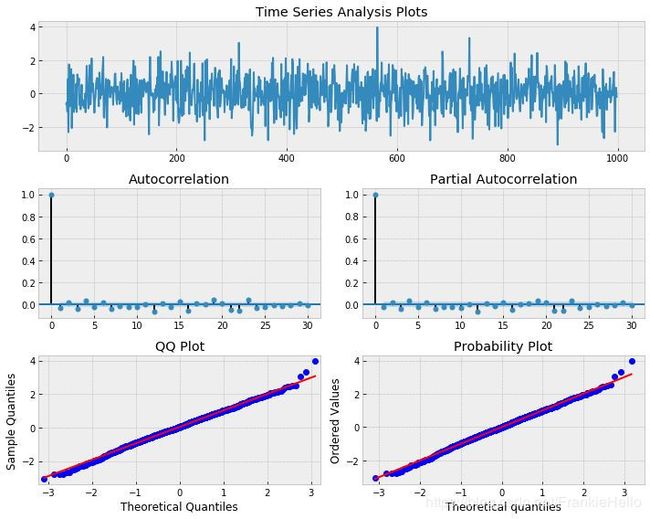
tsplot(randser, lags=30)

 

 从上图中可以看到：

• 这个过程是随机的，并且是围绕的中心是零。
• 自相关(autocorrelation, ACF)和偏自相关(partial autocorrelation, PACF)也没有表现出明显的序列相关。由于是正态分布采样，所以从自相关图中看到大约5%的显著性。
• 通过QQ（Quantile Quantile Plot）图和PP图，可以看出理论分布和实际的数据样本分布近似，所以样本数据符合正态分布。

关于PP图和QQ图： 来自 ：http://www.cnblogs.com/king-lps/p/7840268.html

   统计学里Q-Q图（Q代表分位数）是一个概率图，用图形的方式比较两个概率分布，把他们的两个分位数放在一起比较。首先选好分位数间隔。图上的点（x,y）反映出其中一个第二个分布（y坐标）的分位数和与之对应的第一分布（x坐标）的相同分位数。因此，这条线是一条以分位数间隔为参数的曲线。如果两个分布相似，则该Q-Q图趋近于落在y=x线上。如果两分布线性相关，则点在Q-Q图上趋近于落在一条直线上，但不一定在y=x线上。Q-Q图可以用来可在分布的位置-尺度范畴上可视化的评估参数。

   从定义中可以看出Q-Q图主要用于检验数据分布的相似性，如果要利用Q-Q图来对数据进行正态分布的检验，则可以令x轴为正态分布的分位数，y轴为样本分位数，如果这两者构成的点分布在一条直线上，就证明样本数据与正态分布存在线性相关性，即服从正态分布。

    P-P图是根据变量的累积概率对应于所指定的理论分布累积概率绘制的散点图，用于直观地检测样本数据是否符合某一概率分布。如果被检验的数据符合所指定的分布，则代表样本数据的点应当基本在代表理论分布的对角线上。由于P-P图和Q-Q图的用途完全相同，只是检验方法存在差异。要利用QQ图鉴别样本数据是否近似于正态分布,只需看QQ图上的点是否近似地在一条直线附近,而且该直线的斜率为标准差,截距为均值.

随机漫步的定义如下：

 从定义可以看出，随机漫步时间序列是不平稳的，因为连续两个观测值之间的协方差在时间上是相互依赖的。所以说如果时间序列是随机漫步模型，那么它将无法预测！

从标准正态分布中采样数据来模拟一段随机漫步：

# Random Walk without a drift

np.random.seed(1)
n_samples = 1000

x = w = np.random.normal(size=n_samples)
for t in range(n_samples):
    x[t] = x[t-1] + w[t]

_ = tsplot(x, lags=30)

 从图中可以明显看出随机漫步时间序列是不平稳的，但是将模型 进行移项可得 ，所以随机漫步的一阶差分是白噪声过程，所以通过 np.diff() 函数来进行一阶差分，看它是否成立。

# First difference of simulated Random Walk series

tsplot(np.diff(x), lags=30)

 确实是一个白噪声过程，由于SPY的股价走势也像一个随机漫步的过程，那么我们用随机漫步来拟合一下SPY股价的一阶差分会怎么样呢？

# First difference of SPY prices
_ = tsplot(np.diff(data.SPY), lags=30)

 

 确实很像白噪声，但是QQ图和PP图中，这个过程很像正态分布，但是存在heavy tails, 而且在ACF和PACF图中，有一些重要的序列相关性（1，5，16，18，21处），这就意味着存在着更好的模型去描述这个价格变化的过程。

 

Time Series Analysis (TSA) in Python-Linear Models to GRACH 笔记（二）