机器学习基石第二讲:Learning to Answer Yes/No
Perceptron Hypothesis Set
感知机模型:

这里 W , t h r e s h o l d W,threshold W,threshold的不同,使得 h h h也不同,所以说这模型有它的Hypothesis Set。
然后向量化感知机的表达:

形式化的理解,用几何的角度来理解:
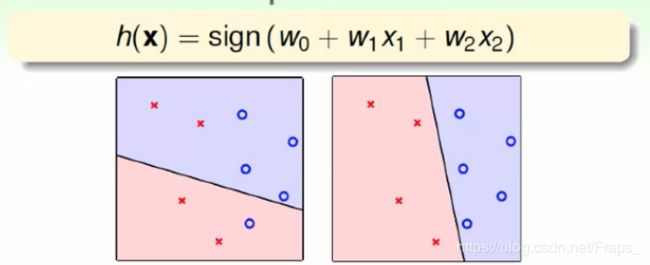
每一个感知机代表一条划分平面的一条线,用动画显示:这个放到后面去
Perceptron Learning Algorithm (PLA)
我们知道对于线性可分的数据 D D D,一定存在一条完美的线 f f f,将数据划分出来,如图表示:
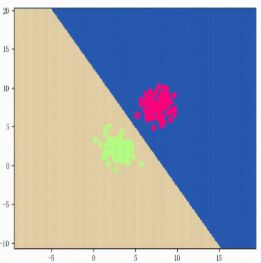
但是这个理想中的 f f f是不知道的,我们只知道这个数据和Hypothesis Set,现在的问题是如何设计一个算法,选出存在于Hypothesis Set中的一条线g,使得 g ≈ f g \approx f g≈f?
主要思路是,先随机的选出一条线 g g g,然后慢慢修正它,最终使得 g ≈ f g \approx f g≈f

如图,这个条线 g 0 , 与 之 对 应 的 权 重 是 向 量 W 0 g_0,与之对应的权重是向量W_0 g0,与之对应的权重是向量W0 g 0 g_0 g0发现了一个错误分类,然后向那边移动,修正这个错误,如此循环,直到消除所有错误。算法的流程如下:

这里的 t t t代表轮次, y = 1 或 − 1 y=1 或-1 y=1或−1,在每一轮里面,算法找到一个错误点,然后通过第二步修正这个错误,如此一轮一轮的迭代,最终使得不犯错误。
下面解释第二步中的修正公式:
当 y = 1 y=1 y=1时出错,说明 W W W与 X X X的夹角大于 9 0 0 90^0 900,那我们就减小他们的角度:
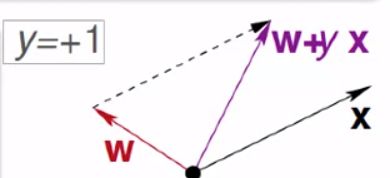
同理,当 y = − 1 y=-1 y=−1时出错,说明 W W W与 X X X的夹角小于 9 0 0 90^0 900,那我们就增加他们的角度:

Guarantee of PLA
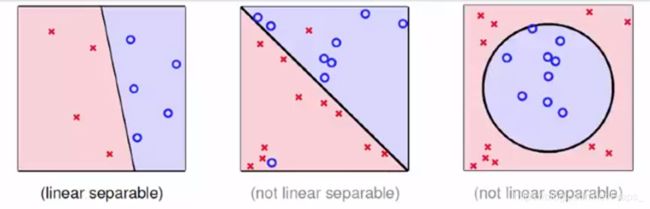
PLA算法只能在线性可分的情况下发挥作用!,那们在线性可分的数据集 D D D中,PLA中的可以找到一条线吗?
证明如下:
假 定 , W f 在 每 个 X n 出 都 能 正 确 划 分 , 所 以 有 : y n W f T x n > 0 在 P L A 第 T 轮 时 , 有 : y n ( t ) W f T x n ( t ) > 0 进 而 , 有 : y n ( t ) W f T x ≥ m i n n y n W f T x n > 0 对 于 其 中 的 一 轮 , 选 出 的 一 个 任 意 错 误 点 ( x n ( t ) , y n ( t ) ) W f T W t + 1 = W f T ( W t + y n ( t ) x n ( t ) ) ≥ W f T W t + m i n n y n W f T x n > W f T W t + 0. 假定,W_f在每个X_n出都能正确划分,所以有:\\ y_nW^T_fx_n >0\\ 在PLA第T轮时,有:\\ y_{n(t)}W^T_fx_{n(t)}>0\\ 进而,有:\\ y_{n(t)}W^T_fx \ge \mathop{\mathbb{min}}\limits_{n}y_nW^T_fx_n>0\\ 对于其中的一轮,选出的一个任意错误点(x_{n(t)},y_{n(t)})\\ \begin{aligned} W^T_fW_{t+1} &=W^T_f(W_t+y_{n(t)}x_{n(t)}) \\ &\ge W^T_fW_t+\mathop{\mathbb{min}}\limits_{n}y_nW^T_fx_n \\ &> W^T_fW_t+0. \end{aligned} 假定,Wf在每个Xn出都能正确划分,所以有:ynWfTxn>0在PLA第T轮时,有:yn(t)WfTxn(t)>0进而,有:yn(t)WfTx≥nminynWfTxn>0对于其中的一轮,选出的一个任意错误点(xn(t),yn(t))WfTWt+1=WfT(Wt+yn(t)xn(t))≥WfTWt+nminynWfTxn>WfTWt+0.
所以我们发现,每一轮更行, W f W t W_fW_t WfWt都在变大,内积变大,说明他们越来约靠近,说明算法确实在逼近最优的那条线,但是,目前的证明还不完整,他们值表达,还有可能时应为他们的模场增加。所以,继续证明:
根 据 P L A 算 法 , 我 们 知 道 , s i g n ( W t T x n ( t ) ) ⇔ y n ( t ) W t T x n ( t ) ≤ 0 ∣ ∣ W t + 1 ∣ ∣ 2 = ∣ ∣ W t + y n ( t ) x ( n ( t ) ) ∣ ∣ 2 = ∣ ∣ W t ∣ ∣ 2 + 2 y n ( t ) W n ( t ) T x n ( t ) + ∣ ∣ y n ( t ) x n ( t ) ∣ ∣ 2 我 们 知 道 P L A 只 有 在 “ 犯 错 ” 的 时 候 才 会 更 新 W , 同 时 2 y n ( t ) W n ( t ) T x n ( t ) ≤ 0 , 所 以 W 是 缓 慢 成 长 的 并 且 是 依 靠 ∣ ∣ y n ( t ) x n ( t ) ∣ ∣ 2 这 一 项 成 长 的 , 所 以 有 : ∣ ∣ W t + 1 ∣ ∣ 2 ≤ ∣ ∣ W t ∣ ∣ 2 + 0 + ∣ ∣ y n ( t ) x n ( t ) ∣ ∣ 2 ≤ ∣ ∣ W t ∣ ∣ 2 + m a x n ∣ ∣ y n x n ∣ ∣ 2 到 此 , 合 并 以 上 的 两 段 证 明 , 得 出 : W f t ∣ ∣ W f t ∣ ∣ W T ∣ ∣ W T ∣ ∣ ≥ T ⋅ a , a 是 一 个 常 数 . 到 此 , 我 们 知 道 了 P L A 算 法 确 实 是 使 得 W t 靠 近 最 由 的 那 个 W f . 根据PLA算法,我们知道,sign(W^T_tx_{n(t)}) \Leftrightarrow y_{n(t)}W^T_tx_{n(t)} \le 0 \\ \begin{aligned} ||W_{t+1}||^2 &= ||W_t+y_{n(t)x_(n(t))}||^2 \\ &=||W_t||^2+2y_{n(t)}W^T_{n(t)}x_{n(t)}+||y_{n(t)}x_{n(t)}||^2\\ \end{aligned}\\ 我们知道PLA只有在“犯错”的时候才会更新W,同时2y_{n(t)}W^T_{n(t)}x_{n(t)}\le0,\\ 所以W是缓慢成长的并且是依靠||y_{n(t)}x_{n(t)}||^2这一项成长的,所以有:\\ \begin{aligned} ||W_{t+1}||^2 &\le ||W_t||^2+0+ ||y_{n(t)}x_{n(t)}||^2\\ &\le ||W_t||^2+\mathop{\mathbb{max}}\limits_{n} ||y_nx_n||^2 \end{aligned}\\ 到此,合并以上的两段证明,得出:\\ \frac{W^t_f}{||W^t_f||}\frac{W_T}{||W_T||}\ge \sqrt{T}·a,a是一个常数.\\ 到此,我们知道了PLA算法确实是使得W_t靠近最由的那个W_f. 根据PLA算法,我们知道,sign(WtTxn(t))⇔yn(t)WtTxn(t)≤0∣∣Wt+1∣∣2=∣∣Wt+yn(t)x(n(t))∣∣2=∣∣Wt∣∣2+2yn(t)Wn(t)Txn(t)+∣∣yn(t)xn(t)∣∣2我们知道PLA只有在“犯错”的时候才会更新W,同时2yn(t)Wn(t)Txn(t)≤0,所以W是缓慢成长的并且是依靠∣∣yn(t)xn(t)∣∣2这一项成长的,所以有:∣∣Wt+1∣∣2≤∣∣Wt∣∣2+0+∣∣yn(t)xn(t)∣∣2≤∣∣Wt∣∣2+nmax∣∣ynxn∣∣2到此,合并以上的两段证明,得出:∣∣Wft∣∣Wft∣∣WT∣∣WT≥T⋅a,a是一个常数.到此,我们知道了PLA算法确实是使得Wt靠近最由的那个Wf.
最后组合哪里我还没有推出来
Non-Seqarable Data
思考:
- 在使用PLA时,数据集必须是线性可分的,但是,我们不可能事先知道一个陌生的数据集是否线性可分
- 及时数据集线性可分,如何知道PLA多久停下来
在真实的数据集中,是不免不了有干扰数据的。
Pocket Algorithm
修改PLA:

(附上最后汇总的推导)
https://www.cnblogs.com/HappyAngel/p/3456762.html
https://kelvin.ink/2018/06/10/ML2_PerceptronAlgorithm/
PLA python 实现
import numpy as np
import matplotlib.pyplot as plt
data = np.array(
[
[1,4],[1,5],[2,6],[3,5],[4,5],
[1,2],[1,1],[2,2],[3,3],[4,1],[5,3]
]
)
label=np.array(
[
-1,-1,-1,-1,-1,
1,1,1,1,1,1
]
)
plt.scatter(data[:5,0],data[:5,1],c='r')
plt.scatter(data[5:,0],data[5:,1],c='k')
W = np.zeros(len(data.shape)+1,dtype=np.float)
def pla(datas,labels):
count = 0
global W
datas=np.c_[datas,np.ones(len(datas))]
lines=[]
out = len(datas)
while True:
for i in range(len(datas)):
count =count+1
x = datas[i]
y = labels[i]
temp = np.dot(W, x)
compare = temp * y
if compare <= 0:
add = x * y
W = W + add
lines.append(W)
plt.scatter(data[:5, 0], data[:5, 1], c='r')
plt.scatter(data[5:, 0], data[5:, 1], c='k')
x = np.arange(0, 5)
W[1] =W[1] + 0.001 #divide zero
y = -W[0] / W[1] * x - W[2] / W[1]
plt.plot(x, y)
plt.xlim(0, 6)
plt.ylim(0, 7)
plt.savefig('IMAGE/plot{0}.png'.format(count), format='png')
plt.show()
break
if i+1 ==out :
break
return W, lines
permutation = np.random.permutation(data.shape[0])
shuffied_data = data[permutation]
shuffied_label = label[permutation]
W_n , lines= pla(shuffied_data,shuffied_label)
