（88）--Python数据分析：线性回归分析

# 线性回归分析

import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
from scipy import linalg
tita_list=[]
def upload_csv(name):
    array_data=np.loadtxt(fname=name,dtype=np.float64,delimiter=',')
    array_data_x=array_data[:,:array_data.shape[1]-1],array_data_y=array_data[:,array_data.shape-1]

    return array_data_x,array_data_y
def singel_predition(predition_point,Arrpara_x,Arrpara_y,k):
    X= np.column_stack((np.ones( Arrpara_x.shape[0]),Arrpara_x))
    #print(X)
    Y= Arrpara_y
    #print(Y)
    m = np.shape(X)[0]
    weights = np.identity(m)#生成单位矩阵
    for i in range(m):
        #print(predition_point,Arrpara_x[i])
        diff_all_points = predition_point - Arrpara_x[i]
        #print(diff_all_points)
        weights[i,i] = np.exp((diff_all_points**2)/(-2.0 * k**2)) # 权值计算和生成权值矩阵
        #print(weights[i,i])
    #print(weights)
    XWX = np.dot(X.T,np.dot(weights,X)) 
    #print(XWX)    #对x值进行加权计算          
    if linalg.det(XWX) == 0.0:
        #print('singular Matrix')
        return

    tita = np.dot(linalg.inv(XWX),np.dot(X.T,np.dot(weights,Y)))# 计算回归系数
    tita_list.append(tita)
    return np.dot (np.hstack((np.array([1]),np.array([predition_point]))),tita)#返回y值
#以上是对一个点的加权预测
    

def other_point_prediction(array_x,array_y,k):
    tita_list=[]
    m=np.shape(array_x)[0]
    null_array=np.zeros(m)
    for i in range(m):
        array_x_cor = np.delete(array_x,i,0)
        array_y_cor = np.delete(array_y,i,0)
        null_array[i]=singel_predition(array_x[i],array_x_cor,array_y_cor,k)
    return null_array

Data1=pd.read_csv(r'Desktop\bankloan.csv',delimiter=',')
del Data1['Unnamed: 9']
Data2=Data1.values
D_X=Data2[:501,4];
D_Y=Data2[:501,5]



from matplotlib.animation import FuncAnimation#引入函数动画、

import seaborn as sns#美化图形包

sns.set_style("whitegrid")

#设置图像主图风格（白色格子）
fig, ax = plt.subplots()
fig.set_tight_layout(True)#紧凑的布局

#单个作图
#tita_list=[]
DY_pre=other_point_prediction(D_X,D_Y,10)
DY_pre_pd=pd.Series(DY_pre)
DY_pre_pd[DY_pre_pd.isnull()]=0
DY_pre_pd
DY_Pre_ar=DY_pre_pd.values
#分别作图
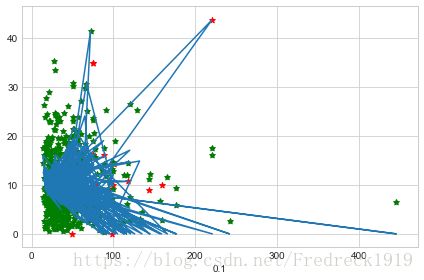
ax.scatter(D_X,D_Y,c='green',marker='*')
line=ax.plot(D_X,DY_Pre_ar)
plt.show()
for k in range(1,20,1):
    fig, ax = plt.subplots()
    fig.set_tight_layout(True)#紧凑的布局
    theory_y=other_point_prediction(D_X,D_Y,0.1*k)
    plt.scatter(D_X,D_Y,c='k',marker='.')
    plt.scatter(D_X,theory_y,c='r',marker='*')
    a=0.1*k
    ax.set_xlabel(a)
    #循环作图
    DY_pre=other_point_prediction(D_X,D_Y,k*0.2)
    DY_pre_pd=pd.Series(DY_pre)
    DY_pre_pd[DY_pre_pd.isnull()]=0
    DY_pre_pd
    DY_Pre_ar=DY_pre_pd.values
     #分别作图
    ax.scatter(D_X,D_Y,c='green',marker='*')
    Pre_image=ax.plot(D_X,DY_Pre_ar)
    
C:\ProgramData\Anaconda3\lib\site-packages\matplotlib\figure.py:1999: UserWarning: This figure includes Axes that are not compatible with tight_layout, so results might be incorrect.
  warnings.warn("This figure includes Axes that are not compatible "



D_XT=Data2[501:601,4]
D_YT=Data2[501:601,5]
#tita_list=[]
DY_pre=other_point_prediction(D_XT,D_YT,0.4)
DY_pre_pd=pd.Series(DY_pre)
DY_pre_pd[DY_pre_pd.isnull()]=0
DY_pre_pd
DY_Pre_ar=DY_pre_pd.values
Square_diff=np.sqrt(np.sum((DY_Pre_ar-D_YT)**2)/D_YT.shape[0])
Square_diff
Out[307]: 6.62889589872667#非常理想的值，测试通过
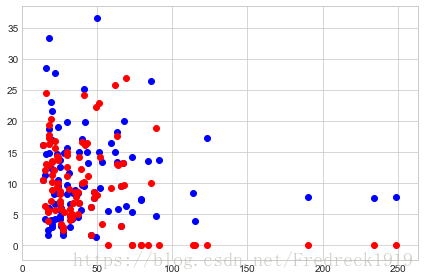
figt, axt= plt.subplots()
figt.set_tight_layout(True)

axt.scatter(D_XT,D_YT,c='b')
axt.scatter(D_XT,DY_Pre_ar,c='r')
plt.show()

C:\ProgramData\Anaconda3\lib\site-packages\matplotlib\figure.py:1999: UserWarning: This figure includes Axes that are not compatible with tight_layout, so results might be incorrect.
  warnings.warn("This figure includes Axes that are not compatible "

 DY_pre=other_point_prediction(Data2[0:601,4],Data2[0:601,5],0.4)
DY_pre_pd=pd.Series(DY_pre)
DY_pre_pd[DY_pre_pd.isnull()]=0
DY_pre_pd
DY_Pre_ar=DY_pre_pd.values
fig3, ax3 = plt.subplots()
fig3.set_tight_layout(True)
blist=[];klist=[]
for j in range(len(tita_list)):
    blist.append((tita_list[j])[0])
    klist.append((tita_list[j])[1])
b_array=np.array(blist);k_array=np.array(klist)
ax3.scatter(b_array,k_array,c='r',marker='.')

Out[4]: 

def ols_func(array_x,array_y):
   X= np.column_stack((np.ones(array_x.shape[0]),array_x))
   alpha=np.dot(linalg.inv(np.dot(X.T,X)),np.dot(X.T,array_y))
   return alpha


ols_func(b_array,k_array)

Out[5]: array([ 0.1176558 , -0.01211346])

fig4, ax4 = plt.subplots()
fig4.set_tight_layout(True)
KB_Vector=ols_func(b_array,k_array)
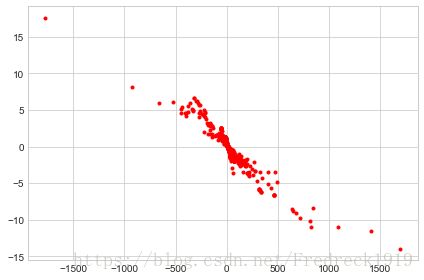
ax4.plot(b_array,KB_Vector[1]*b_array+KB_Vector[0],'r-')
ax4.scatter(b_array,k_array,c='b',marker='.')
plt.show()

C:\ProgramData\Anaconda3\lib\site-packages\matplotlib\figure.py:1999: UserWarning: This figure includes Axes that are not compatible with tight_layout, so results might be incorrect.
  warnings.warn("This figure includes Axes that are not compatible "





 tita_list=[]

DY_pre=other_point_prediction(Data2[0:601,4],Data2[0:601,5],0.4)
DY_pre_pd=pd.Series(DY_pre)
DY_pre_pd[DY_pre_pd.isnull()]=0
DY_pre_pd
DY_Pre_ar=DY_pre_pd.values
fig3, ax3 = plt.subplots()
fig3.set_tight_layout(True)
blist=[];klist=[]
for j in range(len(tita_list)):
    blist.append((tita_list[j])[0])
    klist.append((tita_list[j])[1])
b_array=np.array(blist);k_array=np.array(klist)
ax3.scatter(b_array,k_array,c='r',marker='.')

Out[7]: 

 def ols_func(array_x,array_y):
   X= np.column_stack((np.ones(array_x.shape[0]),array_x))
   alpha=np.dot(linalg.inv(np.dot(X.T,X)),np.dot(X.T,array_y))
   return alpha
#一般线性回归
ols_func(b_array,k_array)

Out[8]: array([ 0.09180041, -0.01217391])

fig4, ax4 = plt.subplots()
fig4.set_tight_layout(True)
KB_Vector=ols_func(b_array,k_array)
ax4.plot(b_array,KB_Vector[1]*b_array+KB_Vector[0],'r-')
ax4.scatter(b_array,k_array,c='b',marker='.')
plt.show()

C:\ProgramData\Anaconda3\lib\site-packages\matplotlib\figure.py:1999: UserWarning: This figure includes Axes that are not compatible with tight_layout, so results might be incorrect.
  warnings.warn("This figure includes Axes that are not compatible "





mintest_1=1000
trager=0
for j in range(b_array.shape[0]):
    min_test=abs(KB_Vector[1]*b_array[j]+KB_Vector[0]-k_array[j])
    if mintest_1>min_test:
        mintest_1=min_test
        trager=j
mintest_1,trager

Out[10]: (0.0010751752851243801, 558)

b_array[558]
Out[11]: 10.611459722418658

k_array[558]
Out[12]: -0.038457762731468392

(10.611459722418658-2.2)/10.611459722418658
Out[13]: 0.7926769683390406

 

兄弟连学python

Python学习交流、资源共享群：563626388 QQ