【机器学习笔记01】最小二乘法（一元线性回归模型）

【参考资料】
【1】《概率论与数理统计》
【2】 http://scikit-learn.org /stable/auto_examples/ linear_model/ plot_ols.html # sphx-glr-auto-examples-linear-model-plot-ols-py

---

数学基础

1. 基本定义：
随机变量Y（因变量）和变量X（自变量）之间存在某种关系。假设随机变量Y的期望存在且是X的函数$\mu =\mu (x)$,这里$\mu (x)$称为Y关于X的回归函数，简称Y关于X的回归。

如上图所表示，如果$\mu =\mu (x)$满足$a+bx$的形式，可以如下定义一元线性回归模型：

$$\{\begin{array}{l}y=a+bx+\epsilon \\ \epsilon \sim N(0,{\sigma }^2)\end{array}$$
备注：相当于一个线性的模型上叠加了一个方差很小的正态分布误差

2. 推导过程

已知$Y_i\sim N(a+b{X}_i,{\sigma }^2)$,由于$Y_i$独立，因此根据极大似然估计法，构建联合分布密度函数如下：

$$L=\prod _{i=1}^n\frac{1}{\sigma \sqrt{2\pi }}exp[-\frac{1}{2{\sigma }^2}(y_i-a-b{x}_i{)}^2]$$

上式取最大值，等价于$Q(a,b)=(y_i-a-b{x}_i{)}^2$取最小值，因此对其求偏导数

$$\{\begin{array}{l}\frac{\partial Q}{\partial a}=-2\sum _{i=1}^n(y_i-a-b{x}_i)=0\\ \frac{\partial Q}{\partial b}=-2\sum _{i=1}^n(y_i-a-b{x}_i)x_i=0\end{array}$$
上式1两边同时除-2n,上式2两边除-2，且替换$n\bar{x}=\sum _{i=1}^n{x}_i$
$$\{\begin{array}{l}a+b\bar{x}=\bar{y}\\ n\bar{x}a+\sum _{i=1}^n{x}_i^{2}b=\sum _{i=1}^n{x}_i{y}_i\end{array}$$
求解上述方程可以得到b,a的最大似然估计值如下：
$$\{\begin{array}{l}\hat{b}=\frac{\sum x_i{y}_i-n\bar{x}\bar{y}}{\sum _{i=1}^n{x}_i^2-n{\bar{x}}^2}\\ \hat{a}=\bar{y}-\hat{b}\bar{x}\end{array}$$

---

程序实现 (基于sklearn)

# -*- coding: utf-8 -*-
import numpy  as np
import matplotlib.pyplot as plt
from sklearn import linear_model


def _test_one_lr():

    index  = np.linspace(0, 10, 20);

    x_test = np.hstack((index, np.ones(20))).reshape(2,20)

    """
    随机变量为y = 0.3x + 0.2 + delta
    从矩阵的角度看y = wx
    w = [0.3,0.2]^T x = [x, 1]^T
    """
    delta  = np.random.random_sample(20)

    y_test = 0.3*index + 0.2*np.ones(20) + delta

    regr = linear_model.LinearRegression()

    """
    输入时转置，由行矩阵变成列矩阵
    fit方法为进行模型训练
    """
    regr.fit(np.transpose(x_test),np.transpose(y_test))

    """
    根据训练得到的模型进行预测
    """
    y_pred = regr.predict(np.transpose(x_test))

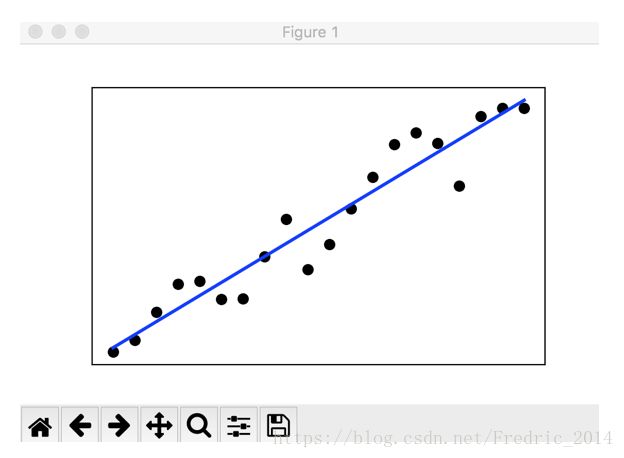
    plt.scatter(index, y_test,  color='black')
    plt.plot(index, y_pred, color='blue', linewidth=2)

    plt.xticks(())
    plt.yticks(())

    plt.show()


if __name__ == "__main__":

    _test_one_lr()

输出结果：

---

程序实现 (使用极大似然估计公式推导)

# -*- coding: utf-8 -*-
import numpy  as np
import matplotlib.pyplot as plt 



def _test_one_lr(): 

    index  = np.linspace(0, 10, 20);

    """
    随机变量为y = 0.3x + 0.2 + delta
    从矩阵的角度看y = wx
    w = [0.3, 0.2]^T x = [x, 1]^T

    delta 是一个混淆变量
    """
    delta  = np.random.random_sample(20)/10

    y_test = 0.3*index + 0.2*np.ones(20) + delta


    x_mean = np.mean(index)
    y_mean = np.mean(y_test)

    b_up   = np.dot(index, y_test) - 20 * x_mean * y_mean

    b_down = np.dot(index, index) - 20 * x_mean * x_mean

    b = b_up / b_down

    a = y_mean - (b * x_mean)

    
    print("function: y =  (%f) * x + %f" %(b, a))

    #输出: function: y =  (0.300204) * x + 0.252471

"""
说明：

一元线性回归的最小二乘法实现，采用极大似然估计的概率公式。对应的笔记《最小二乘法（一元线性回归）》

作者：fredric

日期：2018-8-11

"""
if __name__ == "__main__":

    _test_one_lr()